10.3.4. Дененің ауырлық кіндігі координаталары мен инерциялық моменттері.

,

(10.46)

,

денесінің массасы,

, ,

- сәйкес , , координаталық жазықтықтарға қарағандағы дененің статикалық моменттері деп аталады.

Егер беттік тығыздығы параметрлері арқылы өрнектеліп, функциясы арқылы берілген беттің статикалық моменттері:

,

;

,

. (10.47)

бетінің массасы.

; ; (10.48)

.

(10.49)

,

, (10.50)

.

М.16*. Біртекті жарты шардың ауырлық кіндігі координаталарын табайық.

Шешуі. Алдымен жазықтықтарына сәйкес статикалық моменттерін есептейік. Ол үшін декарттық координаталар жүйесінен сфералық жүйеге көшеміз. Ол кезде, екендігін көреміз. Сонымен,

,

,

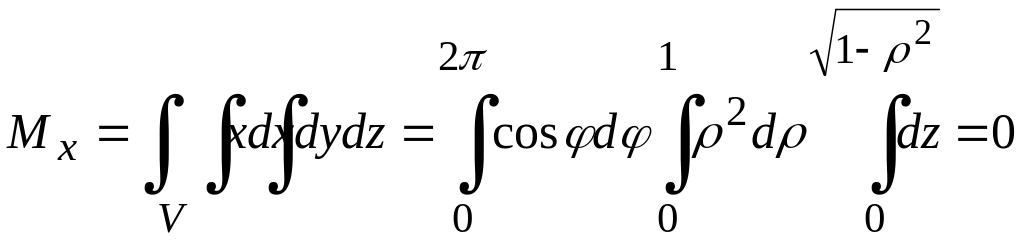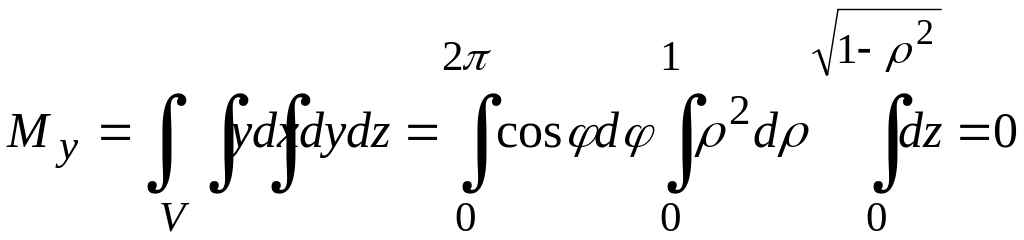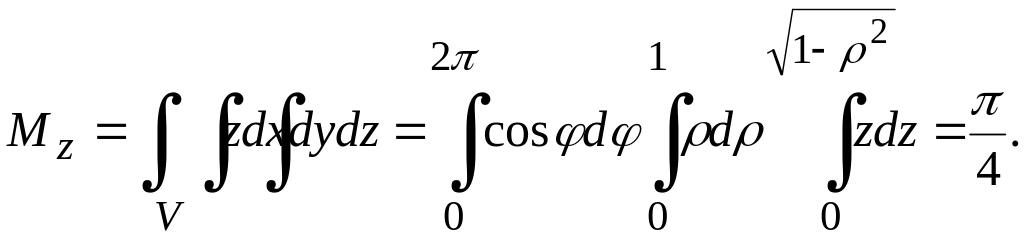
Дененің тығыздығы болғандықтан . Демек, (10.46) формула бойынша, дененің ауырлық кіндігі координаталары:

§10.4 Еселі меншіксіз интегралдар

10.4.1. Шектелмеген функциялардың интегралдары.

Функцияның аймағы бойынша екі еселі меншіксіз интеграл деп,

ш егін айтамыз.

Е гер де бұл шек бар және ол шек ақырлы болса, онда меншіксіз интеграл жинақты, егер де шек жоқ болса – интеграл жинақсыз деп

аталады. Ал интегралы жинақты болса, меншіксіз

интеграл абсолютті жинақты деп аталады. Демек, кез келген абсолютті жинақты еселі меншіксіз интеграл жинақты болады. Ескерту. Бір айнымалы функциялардағы меншіксіз интеграл мен еселі меншіксіз интегралдардың қасиеттері ортақ. Сондықтан тек салыстыру белгісін келтірейік.

1 0.4.2. Шектелмеген аймақ бойынша меншіксіз интегралдар.

С онымен, шектелмеген интегралдау аймағы бойынша меншіксіз интгерал деп, тізбегін қалайша алуымыздан тәуелсіз болатын

шегін айтамыз.

М. 17*. а)

ә )

б)

в)

г)

интегралдарын сәйкес аймақтары бойынша жинақтылыққа зерттейік.

Ш ешуі. а) Берілген функциясы бас нүктеде шексіздікке айналады. Сондықтан осы нүктенің d-маңайын

ойып алып, берілген интегралды аймақтың қалған бөлігі (ойық дөңгелек) бойынша есептейік. Интегралды алу үшін біріншіден, полярлық координаталарға көшейік, екіншіден, жоғарыдағы (10.51) анықтаманы пайдаланамыз. Сонымен,

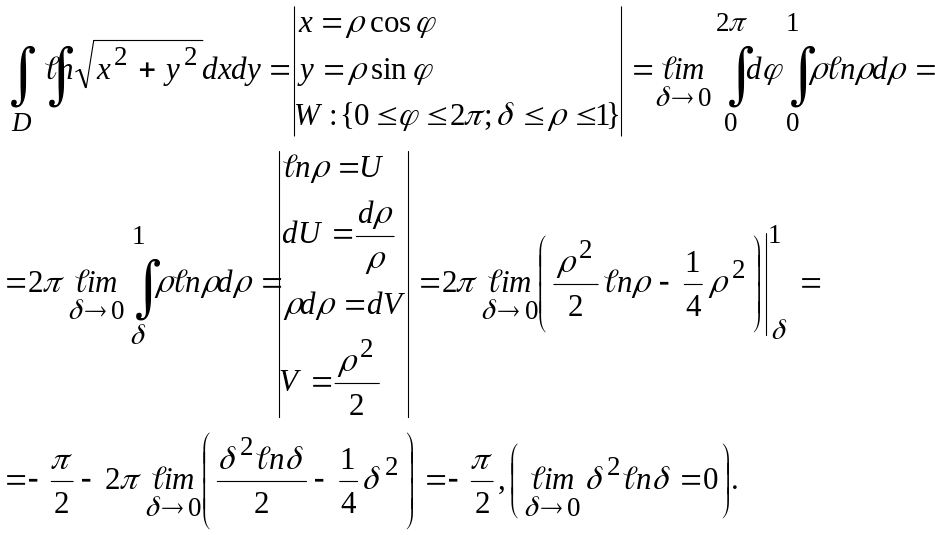
? Демек, берілген интеграл жинақты.

ә) Берілген интегралды ойық дөңгелекте қарастырамыз. Тағы да полярлық координаталарға көшеміз

С онымен,

интегралы a<2 болғанда жинақты, a³2 – жинақсыз.Бұл интегралда сфералық координаталар жүйесіне көшу арқылы зерттейік.

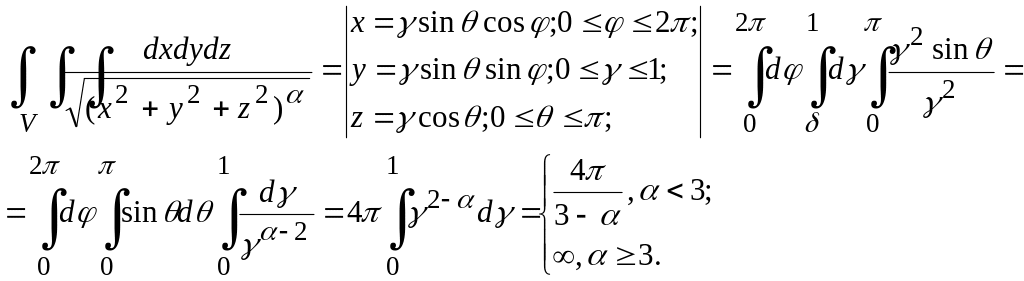
Берілген интеграл a<3 болғанда жинақты, a³3 жинақсыз.

в ) Интегралдау аймағы барлық жазықтығын алып жатыр. Сондықтан интегралдау аймақтары D_n, n=1, ретінде берілген D

а ймағын толық қамтитын радиусы n-ге тең дөңгелектер

т ізбегін қарастырамыз. Тағы да полярлық координаталарға көшу арқылы.

Б ерілген интеграл жинақты.

Б арлық жазықтығы бойынша алынған еселі интегралды қайталанбалы интегралға келтіру арқылы есептеуге немесе зерттеуге болады, яғни

2)

болғандықтан, (10.54) теңдікті пайдаланамыз.

Е ндеше,