10. Еселі интегралдар
М.1*.
интегралын
–
тік төрт бұрышы бойынша есептейік.
Шешуі.
–
тік
төрт бұрыш қабырғалары бойынша екі
еселі интегралдың төменгі және жоғарғы
шектерін қоямыз:
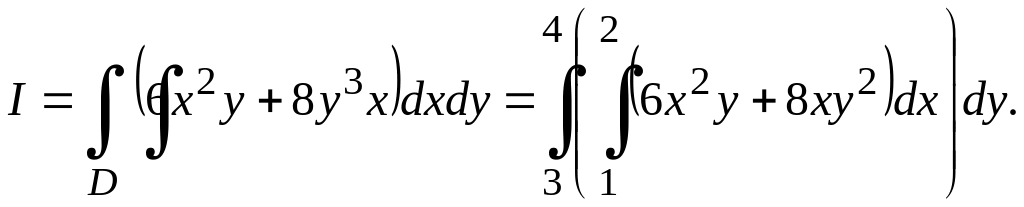
Енді
уақытша
айнымалысын тұрақты ретінде қабылдап,
ішкі интегралды
бойынша
интегралдаймыз. Соңынан, екінші интегралды
екінші айнымалы
бойынша
интегралдаймыз. Сонымен,
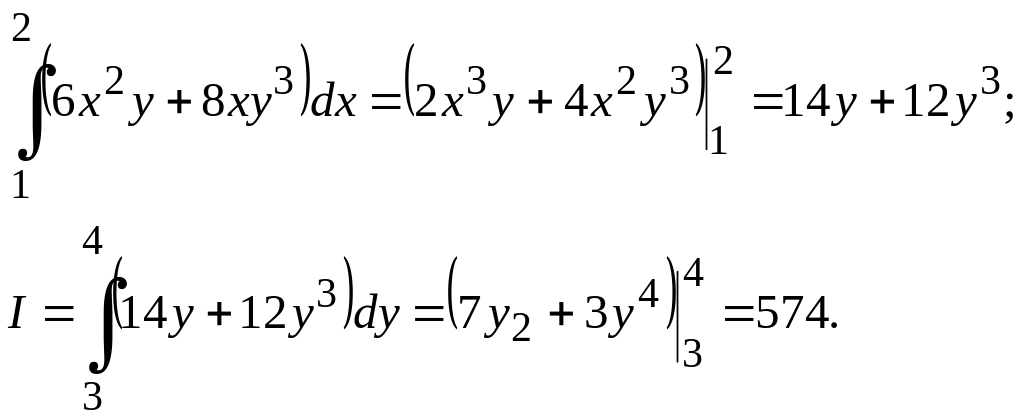
Енді интегралдау ретін өзгертіп берілген интегралды есептейік.
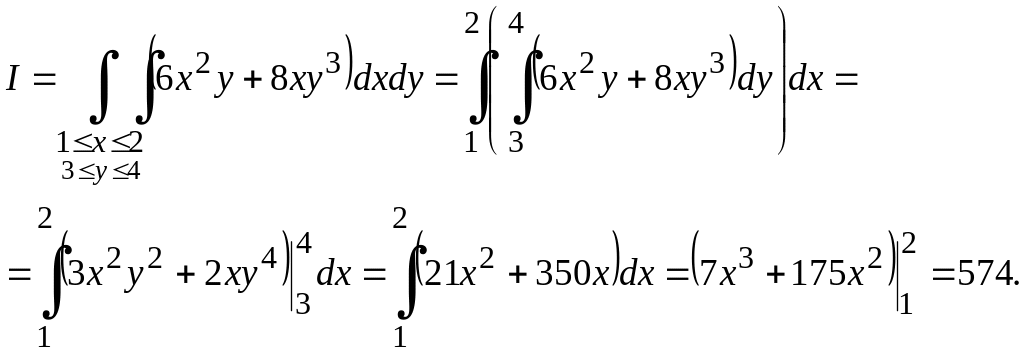
М.2*.
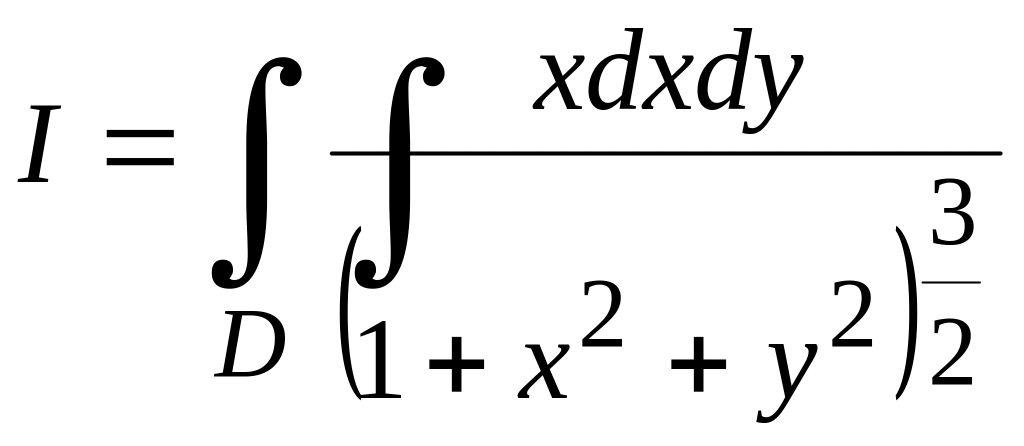интегралын
тік төрт бұрышы бойынша есептейік.
Шешуі. Кей интегралды есептеу үшін алдымен қай айнымалыны бірінші, қайсысын екінші ретке қоюды анықтау басты мәселе болады. Сондықтан да, интеграл астындағы өрнекке көңіл аудару қажет. Берілген интегралды алу үшін алдымен бойынша алған дұрыс екендігі бірден көзге ілінеді. Сонымен,
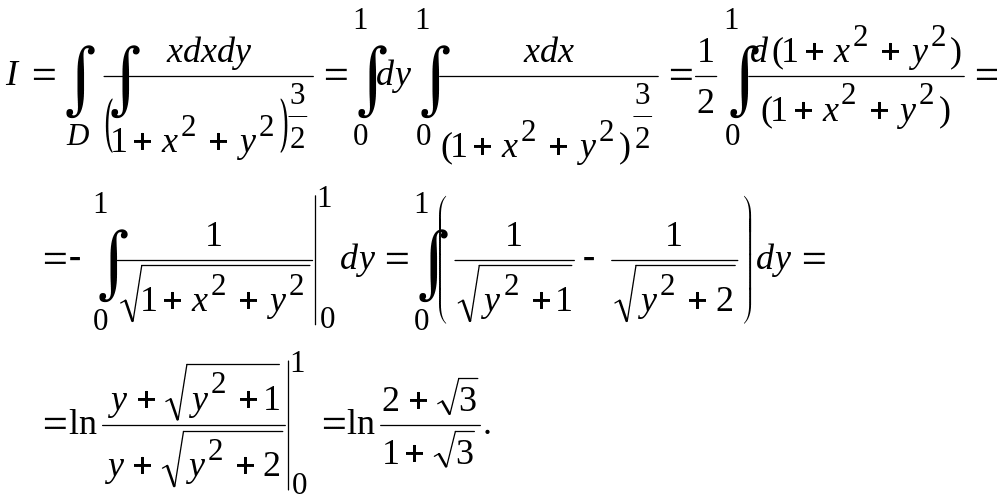
2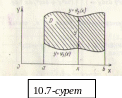
°.
Қисық
сызықты аймақ бойынша есептеу.
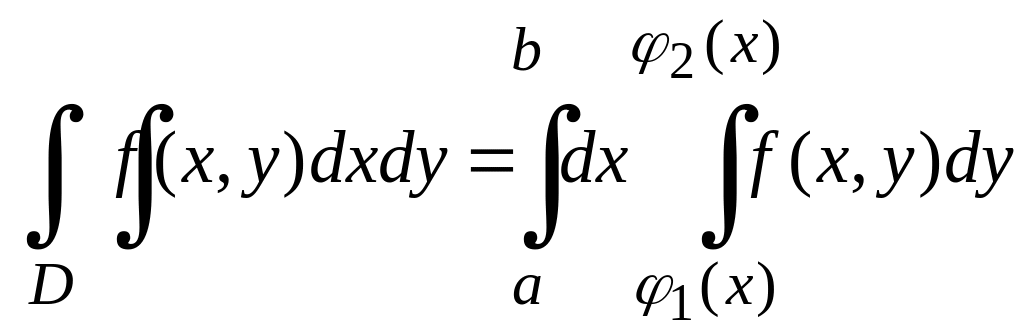(10.9)
М.3*.
интегралын
аймағы бойынша есептейік (10.8-сурет).
Шешуі.
Келтірілген 10.8-суреттегі
аймағы бойынша (10.9) формуланы пайдаланып,
берілген интегралды оңай есептеуге
болады.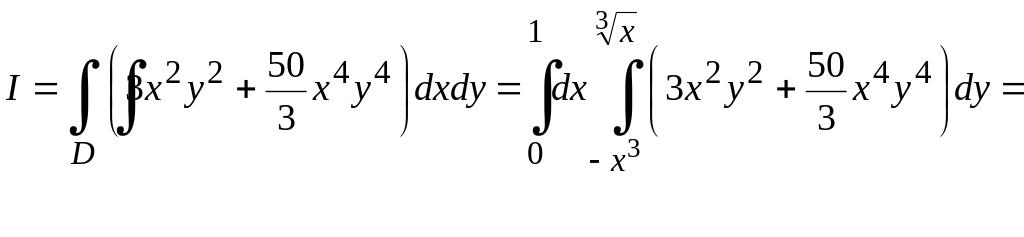 
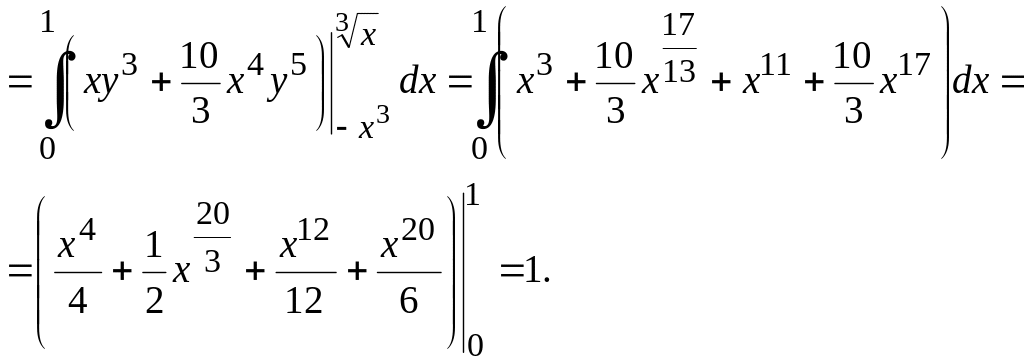
М.4*.
интегралын
аймағы
бойынша есептейік Шешуі.
Жоғарыдағы (10.10) формуланы пайдаланамыз.
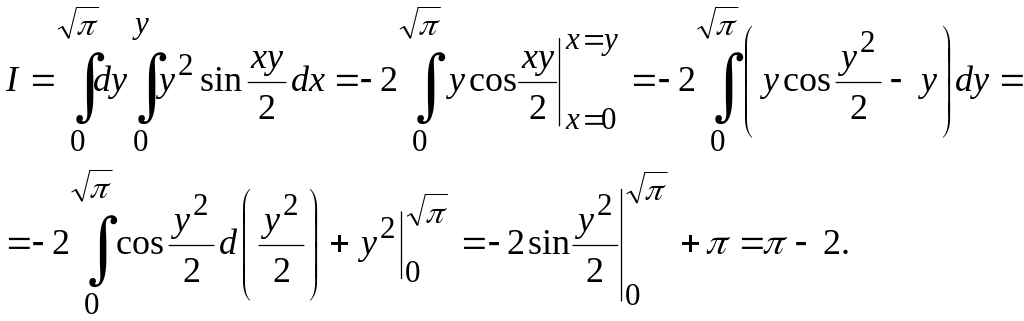
М.5*. Төменде берілген интегралдар қосындысының интегралдау бағыттарын, яғни интегралдау ретін өзгертейік
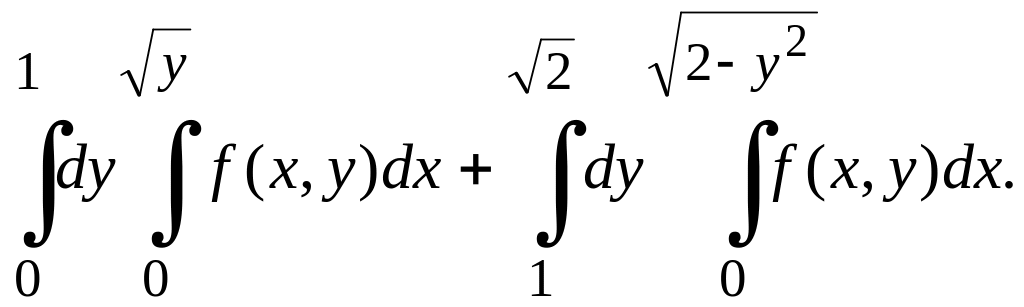
Ш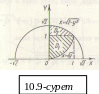
ешуі.
Алдымен берілген интегралдың төменгі
және жоғарғы шектерін пайдалану арқылы
жалпы
аймағын анықтап алғанымыз жөн. Сонымен,
бірінші интегралдан:
ал екінші интегралдан
екендігін көреміз.
Демек,
төменнен
парабола үзігімен, жоғарыдан шеңбердің
бөлігімен, ал
болатындығын көреміз (10.9-сурет).
Ендеше, (10.9) формула бойынша:
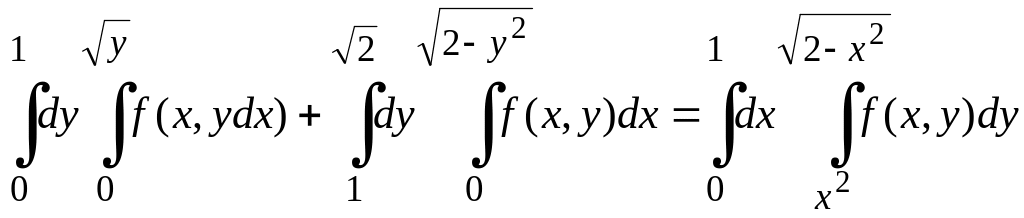
теңдігін аламыз. Ал теңдіктің дұрыстығын 10.5-теорема айқындайды.
10.1.6. Үш еселі интеграл.
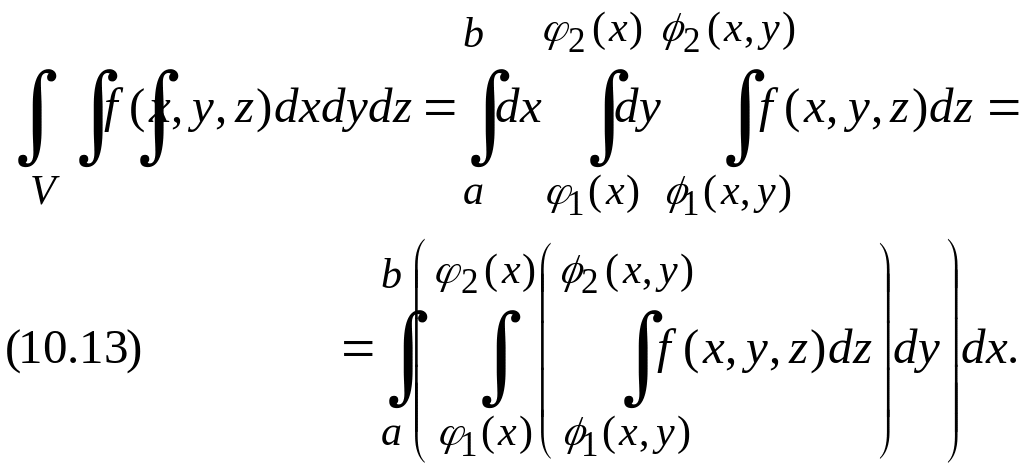
Демек,
алдымен
ті
уақытша тұрақты ете тұрып,
айнымалысы бойынша ішкі интеграл
алынады. Одан
ті
тұрақты деп алып,
айнымалысы
бойынша екінші интеграл, ең соңында,
соңғы үшінші интеграл қалған
бойынша
алынады.
М.6*.
интегралын төменде берілген аймақ (
бойынша
есептейік.
Ш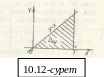
ешуі.
денесі төменнен
жазықтығымен, жоғарыдан
элипстік параболойдпен шектелген
дененің Оху
жазықтығына
проекциясы
үш бұрыш болып шығады (10.12-сурет).
Демек, (10.13) формула бойынша,
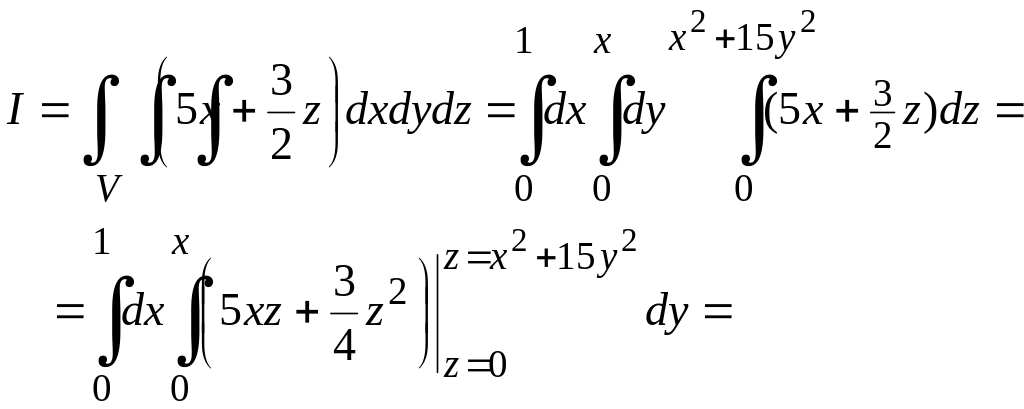
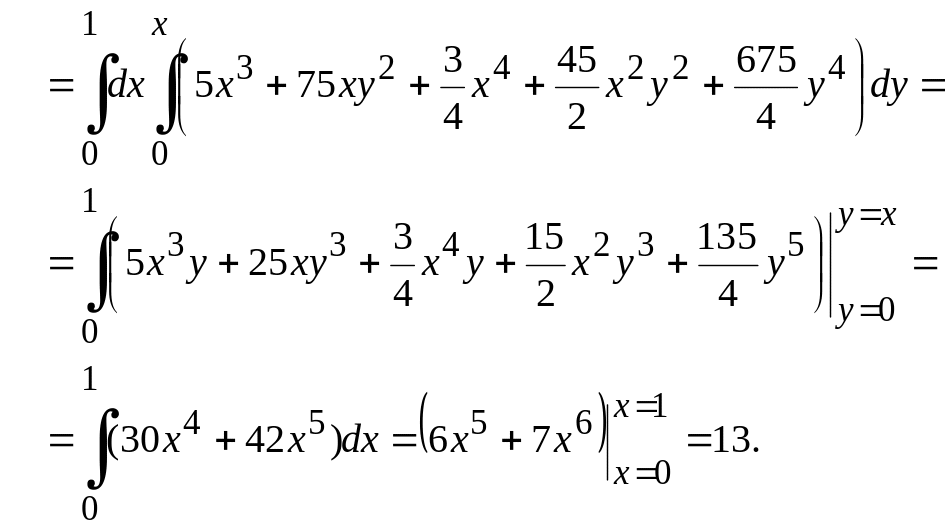
Ескерту.
Кез келген (мысал үшін,
еселі) интеграл үшін жоғарыдағы
келтірілген мәселелерді қайталау керек.
Сондықтан да, оларды келтірудің қажеті
жоқ деп білеміз. Тек қана,
еселі
интеграл үшін
кеңістігі бойынша алынады да, интеграл
түрінде жазылып ары қарай рет-ретімен есептеліне береді.
§ 10.2. Еселі интегралдарда айнымалыларды ауыстыру
10.2.2. Екі еселі интегралда айнымалыларды ауыстыру.
Көпшілік
жағдайда, екі еселі интегралдарда
айнымалыларды ауыстыру негізінен
полярлық координаталарға
ге
көшу жиі қолданылады. Полярлық
координаталар мен тік бұрышты координаталар
жүйелері арасындағы байланыс:
теңдіктері арқылы жүзеге асырылады.
Мұндағы:
Полярлық координаталар жүйесіндегі
координаттық сызықтар ретінде, кіндігі
бас нүктеде жататын осы нүктеден шығатын
сәуленің
болғандағы концентрлік шеңберлер
қарастырылады.
Жоғарыдағы
(10.16) формулаға сәйкес
деп алсақ,
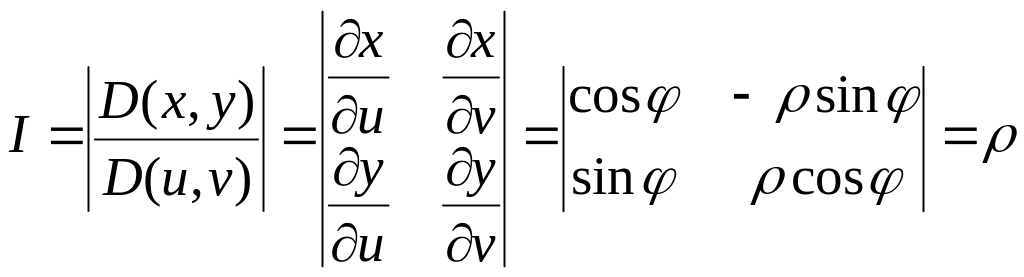(10.17)
болатындығы белгілі. Ендеше, (10.17) – якобианды пайдаланып, екі еселі интегралдың полярлық координаталарға көшкендегі түрін аламыз:
(10.18)
Ал аймағының полярлық координаталар арқылы алынған ауданы
(10.19)
теңдігімен өрнектеледі.
Полярлық координаталар жүйесінің жалпыланған түрі мына түрде жазылады:
Бұдан
радиандық координата
болса, онда полярлық координаталардың
жалпы түрі
жарты өстері
және
болатын эллипсті береді. Бұл жағдайда
якобиан –
болады да, екі еселі интеграл жаңа
айнымалылыр бойынша
(10.20)
болып шығады.
Бірнеше мысалдар қарастырайық.
М.17*.
Мына
сызықтарымен шектелген фигураның
ауданын есептейік.
Шешуі. Алғашқы теңдеулерді толық квадратқа дейін толықтырайық:
(1)
– кіндіктері
және
нүктелерінде
жататын, радиустары сәйкес
болатын шеңберлер.
Енді
берілген теңдеулерде полярлық
координаталарға көшейік,
болғанда
(2)
Демек,
(3)
Ендеше, (1), (2), (3) теңдіктерді ескере отырып және (10.19) формула бойынша
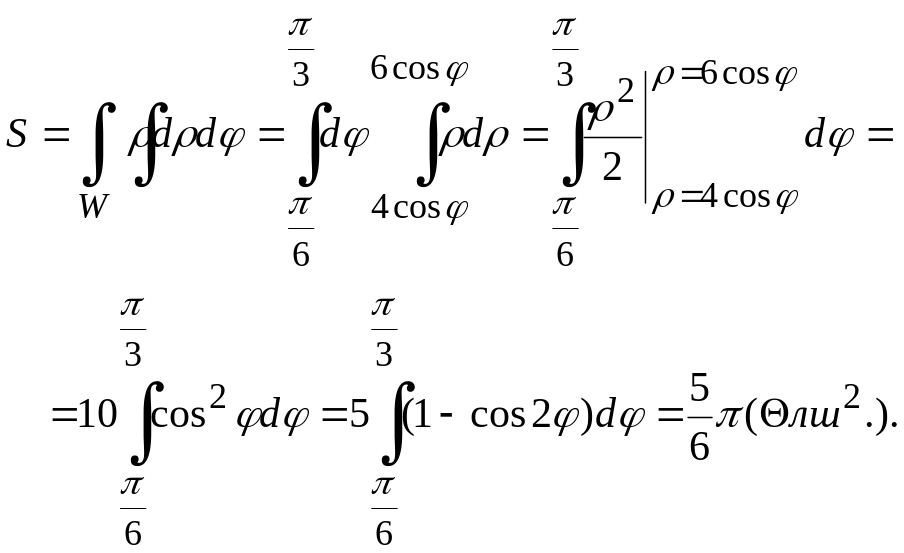
М
.8*.
Беттік тығыздығы
болатын,
теңдеулерімен шектелген сақина бөлігінің
(10.15-сурет)
массасын есептейік.
Шешуі. Жоғарыда келтірілген (10.20) формула бойынша ізделініп отырған сақинаның массасы
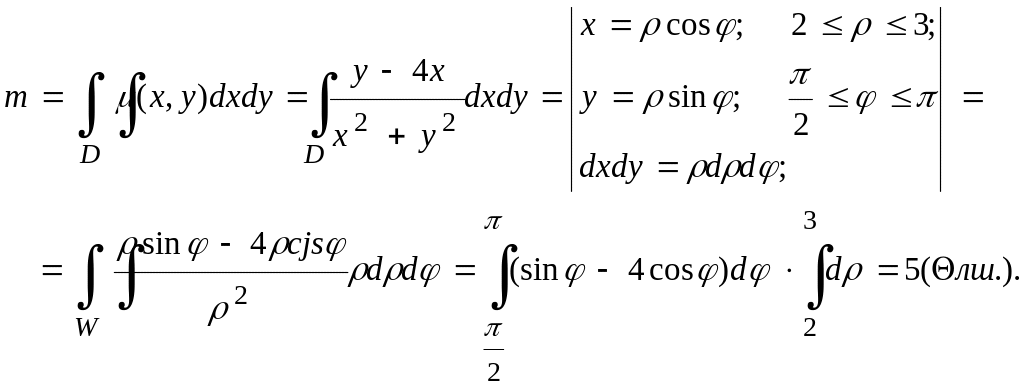
М.9*.
Беттік тығыздығы
болатын,
табақшасының
массасын есептейік.
Шешуі.
Бұл мысалда жалпыланған полярлық
координаталар жүйесіне көшеміз, яғни
Онда якобиан
Енді
берілген теңсіздіктерді пайдаланып
радиальдық радиус пен полярлық бұрыштың
өзгеру аралығын табамыз. Сонымен,
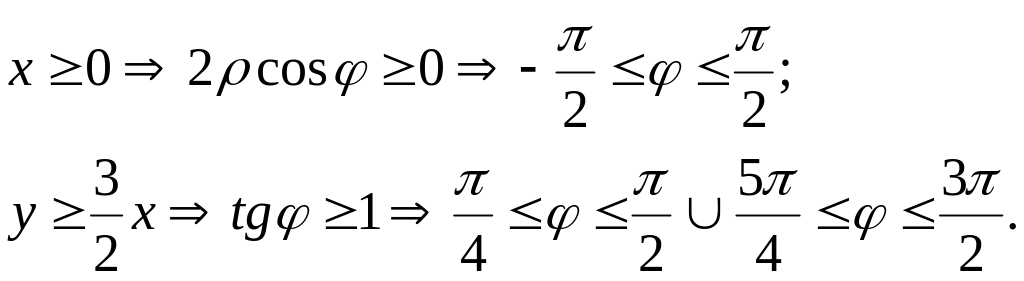
Демек,
бәріне ортақ
Ендеше, (10.20) формула бойынша,
