2. Дәрежелік қатардың жинақталу аймағы.
Енді
жинақталу радиусын табу жолдарын
қарастырайық. Ол үшін негізінде өзімізге
белгілі Д’Аламбер және Коши белгілерін
пайдаланылады. Ол үшін белгілі бір
үшін
қатарын қарастырайық. Айталық,
немесе
(11.30)
ақырлы шегі бар болсын. Онда
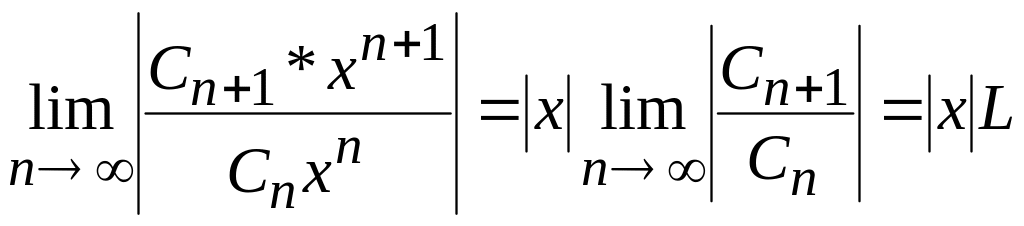
болатындығы
белгілі. Ендеше, Д’Аламбер белгісі
бойынша (11.28) қатар
болғанда жинақты және
болғанда ─
жинақсыз болады.
Егер
.
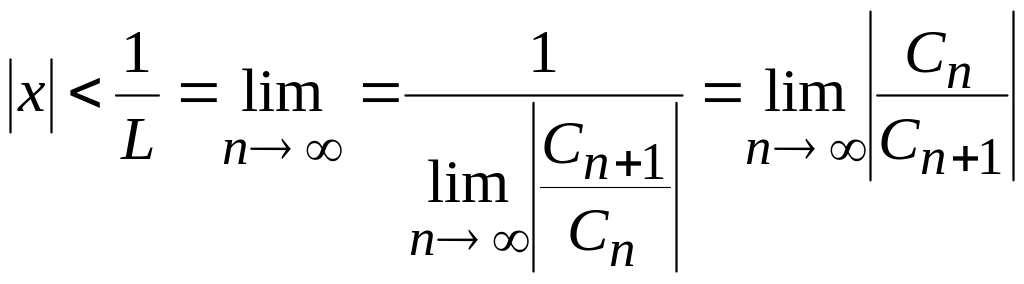Ара
қатынасы орындалатын болса, онда (11.28)
дәрежелік орындалатын болса, онда
(11.28) дәрежелік қатар жинақты болады да,
болады – қатар жинақсыз болады,
Сонымен, қатарының жинақталу радиусы
немесе
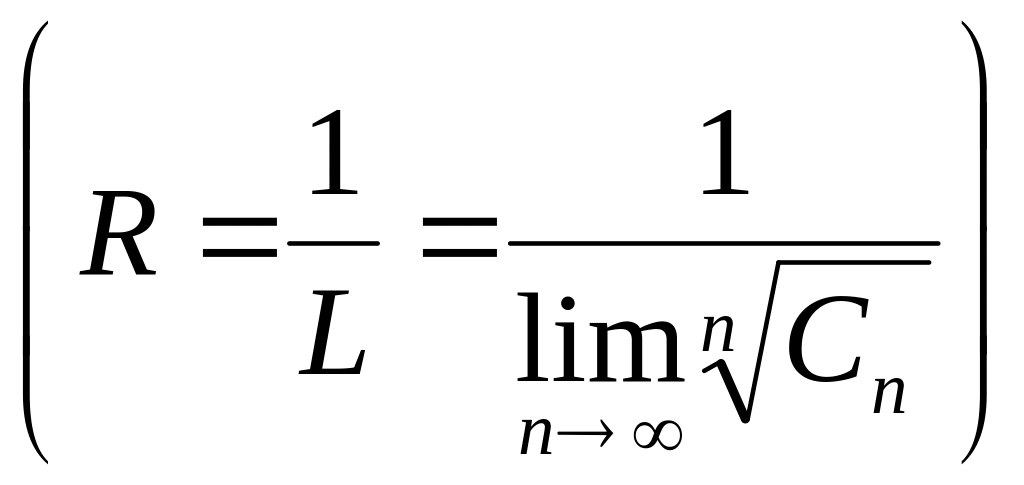(11.31)
формуласы бойынша табылады. Жақша ішіндегі өрнек Коши-Адамар) формуласы деп аталады. Ендеше,
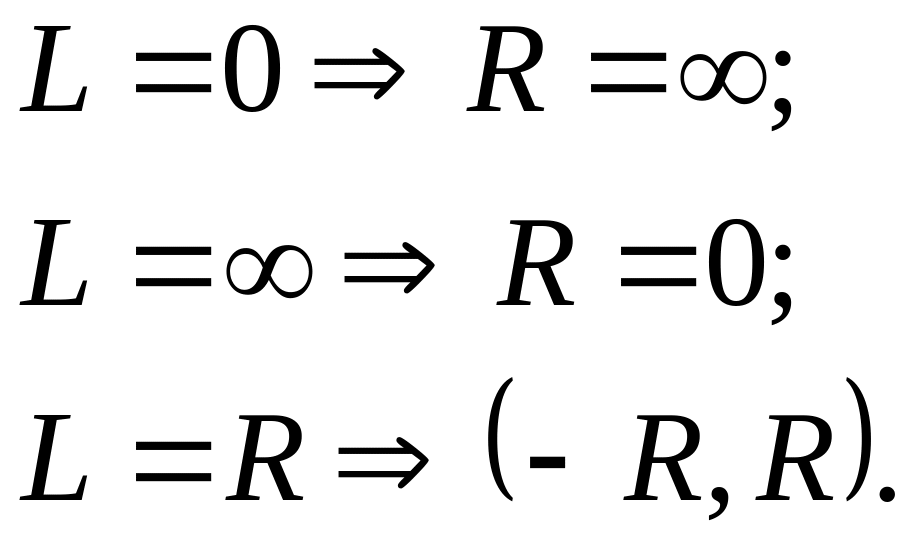
М.19*.
а)
,
ә)
қатарлары үшін жинақталу радиустарын
табайық.
Шешуі. Жоғарыда келтірілген (11.31) формулаларды пайдаланайық, яғни
а)
.
ә)
.
Демек,
бірінші дәрежелік қатардың жинақталу
аралығы (-1, 1) болады, ал
болғанда
жинақсыз. Ал екінші қатардың жинақталу
аймағы (-2, 2) аралығы болса,
болғанда жинақсыз болады.
Ендігі мақсат шеткі нүктелерін тексеру.
а)
Айталық,
─
жинақты бигармоникалық қатар,
─
абсолютті жинақты қатар.
ә)
Айталық,
─
жинақсыз;
─
шартты жинақты қатар аламыз,
Сонымен,
берілген бірінші қатар:
кесіндісінде
жинақты, ал екінші
...................................................................
*) Ж, Адамар (1865 – 1963) – француз математигі
қатар
жарты
аралықта ғана жинақты болады.
М. 20*.
қатарының жинақталу аймағын табайық.
Шешуі. Жоғарыдағы (11.31) формула бойынша,
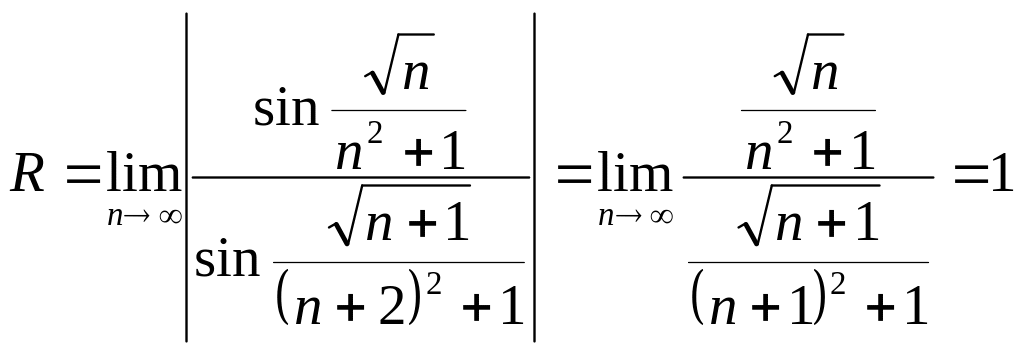
Демек,
берілген қатардың жинақталу аймағы
(-1,1). Ендеше,
.
Онда қатар
және
болғанда жинақсыз болады,
Енді шеткі нүктелерді зерттейік:
шартты
жинақты;
─ абсолютті
жинақты. Онда берілген қатардың жинақталу
аймағы
кесіндісі
болып шығады.
Ескерту.
Есте
болатын жағдай ─
ақырлы шек бар, яғни
дәрежелік қатардағы
-тің
барлық дәрежелік қатысқан кезде (11.31)
формуланы қолдану дұрыс жолға келтіріледі.
Ал дәрежелік қатардағы
-тің
кейбір дәрежелері қатыспайтын болса,
; 
.
Ендеше, (11.31) формуланы қолдануға болмайды. Мұндай кездері, өзімізге белгілі Д`Аламбер белгісін тікелей қолданған жөн, яғни
.
Демек,
қарастырылған қатар
болғанда жинақты болады.
М.21*.
дәрежелік қатарының қосындысын табайық.
Шешуі. Алдымен жинақталу радиусын табайық.
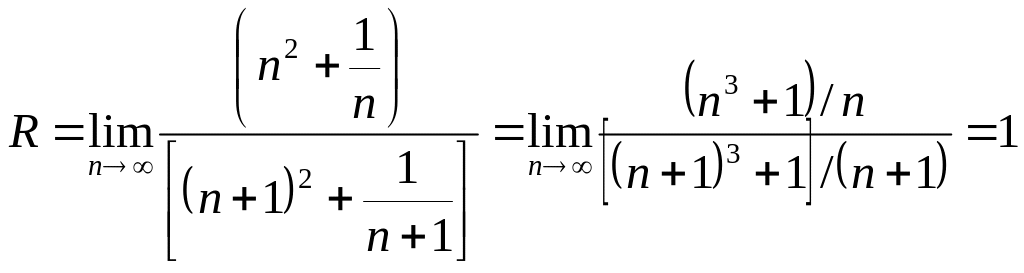
Енді берілген қатарды түрлендірейік
Мұндағы
,
.
Онда
.
Жинақталу аймағы
болғандықтан,
болады. Ендеше
Бұдан
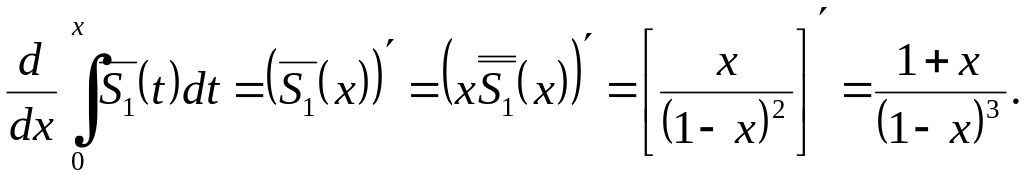
Сонымен,
Онда
Бұдан
Ал
.
Демек,
ақырында
болғанда
.