5.6. Рекомендации по определению показателей унификации и стандартизации

Стандартизация и унификация предусматривает рациональное сокращение количества типоразмеров составных частей в проектируемых и изготовляемых изделиях.

Уровень стандартизации и унификации изделия характеризуется конкретными числовыми показателями (коэффициенты применяемости и повторяемости).

Коэффициент применяемости характеризует степень насыщенности изделия стандартизированными составными частями. Различают коэффициент применяемости по типоразмерам и коэффициент применяемости по составным частям изделия.

Коэффициент применяемости по типоразмерам (К_пр) определяют по формуле:

, (68)

где П – общее количество типоразмеров составных частей в изделии;

П₀ – количество типоразмеров оригинальных составных частей в изделии.

П= П_ст + П_у + П₀, (69)

где П_ст – количество типоразмеров стандартизированных составных частей;

П_у – количество типоразмеров унифицированных составных частей.

Коэффициент применяемости по типоразмерам стандартизированных составных частей (К_пр.ст) определяется по формуле:

, (70)

Коэффициент применяемости по типоразмерам унифицированных составных частей (К_пр.у) определяется по формуле:

, (71)

Коэффициент применяемости по составным частям изделия (К_пр.сч) определяется по формуле:

, (72)

где N – общее количество составных частей, входящих в изделие;

– количество оригинальных составных частей.

N = N_ст + N_у + N₀ (73)

где N_ст – количество стандартизированных составных частей;

N_у - количество унифицированных составных частей.

Коэффициент применяемости по стандартизированным составным частям ( ) определяется по формуле:

, (74)

Коэффициент применяемости по унифицированным составным частям ( ) определяется по формуле:

, (75)

Коэффициент повторяемости (К_п) характеризует степень унификации составных частей в изделии.

, (76)

где N – общее количество составных частей, входящих в изделие;

– общее количество типоразмеров составных частей в изделии.

5.7. Задачи для решения

Задача 5.7.1.

В таблице 5.9 представлены данные по вариантам о составных частях двух изделий.

На основании этих данных рассчитать и произвести сравнение:

- коэффициентов применяемости по типоразмерам;

- коэффициентов применяемости по составным частям изделия;

- коэффициентов применяемости по типоразмерам стандартизирован­ных составных частей;

- коэффициентов применяемости по типоразмерам унифицированных составных частей;

- коэффициентов применяемости по стандартизированным составным частям;

- коэффициентов применяемости по унифицированным составным частям;

- коэффициентов повторяемости.

Результаты расчетов следует оформить по образцу приложения 2.

Таблица 5.9 – Исходные данные к задаче 5.7.1

№ п/п	Наименование показателей	Варианты
		1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10	11	12
	Изделие А
1	Количество типоразмеров составных частей, шт.
1.1	стандартизированных	18	19	20	21	22	23	24	25	30	40
1.2	унифицированных	22	21	22	23	24	25	26	27	32	20
1.3	оригинальных	2	3	4	5	6	7	8	9	8	2
2	Количество составных частей, шт.
2.1	стандартизированных	80	79	80	81	82	84	85	86	106	120
2.2	унифицированных	28	29	30	32	33	35	36	37	49	50
2.3	оригинальных	2	3	4	6	8	9	8	9	10	5
	Изделие Б
1	Количество типоразмеров составных частей, шт.
	стандартизированных	20	21	22	23	26	28	29	30	40	50
	унифицированных	22	23	25	26	28	23	24	25	28	20
	оригинальных	3	3	4	5	8	7	8	9	10	5
2	Количество составных частей, шт.
2.1	стандартизированных	78	78	79	80	85	87	88	90	101	100
2.2	унифицированных	32	30	29	30	32	38	40	42	43	40
2.3	оригинальных	3	3	4	5	10	9	10	12	12	5

6. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ

6.1. Рекомендации по разработке сетевых графиков

При построении сетевого графика следует придерживаться следующих правил:

Правило 1. Каждая работа в сети обязательно должна иметь начальное и конечное события. Два любых события могут быть прямо связаны только одной работой.

Правило 2. Каждое событие в сети, за исключением исходного и завершающего, обязательно должно иметь не менее одной предшествующей ему работы и не менее одной последующей ему работы.

Правило 3. Ни одна работа не может быть начата, пока не наступит момент свершения ее начального события. Событие свершится только тогда, когда все предшествующие ему работы будут выполнены.

Несоблюдение этих трех правил приводит к тому, что в сети появляются «висячие события», т.е. такие события, в которые не входит ни одна работа (кроме исходного) и из которых не исходит ни одна работа (кроме завершающего). Например, на рис. 6.1 события Б и К.

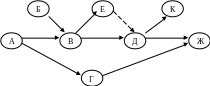
Рисунок 6.1 –«Висячие» события сетевого графика

Наличие «висячих» событий требует дополнительного анализа: являются ли работы, соединяющие эти события с сетью необходимыми для достижения конечной цели выполняемого комплекса работ; не опущены ли при построении модели какие-либо работы, предшествующие этим событиям или следующие за ними.

Правило 4. Для изображения одновременных или параллельных работ, имеющих одни и те же начальные и конечные события, необходимо с целью сохранения однозначности работ между событиями ввести дополнительные события и фиктивные работы. Число вводимых событий и фиктивных работ равно числу параллельных работ минус единица. Это правило можно проиллюстрировать на рис. 6.2, где изображение а), заменяется либо изображением б), либо изображением в).

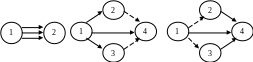
а) б) в)

Рисунок 6.2 - Изображение параллельно выполняемых работ.

Правило 5. Для изображения различной зависимости некоторых последующих работ от некоторых предшествующих работ, объединяемых одним событием, необходимо ввести дополнительные события и фиктивные работы.

Правило иллюстрируется тремя примерами (рис. 6.3., 6.4, 6.5).

На рис. 6.3 а) работы 3-4 и 3-6 не могут быть начаты, пока не будут выполнены предшествующие им работы 1-3 и 2-3. Но может быть так, что работа 3-6 зависит от них, а работа 3-4 не зависит от работы 2-3. В этом случае построение участка сети необходимо выполнить так, как показано на рис. 6.3 б).

Для рис. 6.4 а) требуется выполнить условия: работа 5-8 зависит от работ 2-5 и 3-5 и не зависит от работ 4-5; работа 5-9 зависит от работ 3-5 и 4-5 и не зависит от работы 2-5. В этом случае построение участка необходимо выполнить так, как показано на рис. 6.4 б).

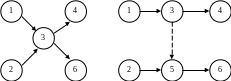
а) б)

Рисунок 6.3.

а) б)

Рисунок 6.4 - Изображение дифференцированно зависимых работ.

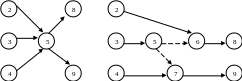
Для рис. 6.5 а) требуется выполнить условия: работа 6-8 зависит от работ 2-6 и 3-6; работа 6-7 зависит от работы 2-6 и не зависит от работы 3-6; работа 6-9 зависит от работы 3-6 и не зависит от работы 2-6. Построение участка для этого случая показано на рис. 6.5 б), где введение фиктивных работ 5-6 и 4-6 позволяет выполнить требуемое условие. Легко проверить, что устранение одной из фиктивных работ уже не будет удовлетворять условиям задачи.

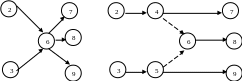
а) б)

Рисунок 6.5 - Изображение дифференцированно зависимых работ.

Правило 6. В сетевом графике не должно быть замкнутых контуров (петель), т.е. таких последовательностей работ, двигаясь по которым возвращаются снова к тому же самому событию, из которого начато движение. Например, на рис. 6.6. работы а), б) и в) образуют петлю.

а

в б

Рисунок 6.6

Правило 7. При разработке сетевого графика следует стремиться к тому, чтобы сеть имела простую компактную форму без лишних пересечений стрелок, чтобы все соответствующие ее работы имели одинаковое направление. Общепринято выдерживать направление слева направо.

Продолжительность каждой работы ( _i-j) и дисперсия (_{t i-j}) определяются по формулам:

, (77)

, (78)

где t_min – минимальное время выполнения работы;

t_н.в – наиболее вероятное время выполнение работы;

t_max – максимальное время выполнения работы.