2.9. Игры с ограничениями
Рассмотрим игру, в которой допускаются не все смешанные страте-
гии. Обычно для этого имеются определѐнные практические основания.
Предположим, что смешанные стратегии x и y соответственно должны
выбираться из некоторых выпуклых многогранников.
Если матрица игры A ={aij}, то задача игрока 1 состоит в том, чтобы
найти
max{min xAy T } ,
x X y Y
где два множества X и Y определяются соответственно неравенствами
(1)
xB
C,
и
x
yE T
0
F ,
y 0.
Аналогично задача 2-го игрока состоит в том, чтобы найти
min{max xAy T }
y Y x X
(2)
при тех же ограничениях на стратегии игроков.
В выражении (1) величина в скобках, очевидно, является функцией
x . Точнее она является значением задачи линейного программирования,
целевая функция которой имеет коэффициенты, зависящие от x . По тео-
ремам двойственности, если эта задача допустима и ограничена, то две за-
дачи
min xAyT
y
T
(3)
y 0,
40
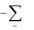
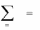
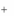
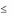
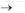
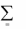
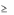
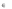
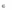
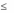
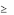
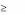
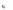
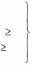
yE F ,
и двойственная к ней
max zF T
z
zE
z
xA,
0
(4)
будут иметь одно и то же значение целевой функции. Значит, задача игро-
ка 1 сводится просто к задаче максимизации
max zF T
zE xA 0,
(5)
xB c ,
z, x 0.
Аналогично, можно показать, что задача (2) игрока 2 сводится к за-
даче минимизации:
min CsT
sBT
yE T
yAT
F ,
0, .
(6)
s, y 0.
Задачи (5) и (6) являются двойственными друг к другу. Если эти за-
дачи допустимы, то выражения (1) и (2) будут равны и, таким образом, иг-
ра с ограничениями будет иметь решение в смешанных стратегиях.
2.10. Бесконечные игры
Рассмотрим в первую очередь игры со счѐтным множеством страте-
гий. Пусть, как и в конечных играх aij – выигрыш, получаемый 1-м игро-
ком, при условии, что он выбирает i-ю чистую стратегию, а 2-й игрок, j-ю
чистую стратегию.
Смешанной стратегией игрока 1 будет последовательность ( x1 , x 2 ,
…), для которой
i 1
xi
1,
(1)
xi
0 .
(2)
Смешанная стратегия игрока 2 – ( y1 , y 2 , …).
Функция выигрыша при смешанных стратегиях ( x , y )
41
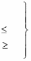
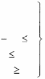
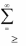
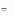
A( x, y)
xi aij y j
(3)
i 1 j 1
при условии, что ряд абсолютно сходится.
Игры со счѐтным множеством стратегий обладают рядом нежела-
тельных свойств, которых нет у конечных игр. Во-первых, ряд (3) не обя-
зательно сходится и может случиться, что
и
i 1 j 1
xi aij y j
xi aij y j
(4)
(5)
j 1 i 1
существуют, но различны. Во-вторых, множества смешанных стратегий не
компактны и, таким образом, максимумы и минимумы не будут существо-
вать.