2.7. Теорема о минимаксе
Для любой функции F (x, y) , определенной на произвольном декар-
товом произведении X
Y , имеет место неравенство
max min F (x, y)
x X y Y
Отсюда следует, что v1
v2 .
min max F (x, y)
y Y x X
(1)
Нижний выигрыш игрока 1 не может превышать верхнего проигры-
ша игрока 2.
Теорема о минимаксе утверждает, что v1
v2 .
31
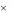
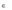
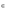
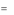
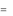
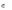
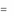
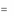
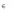
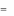
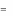
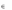
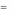
где A – j-й столбец матрицы А.
Эта важнейшая теорема доказана многими способами. Используем
доказательство фон Неймана и Моргенштерна. Для доказательства теоре-
мы рассмотрим сначала две леммы.
Лемма1. (Теорема об опорной гиперплоскости) Пусть B – замкнутое вы-
пуклое множество в n-мерном евклидовом пространстве, а x
( x1,..., xn ) –
некоторая точка, не принадлежащая B . Тогда существуют такие числа
p1, ..., pn , pn 1 , что
n
pi xi
pn
1
(2)
i 1
и
n
pi yi
pn 1 ,
y
B .
(3)
i 1
Геометрически это означает, что через точку x можно провести ги-
перплоскость так, что B будет лежать целиком «выше» этой гиперплоско-
сти.
Доказательство. Пусть z – такая точка из B , расстояние которой от x
минимально (такая точка существует, т.к. B замкнуто). Положим
pi
zi
n
xi , i 1, n ,
n
pn
1
i 1
zi xi
i 1
xi2 .
Очевидно, что равенство (2) выполняется, поскольку
n
n
n
i 1
(zi
xi )xi
i 1
zi xi
i 1
xi2
pn 1 .
Необходимо показать, что имеет место (3). Мы имеем
n
n
n
i 1
pi zi
i 1
z
2
i
i 1
zi xi
и, следовательно,
n
n
n
n
n
pi zi
pn
1
z
2
i
2
zi xi
2
i
(zi
xi ) 2
0 .
i 1
i 1
i 1
i 1
i 1
Поэтому
n
i 1
pi zi
pn 1 .
Допустим, что существует y
n
B , для которого
pi yi
pn 1 .
i 1
32
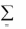
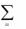
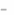
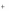
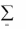
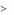
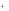
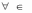
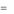
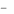
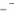
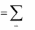
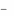
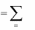
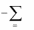
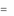
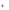
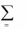
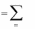
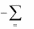
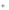
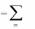
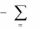
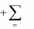
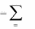
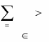
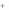
x
Так как B выпукло, то отрезок, соединяющий y с z , должен цели-
ком содержаться в B , т.е. точки этого отрезка
wr
ry (1 r)z B ,
0 r 1.
Квадрат расстояния от x до wr имеет вид
n
2
(x, wr )
(xi
ryi
(1 r)zi ) 2 .
i 1
Поэтому
2
n
r
2
i 1
( zi
yi )( xi
ryi
(1 r) zi )
n
n
n
2
( zi
xi ) yi
2
( zi
xi ) zi
2
r( zi
yi ) 2
i 1
n
n
i 1
n
i 1
2
pi yi
2
pi zi
2r
( zi
yi ) 2 .
i 1
i 1
i 1
При r
0 (то есть, при wr
z ) имеем
2
n
n
r
|r
0
2
i 1
pi yi
2
i 1
pi zi .
Здесь первое слагаемое по предположению не превосходит 2 pn 1 , а
2
второе больше 2 pn 1 . Поэтому |r 0 0 .
r
Отсюда следует, что для r , достаточно близких к нулю
( x, wr )
( x, z) .
Но это противоречит выбору z . Следовательно, для любых y
B
условие (3) должно выполняться.
Лемма 2. (Теорема об альтернативах для матриц). Пусть A {aij} , матрица
m n . Тогда справедливо либо утверждение 1, либо утверждение 2.
1. Точка 0 (в m-мерном пространстве) содержится в выпуклой оболочке m
+ n точек
a1
(a11 ,..., am1)
………………
и
an
e1
e2
(a1n ,..., amn )
(1,0,...,0) ,
(0,1,...,0) ,
………………
em
(0,0,...,1) .
2. Существуют числа x1,..., xm , удовлетворяющие условиям
33
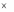
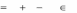
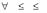
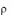
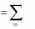
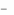
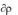
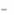
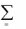
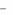
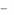
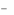
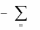
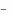
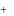
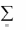
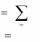
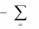
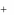
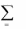
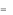
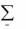
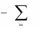
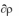
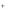
m
m
xi
0 ,
xi
1,
aij xi
0 , j 1, n .
i 1
i 1
Доказательство. Предположим, что 1 неверно. То есть, точка 0 не
содержится в выпуклой оболочке этих m + n точек.
На основании леммы 1 существуют такие числа p1, ..., pm 1 , что
m
i 1
0 pi
m
pm 1 .
Отсюда следует, что pm
1
0 и
pi yi
0 для всех y в указанном вы-
i 1
пуклом множестве. В частности это выполняется, если y является любым
из m+n векторов a j , ei . Поэтому
m
i 1
aij pi
0
j, j 1, n ,
pi
0
i,i 1, m .
Так как pi
0 , получаем
m
pi
0 , и можно положить xi
pi
m
.
m
i 1
m
i 1
pi
Следовательно,
aij xi
0 , xi
0 ,
xi
1.
Лемма доказана.
i 1
i 1
Доказательство теоремы о минимаксе ( v1
Это соответствует тому, что max min xA j
x X j
v2 )
min max Ai yT , где A j –
y Y i
столбец, а Ai – строка матрицы A .
Доказательство. Пусть A – матричная игра. По лемме 2 имеет место либо
утверждение (1), либо утверждение (2).
Если верно (1), то 0 является выпуклой линейной комбинацией m+n
векторов. Поэтому существуют такие S1 , …, S m n , что
m n
S j aij
Sn
i
0, i 1,..., m,
j 1
m n
S j
0,
j 1,..., m n;
S j
1.
j 1
34
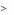
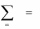
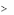
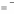
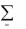
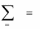
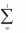
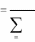
Если бы все числа S1 , …, S n были равны нулю, то 0 оказывался бы
выпуклой линейной комбинацией m единичных векторов e1 , e2 ,…, em ,
что, очевидно, невозможно, т.к. они линейно независимы. Следовательно,
n
по крайней мере, одно из чисел S1 , …, S n положительно и
j 1
S j
0.
Тогда можно положить y j
S j
n
,
S j
j 1
и мы получаем
y j
0,
n
j 1
y j
1,
n
aij y j
j 1
n
S n i
S j
0,
i.
j 1
Значит, v( y)
max Ai yT
0 и v2
0.
i
Предположим теперь, что верно утверждение (2):
xi
0,
m
i 1
xi
1,
m
i 1
aij xi
0,
j 1, n .
Тогда, v(x)
min xA j
j
min xAy T
y Y
0, так что v1
0.
Следовательно, неравенство v1
0
v2 не может иметь места.
Предположим теперь, что мы изменили игру А, заменив еѐ на игру
B {bij} , где bij
aij
k .
Ясно, что для любых x , y xBy T
xAy T
k. Поэтому
Так как неравенство
v1 (B)
v2 (B)
v1 ( A) k,
v2 ( A) k.
v1 (B)
0
v2 (B)
не может иметь места, то неравенство
v1 ( A)
k
v2 ( A)
также не выполняется. Но k – произвольно. Значит, неравенство v1
v2 не-
возможно. Так как v1
v2 , то
v1
v2 ,
что и требовалось доказать.
35
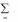
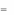
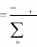
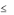
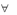
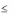
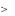
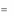
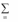
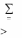
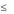
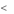
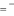
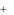
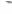
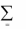
Таким образом, мы видим, что при использовании смешанных стра-
тегий нижний выигрыш игрока 1 в точности равен верхнему проигрышу
игрока 2. Общая величина V этих двух чисел называется значением игры.
Мы видим, что стратегия x , удовлетворяющая условию
m
xi aij
v,
j 1,2,..., n,
(4)
i 1
является оптимальной для игрока 1 в том смысле, что не существует стра-
тегии, которая дала бы ему больший ожидаемый выигрыш, чем v , против
каждой стратегии игрока 2.
Обратно, если y удовлетворяет условию
n
aij y j
v,
j 1, m,
(5)
j 1
то y является оптимальной для игрока 2 в том же смысле.
Далее, очевидно, что xAy T
v , т.к. если бы правая часть этого ра-
венства была меньше левой, то это противоречило бы (5), а если бы она
была больше левой – это противоречило бы (4). Следовательно, оптималь-
ные стратегии x и y являются также оптимальными одна против другой, а
также против любой иной оптимальной стратегии.
Будем называть любую пару оптимальных стратегий ( x , y ) – реше-
нием игры.