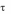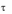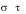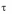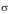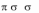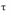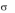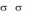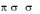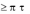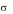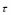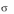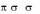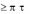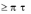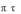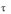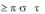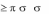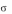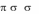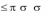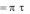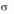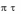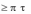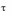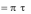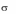2.3. Ситуации равновесия
Определение. Пусть дана игра Г. Говорят, что ситуация (т.е. какой-нибудь
n-набор стратегий) ( x1*,..., xi *,..., xn*) равновесна, или, что она является
26
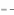
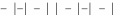
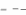
(0, 0) |
(−1/2, 1/2) |
(−1/2, 1/2) |
(0, 0) |
(1/2, −1/2) |
(0, 0) |
(0, 0) |
(1/2, −1/2) |
(1/2, −1/2) |
(0, 0) |
(0, 0) |
(1/2, −1/2) |
(0, 0) |
(−1/2, 1/2) |
(−1/2, 1/2) |
(0, 0) |
(−1, 1) |
(1, −1) |
(1, −1) |
(−1, 1) |
ситуацией равновесия, если для любого i
1, n и для любого xi
i
имеет
место неравенство
i
( x1*,..., xi 1*, xˆi , xi 1*,..., xn *)
i
( x1*,..., xi *,..., xn *) .
Другими словами – ситуация равновесна, если не один игрок не име-
ет никаких разумных оснований для изменения своей стратегии при усло-
вии, что все остальные игроки собираются придерживаться своих страте-
гий. В этом случае, если каждый игрок знает, как будут играть остальные,
он имеет основания придерживаться той стратегии, которая соответствует
этой ситуации равновесия. Тем самым игра становится весьма устойчивой.
Пример 2.4. Для игры в нормальной форме
1
2
1
2
(2,1)
(0,0)
(0,0)
(1,2)
как (
1
,
1
) , так и (
2
,
2
) являются ситуациями равновесия.
К сожалению, не каждая игра обладает ситуациями равновесия. На-
пример, игра в ―Орлянку‖ такой ситуации не имеет.
―Р‖
―О‖
―Р‖
―О‖
Вообще говоря, если игра не имеет ситуаций равновесия, то обычно
некоторые игроки пытаются отгадать стратегии остальных игроков, сохра-
няя собственные стратегии в тайне. Это наводит на мысль, что в играх с
полной информацией ситуации равновесия существуют (в конечных иг-
рах).
Действительно, справедлива следующая теорема:
Теорема: Любая конечная игра n лиц с полной информацией имеет
ситуацию равновесия.
2.4. Антагонистические игры. Игры с нулевой суммой
Определение. Игра называется игрой с нулевой суммой, если в каждой
окончательной позиции функция выигрыша ( p1, p2 , ... , pn ) , где pi – выиг-
рыш i-го игрока в этой позиции, удовлетворяет условию:
n
pi
0 .
(1)
i 1
27
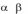
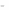
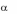
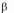
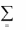
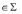
(−1, 1) |
(1, −1) |
(1, −1) |
(−1, 1) |
Вообще говоря, игра с нулевой суммой представляет собой замкну-
тую систему: все то, что кто-нибудь выиграл, должно быть кем-то проиг-
рано.
Игры двух лиц с нулевой суммой называются антагонистическими,
или строго конкурентными.
В случаях антагонистической игры можно просто задавать первую
компоненту вектора выигрышей, тогда вторая компонента равна первой с
противоположным знаком. Т.е. первая компонента называется просто вы-
игрышем, это означает, что второй игрок отдает эту сумму первому.
В антагонистических играх нет никаких оснований для переговоров
между игроками, так как если один выигрывает, то другой проигрывает.
Этим антагонистические игры отличаются ото всех остальных.
Теорема: Пусть ( 1, 2 ) и ( 1, 2 ) – две ситуации равновесия антагонис-
тической игры. Тогда
1) ( 1, 2 ) и ( 1, 2 ) также являются ситуациями равновесия и
2) ( 1, 2 )
( 1, 2 )
( 1, 2 )
( 1, 2 ) .
(2)
Доказательство. Ситуация
( 1, 2 )
равновесна. Следовательно
( 1, 2 )
( 1, 2 ) . Т.е. выбор любой другой стратегии первым игроком,
при условии, что второй сохранит стратегию
2 , приводит к худшему ре-
зультату.
С другой стороны, ситуация ( 1, 2 ) также равновесна. Поэтому
( 1,
2
)
( 1,
2
) . Т.е., так как ситуация равновесна, то выбранная вто-
рым игроком стратегия
2 увеличивает его проигрыш (следовательно уве-
личивается выигрыш первого). Таким образом
( 1, 2 )
( 1, 2 )
( 1, 2 ) .
Но, аналогично получится, если отправляться от ситуации ( 1, 2 ) :
( 1, 2 )
( 1, 2 )
( 1, 2 ) .
Из этих двух систем неравенств следует справедливость утверждения (2).
Далее, для любого ˆ 1
и для любого ˆ 2
( ˆ 1, 2 )
( 1, ˆ 2 )
( 1, 2 )
( 1, 2 )
( 1, 2 )
( 1, 2 ) .
Следовательно, ( 1 , 2 ) является ситуацией равновесия. Аналогично, рав-
новесна и ситуация ( 1 , 2 ) .
Эта теорема не имеет места для других игр (т.е., только для антаго-
нистических игр с нулевой суммой).
28
