5.2 Аналіз якості обслуговування телефонних викликів повнодоступною

комутаційною системою (КС) з очікуванням

Завдання:

1. При заданих значеннях інтенсивності навантаження (Y) і кількістю ліній (V) визначити ймовірність очікування р(γ>0). Побудувати сукупність графіків р(γ>0)=Dv(Y)=f(V) по розрахунках в п.5.2.1.

2. Визначити ефективність використання однієї лінії у=Y/V для заданих інтенсивності навантаження (Y) і втратах р(γ >0).

3. Визначити залежність ефективності використання однієї лінії від кількості ліній в пучку при заданих втратах (р =5% i р=10%).

Таблиця 1 - Вихідні дані

Дані	У, Ерл	У9лін
№ вар.
	Y= 5	V=5,6, 8,10
І	Y=10	V=10, 12, 14,16
	Y= 20	V=20,22,24,26
II	Y= 15	V=16, 18,20,22
	Y= 20	V=28,30,32,34
	Y=30	тV=30,32,34,36

1. Згідно другої формули Ерланга І складеної програми визначаємо ймовірність очікування р(у>0) при заданих значеннях інтенсивності навантаження У і кількості ліній V. Отримані результати зводимо в таблиці У,

2. Згідно даних таблиць 1...3 будуємо сукупність графіків р(γ>0)=Dv(Y)=f(V) для заданих Y(рис1).

3. Визначаємо ефективність використання однієї лінії у = Y/ V для заданих інтенсивності і навантаження Y і р(γ>0). Отримані результати зводимо в таблицю 4. З табл.4 видно, що ефективність навантаження однієї лінії у зменшується майже пропорційно збільшенню кількості ліній. Так, при

збільшенні кількості ліній в 36/32 = 1,12 разів ефективність у зменшується в l,19 разів, при цьому втрати зменшуються в 0,89/0,085 =10,47 разів.

4. Користуючись даними табл.4 або графіками рис.1, визначаємо

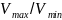=36/20 =1,8 при цьомуD₂₀(20)/ D₃₆(20) - 100/0,085 - 1176,47. З розрахунків видно, що залежність р(у>0)= D_V(Y)= f(V)нелінійна, Так, при збільшенні кількості ліній лише в 1,8 разів втрати вменшуються більше ніж в 1000 разів.

5. Користуючись графіками рис.1, визначаємо залежність ефективності використання однієї лінії від кількості ліній в пучку при заданих втратах р= 5% і р ⁼ 10%. Результати розрахунків зводимо в табл.5.1 і табл.5.2.

З табл.5.1 і табл.5.2 видно, що при постійних втратах і збільшенні інтенсивності навантаження ефективність використання лінії у збільшується, а при постійній інтенсивності навантаження і збільшенні втрату збільшується, що показано на графіках рис.2.

Таблиця 1

V, лінії
ЩшШ

		При Y=		Ерл			Таблиця 1
V, лінії
Dv,%
		При Y=		Ерл			Таблиця 2
V, лінії
Dv,%
		При Y=		Ерл			Таблиця 3
V, лінії
Dv,%

При Y=20 Ерл Таблиця 4

р(γ >0),%
V, лінії
y Ерл.

Таблиця 5.1

При р(γ >0)=5%

y,Ерл,
V, лінії
У.Ерл.

Таблиця 5.2

При р(γ >0)=10%

р,%
V, лінії
y,Ерл,