Практична частина

1.1. Відокремлення коренів. Графічний та аналітичний розв’язок рівняння.

Приклад 1. Відокремити корені рівняння .

Розв’язання. Будуємо графіки функцій і (рисунок 1.1). З графіка видно, що дане рівняння має три корені, причому , , . Оскільки для будь-яких х, а (х) > 2 для і (х) < -2 для х < 0, то інших коренів дане рівняння не має.

Рис. 1.1. Побудова графіків до прикладу 1.1

Приклад 2. Відокремити корені рівняння f(x) = .

Розв’язання.

1. Область визначення X = (-∞; +∞);

2. f '(x)= .Звідси маємо критичні точки .

3. Запишемо інтервали монотонності

;

4. Визначимо знаки функції f(x) на кінцях інтервалів монотонності

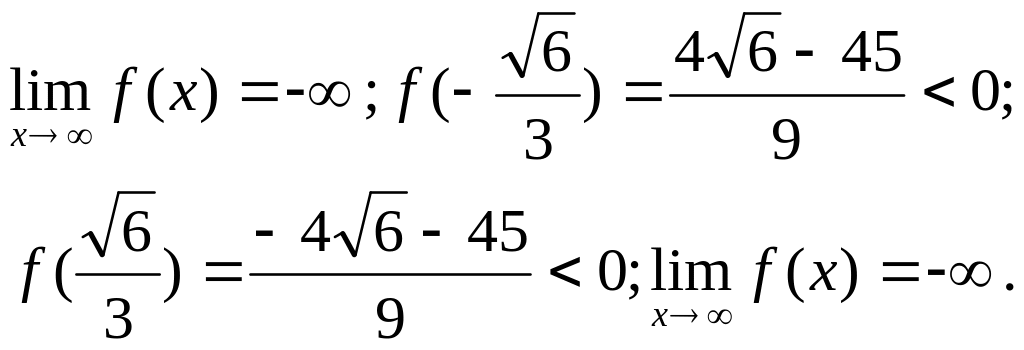
5. Відрізком ізоляції кореня є проміжок .

6. Методом проб звузимо знайдений проміжок ізоляції кореня до одиничної довжини. Оскільки значення близьке до одиниці, то об­числимо f(1) = -6 < 0; f(2) = -1< 0, f(3) = 16 > 0. Отже, корінь даного рівняння належить відрізку [2;3].

1.2. Метод половинного ділення

Алгоритм методу половинного ділення.

1. Ввести, задати значення параметрів а, b та граничної абсолютної похибки  .

2. Обчислити значення функції f (x) в точці а, тобто обчислити f (а).

3. Поділити проміжок [а, b] навпіл, тобто знайти точку x_s

x_s = (a + b)/2.

4. Перевірити умову f (x_s) = 0? Якщо так, то перейти до п.7.

5. Якщо добуток f (а) f (x^*)>0?, то a: = x_s, в протилежному випадку b: = x_s.

6. Якщо |b - a| >  , то перейти до п.3.

7. Надрукувати (вивести) значення x_s.

8. Закінчити виконання програми.

Значення  задається в межах 10 –410 –6.

Приклад 3. Методом половинного ділення знайти розв’язок рівняння з точністю 0,05.

Розв’язання: Побудуємо графік функції (рисунок 1.4.)

Рис. 1.4. Побудова графіку

На основі побудованого графіка функції визначаємо відрізок, який містить корінь: [4.85; 5.2].

Крок 1.

a=4.85; b=5.2;

Крок 2.

Крок 3.

Крок 4

Таким чином, з заданою точністю знайдемо корінь с=5.003.

1.3. Метод хорд

Приклад 4. Знайти додатній корінь рівняння х³ – 2х² +3х –5 = 0.

Визначаємо знаки функцій в різних точках

х	0	1	2	1,5	1,8	1,9
f(x)	–	–	+	–	–	+

Зміна знаку проходить на відрізку [1,8; 1,9].

Обчислюємо значення функцій f(1,8) = – 0,248; f(1,9) = 0,339.

Виходячи з того, що f’(x) = 3х² – 4х + 3 > 0; f’’(x) = 6х – 4 > 0знаходимо наближенні значення за формулою (2)

Отже, це корінь рівняння розташований в інтервалі [1,842; 1,9]. Застосовуємо до цього інтервалу метод хорд

Обчислення значень функцій дають

f(1,843683) = – 2,978·10 ^–4 f(1,8437) < 0

f(1,8438) > 0 f(1,8438) > 0.

Обчислення виконуються доти, доки відмінність між двома послідовно обчисленими значеннями x_{n + 1} i x_n не будуть меншими за ε

.