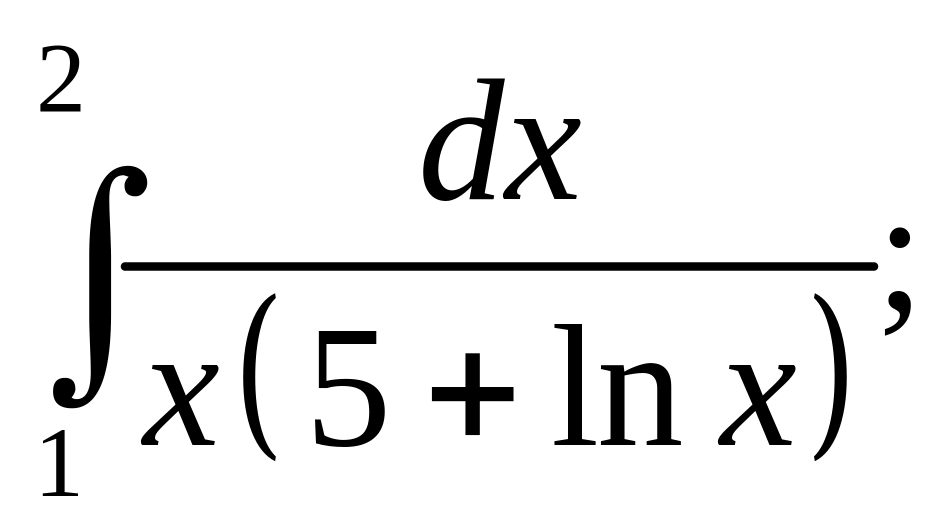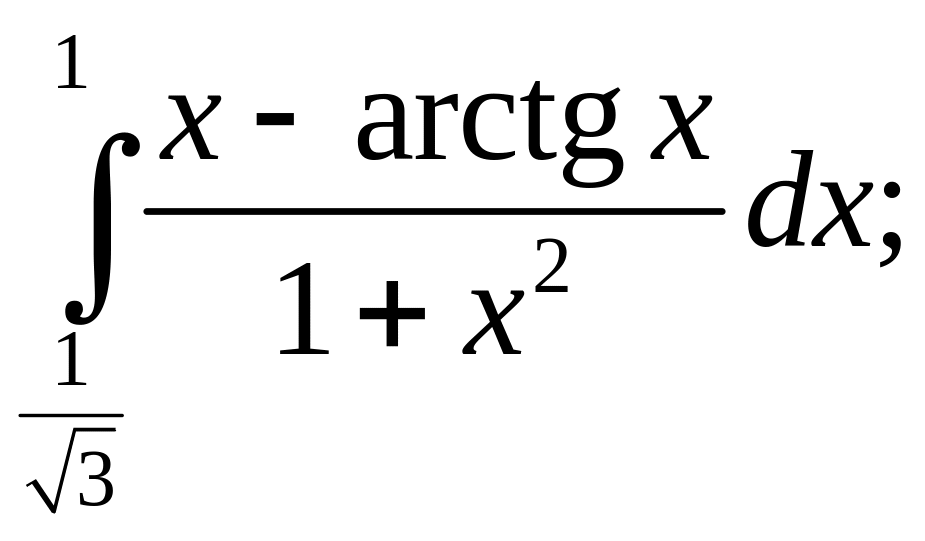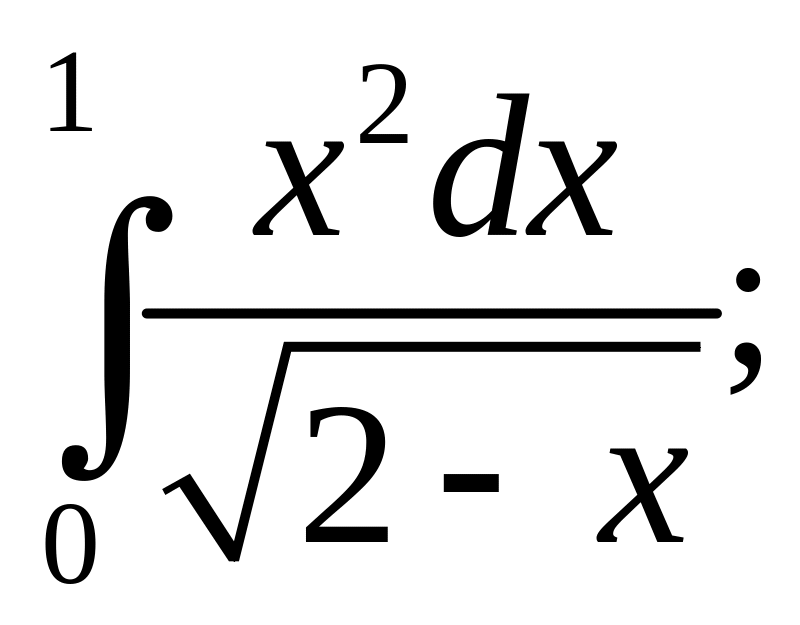1. 2. Метод трапецій
Приклад
2.
Обчислити інтеграл
методом
трапецій за п=10;
Розв’язання:
Для обчислення інтеграла методом трапецій за умови розіб’ємо відрізок інтегрування [0;1] на 10 рівних частин з кроком
.
Складемо таблицю значень підінтегральної функції в точках ділення відрізка:
|
|
|
0 |
0.0 |
0.0000000 |
1 |
0.1 |
0.0009983 |
2 |
0.2 |
0.0079467 |
3 |
0.3 |
0.0265968 |
4 |
0.4 |
0.0623068 |
5 |
0.5 |
0.1198562 |
6 |
0.6 |
0.2032711 |
7 |
0.7 |
0.3156668 |
8 |
0.8 |
0.4991078 |
9 |
0.9 |
0.6344948 |
10 |
1.0 |
0.8414710 |
Обчислення проводимо за формулою
.
Отже
Відповідь: 
0.2290981.
1.3. Метод Сімпсона
Приклад
3. Обчислити інтеграл
методом
Сімпсона за п=8.
Для
обчислення інтеграла методом Сімпсона
за умови 
розіб’ємо
відрізок інтегрування
[1.2;
1.6] на
8 рівних частин з кроком
.
Складемо таблицю значень підінтегральної функції в точках ділення відрізка:
|
|
|
|
|
0 |
1.20 |
1.1211 |
|
|
1 |
1.25 |
|
0.1520 |
|
2 |
1.30 |
|
|
0.1782 |
3 |
1.35 |
|
0.2000 |
|
4 |
1.40 |
|
|
0.2176 |
5 |
1.45 |
|
0.2312 |
|
6 |
1.50 |
|
|
0.2410 |
7 |
1.55 |
|
0.2473 |
|
8 |
1.60 |
0.2503 |
|
|
|
|
0.3713 |
0.8305 |
0.6368 |
Обчислення проведемо за формулою
.
Отже
Відповідь: .0,08278
Індивідуальне завдання №7
1) Обчислити інтеграл за формулою лівих, правих та середній прямокутників.
2) Обчислити інтеграл методом трапецій за n=10;
3) Обчислити інтеграл методом Сімпсона за n=8.
Варіант |
Завдання 1 |
Завдання 2 |
Завдання 3 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
1. Киреев В.И. Численные методы в примерах и задачах: Учеб. пособие / В.И. Киреев, А.В. Пантелеев. – 3-е изд. стер. – М.: Высш. шк., 2008. – 480 с.
2. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие. – 2-е изд., перераб. и доп. – М.: ФИЗМАТЛИТ, 2005. – 304 с.
3. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991. – 272 с.
4. Шуп Т. Решение инженерных задач на ЭВМ: Практическое руководство. Пер. с англ. – М.: Мир, 1982. – 238 с.
5. Бахвалов Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – 5-е изд. – М.: БИНОМ. Лаборатория знаний, 2007. – 636 с.
6. Перегудов Ф.И., Тарасенко Ф.П. Основы системного анализа: Учеб. 3-е изд. – Томск: Изд–во НТЛ, 2001. – 396 с.
7. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. М., 1966. - 664 с.
8. Фалейчик Б.В. Одношаговые методы численного решения задачи Коши: учеб. пособие. – Минск: БГУ, 2010. – 42с.
9. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш. Шк., 2001.