5.4.2. Зведення матричної гри з нульовою сумою до задач лінійного програмування

Матрицю гри великих розмірів графічно зобразити неможливо. Тому таку гру часто зводять до задачі лінійного програмування. Нехай маємо таку матрицю:

Якщо через позначити ймовірність використання стратегії , а через – стратегії , то необхідно знайти такі їх значення, щоб ціна гри сторони А була максимальною.

Цілком зрозуміло, що

.

Тоді знайдемо мішану стратегію , яка забезпечує виграш не менше величини :

у разі відповіді стратегією виграш сторони

у разі відповіді стратегією виграш сторони А

,

де ціна гри також невідома.

Введемо змінні

.

Тоді має місце

(*)

та

.

Оскільки (максимізація виграшу), то

.

Нерівності (*) та цільова функція складають математичну модель задачі лінійного програмування, розв’язок якої дає значення та . За допомогою цих величин знаходять змінні гри та , а також .

Якщо розглядається друга сторона гри В, то треба знайти значення ймовірностей та використання стратегій та . У цьому разі математична модель задачі сторони В є двоїстою задачею до математичної моделі сторони А. Така пара симетрична, тому двоїста задача матиме таку математичну модель:

Зрозуміло, що для сторони А, а для сторони В.

У загальному вигляді математичні моделі двоїстої пари задач лінійного програмування гри з матрицею записуються так:

пряма задача двоїста задача

При цьому

Приклад. Нехай задано таку матрицю:

	0,2	1,0
	0,5	0,25

Треба знайти ймовірність використання стратегій та і величину ціни гри .

Зведемо задачу до математичної моделі задачі лінійного програмування.

Згідно із заданою матрицею

.

Модель лінійної задачі

Наведемо розв’язування задачі різними методами.

1. Графічний метод ЗЛП.

х₂ Область довільних розв’язків задачі

зображено на рис. 5.9.

Точка А – це точка мінімуму. Тому

A розв’язуємо систему рівнянь

х₁

Рис.5.9.

Розв’язок: та .

Тоді

2. Симплексний метод.

Перетворюємо задану модель до стандартного вигляду:

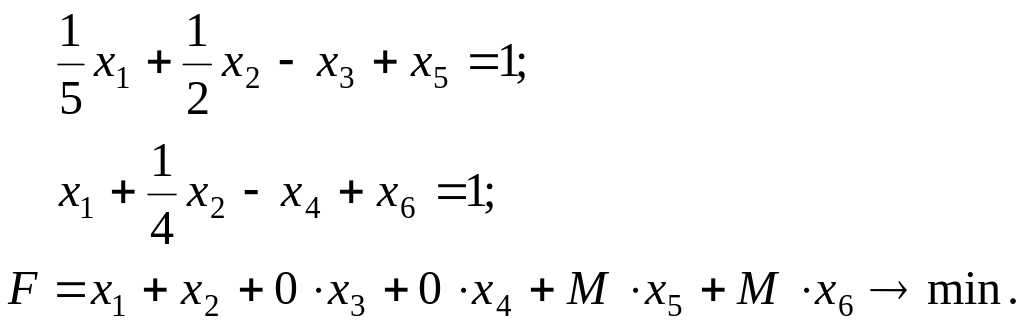
Складаємо три симплекс-таблиці:

					1		1		0		0	М		М
М			1		1/5		1/2		-1		0	1		0
М			1		1		1/4		0		-1	0		1
									-М		-М	0		0
						1		1		0			0		М
М				4/5		0		9/20		-1			1/5		1
М				1		1		1/4		0			-1		0
						0				-М					0

			1	1	0	0
М		4/5	0	1	-20/9	4/9
М		5/9	1	0	5/9	-10/9
			0	0	- 5/9	-2/3

Відповідь:

3. Графічний метод ігрової задачі. Розв’язування показано на рис. 5.10.

Згідно з графіком знаходимо

, , ,

В₁

А₁ А₂

Рис.5.10