4.4. Розв’язування задач

Знаходження оптимального розв’язку та проведення аналізу задачі першого типу виконують за таким алгоритмом.

1. Розв’язування математичної моделі симплекс-методом і знаходження оптимального розв’язку при , але за присутності параметра у симплекс-таблиці.

2. Аналіз величин 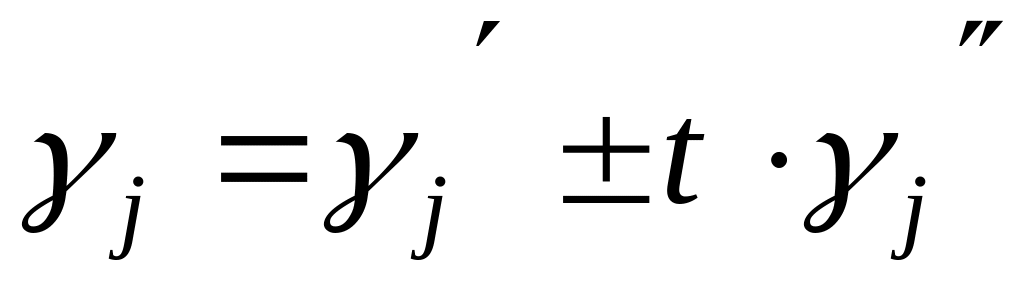. При умови оптимальності мають вигляд , тому знаходять нижню та верхню межі діапазону зміни параметра , в якому оптимальний план не змінюється :

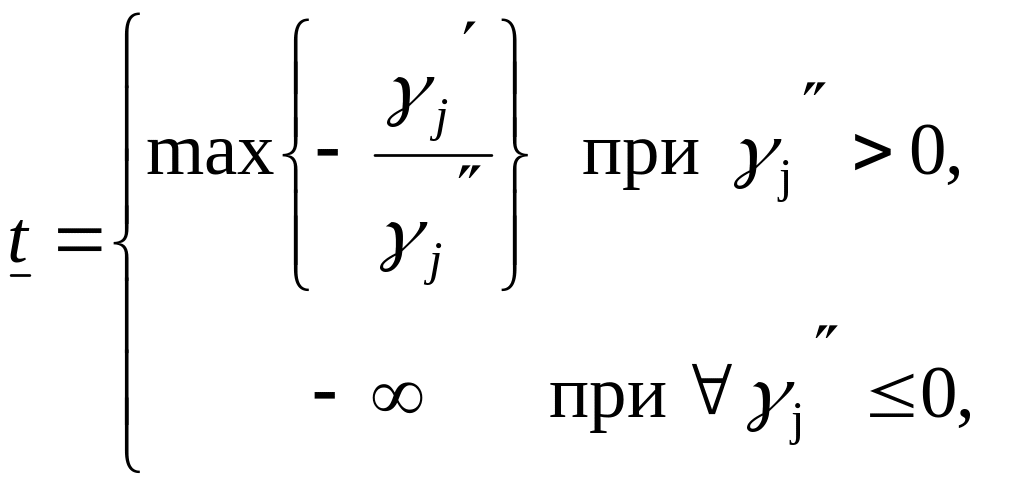
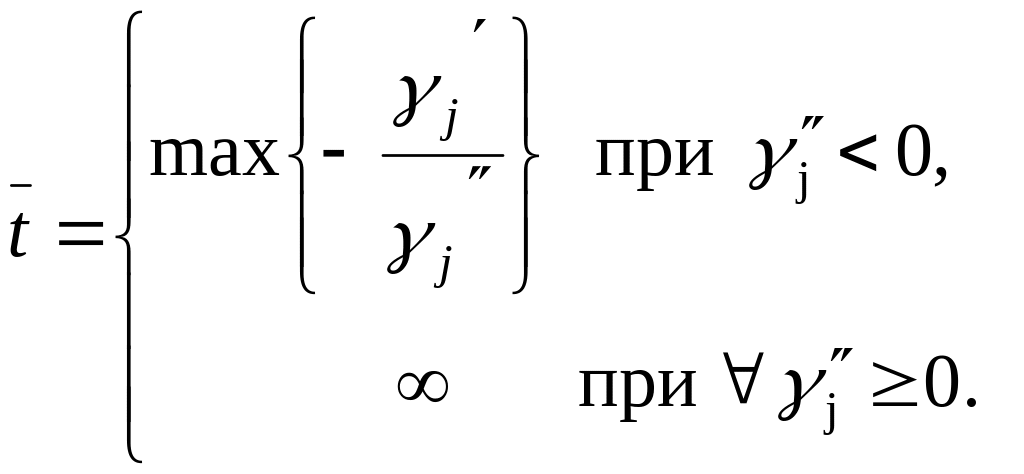
3. Складання діапазону зміни величини :

.

4. Вибір значення , яке не входить до знайденого діапазону та виконання повторного розв’язування задачі за пп. 1-3 для нового значення .

5. Після знаходження всіх діапазонів, в яких є свій оптимальний розв’язок, складається множина діапазонів зі значеннями .

Практично в п.4 використовують симплекс-таблицю, яку знайдено в п.1, та знаходять найближче значення , яке скоріше порушує умови оптимальності, і беруть цю колонку як ключову . Потім переходять до наступної симплекс-таблиці і згідно з п. 2 знаходять новий діапазон параметра .

Якщо неможливо перейти до наступної симплекс-таблиці (відсутні елементи в колонці ), то задача не розв’язується в наступному діапазоні для .

Приклад. Знайти розв’язок математичної моделі

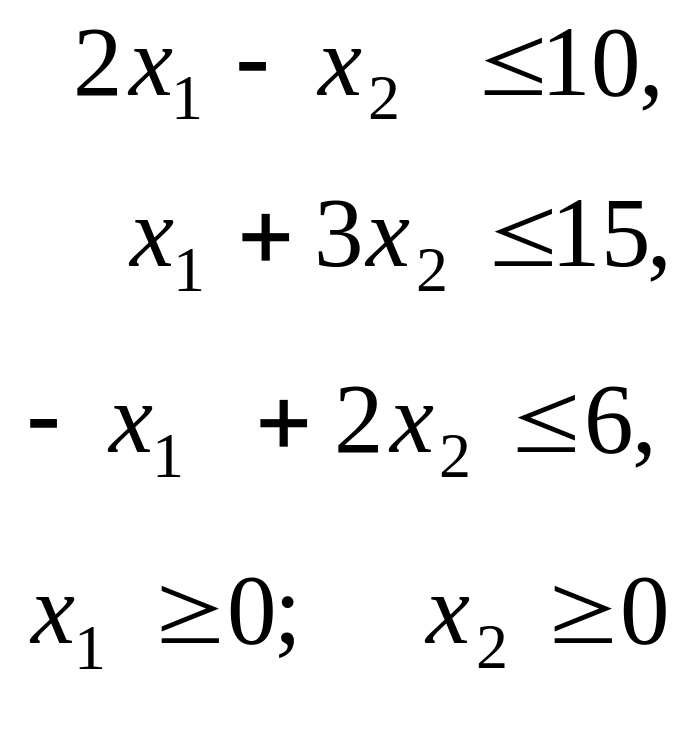
для всіх значень параметра .

Процес розв’язування задачі симплекс-методом наведено у вигляді наступних таблиць:

			3	4-3	0	0	0
0		10	2	-1	1	0	0
0		15	1	3	0	1	0
0		6	-1		0	0	1
			-3	-4+3	0	0	0

			3	4-3	0	0	0
0		13	3/2	0	1	0	1/2
0		13		0	0	1	-3/2
4-3		13	-1/2	1	0	0	1/2
				0	0	0

			3	4-3	0	0	0
0		47/5	0	0	1	-3/5
3		12/5	1	0	0	2/5	-3/5
4-3		21/5	0	1	0	1/5	1/5
			0	0	0

			3	4-3	0	0	0
0		47/7	0	0	5/7	-3/5	1
3		45/7	1	0	3/7	2/5	0
4-3		20/7	0	1	-1/7	1/5	0
			0	0			0

З четвертої таблиці, яка відображує оптимальний розв’язок ( ), знаходимо діапазон для :

та , тобто .

Знайдемо інші діапазони. Якщо , то , тому переходимо до наступної симплекс-таблиці, вибравши головну колонку та генеральний елемент .

Після перетворень дістаємо симплекс-таблицю, яка збігається з третьою симплекс-таблицею. Знайдемо діапазон :

Далі знаходимо розв’язок при . Для цього в четвертій симплекс-таблиці вибираємо , оскільки та і переходимо до наступної симплекс-таблиці:

			3	4-3	0	0	0
0		107/7	0	3	2 /7	0	1
3		25/7	1	-1	4/7	0	0
0		20	0	1	-1	1	0
			0	-11+6t		0	0

Знаходимо діапазон зміни :

Далі аналізуємо . При цьому в п’ятій симплекс-таблиці вибираємо , і складаємо наступну симплекс-таблицю:

			3	4-3	0	0	0
0		54/4	-1/2	-1/2	0	0	1
0		25/4	7/4	-7/4	1	0	0
0		105/4	7/4	-3/4	0	1	0
					0	0	0

Діапазон зміни :

У процесі такого розв’язування знайдено три діапазони зміни в інтервалі . У кожному діапазоні розв’язок не змінюється, а набуває значення залежно від вибраного значення .

Розглянемо процес знаходження оптимального розв’язку та проаналізуємо задачу другого типу. Наведемо схему розв’язування задачі.

1. Розв’язування математичної моделі симплекс-методом і знаходження оптимального розв’язку для = 0.

2. Аналіз усіх величин . Знаходження нижньої та верхньої меж діапазону зміни параметра :

3. Складання діапазону зміни величини

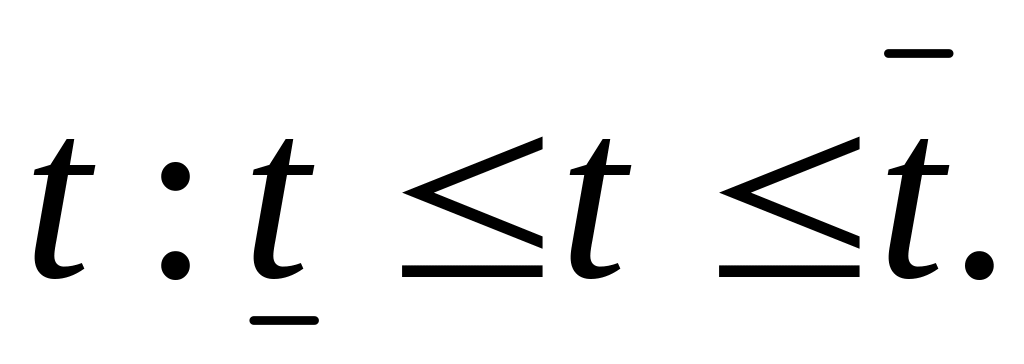
4. Вибір значення , яке не входить до цього діапазону, та повторення розв’язування згідно з пп. 1-3.

5. Формування множини знайдених діапазонів зі значеннями .

Практично в п.4 використовують симплекс-таблицю та знаходять найближчі значення , які порушують умову . Потім згідно з двоїстим симплекс-методом вибирають ключовий рядок .

Якщо ,то задача не має розв’язку для величин цього діапазону.

Розв’язати задачу другого типу можна й так: перетворити математичну модель на двоїсту, тобто перевести модель у задачу першого типу, а потім розв’язати її як задачу з параметром у цільовій функції.

Приклад. Знайти розв’язок такої математичної моделі:

Розв’язування наведемо у вигляді наступних таблиць:

			4	-1	0	0
0			1	6	1	0
0			2	-1	0	1
			-4	1	0	0

			4	-1	0	0
0			0		1	-1/2
4			1	-1/2	0	1/2
			0	-1	0	2

			4	-1	0	0
0			0	1	2/13	-1/13
4			1	0	1/13	6/13
			0	0	2/13	25/13

Знайдемо діапазон зміни :

Потім знайдемо інші діапазони. Якщо , то ключовий рядок = 2, але в цьому рядку відсутні . Тому задача для не має розв’язку. Якщо , то = 1 та оскільки .

Складаємо наступну симплекс-таблицю:

			4	-1	0	0
0		-22	0	-13	-2	1
4			1	6	1	0
			0	25	4	0

Діапазон зміни

Пошук інших діапазонів:

якщо , але відсутні , то задача за цих умов не має розв’язку;

якщо (з попередньої симплекс-таблиці), то = 2 і задача також не має розв’язку.

Унаслідок таких досліджень знайдено два діапазони:

а в діапазонах

задача не має розв’язку.