Висновки

1. Кожна задача лінійного програмування допускає існування двоїстої пари задач: прямої та двоїстої.

2. Розв’язок однієї задачі двоїстої пари з використанням симплекс-таблиці оптимального варіанта або за допомогою теорем двоїстості дає розв’язок двоїстої задачі з цієї пари.

3. Вживання двоїстого симплекс-методу для розв’язування задач лінійного програмування еквівалентне вживанню основного симплекс-методу, причому двоїстий метод спрощує процедуру знаходження оптимального варіанта розв’язку задачі.

4. За допомогою двоїстих оцінок можна проаналізувати рентабельність або збитковість виробництва асортименту продукції.

Контрольні запитання

1. Яку задачу з двоїстої пари доцільно розв’язувати першою і чому?

2. Як знайти математичну модель двоїстої задачі за відомою математичною моделлю прямої задачі?

3. Яким має бути вигляд несиметричної двоїстої пари задач лінійного програмування?

4. Економічна інтерпретація двоїстої пари задач у термінах оптимального розподілу заданих ресурсів.

5. Як знайти оптимальний розв’язок однієї задачі за відомим розв’язком другої задачі з цієї пари?

6. Яка перевага двоїстого симплекс-методу перед основним?

7. У чому полягає різниця між двоїстим та основним симплекс-методами?

8. Як знайти міру дефіцитності початкових ресурсів?

9. Як знайти новий оптимальний розв’язок задачі, якщо початковий ресурс змінився на одиницю?

10. Як визначити види рентабельної та збиткової продукції?

11. Як провести аналіз з метою розширення асортименту вигідної продукції?

РОЗДІЛ 3

ТРАНСПОРТНА ЗАДАЧА

3.1. Властивості та типи транспортних задач

Значний клас задач оптимізації, який належить до задач лінійного програмування, включає так звану розподільну задачу. До неї належать транспортна задача, задача про призначення і розміщення та ін.

Найпоширенішою задачею цього класу є розподільна задача транспортного типу, яка розглядає питання оптимального планування перевезень вантажу, тобто знаходження оптимальних схем вантажопотоків, з’ясування питання оптимальних постачань дефіцитної продукції, закріплення пунктів постачання за споживачами ресурсів та ін.

Зміст та загальний вигляд математичної моделі відомі з п.1.3.2.:

Такі задачі можна розв’язувати симплекс-методом, але через їх специфіку для них розроблені спеціальні методи розв’язання, які простіші у користуванні.

Методи розв’язування задач транспортного типу умовно можна поділити на дві групи:

• методи послідовного поліпшення опорного плану (розподільний метод, метод потенціалів та його модифікації);

• методи послідовного скорочення нев’язок (метод диференціальних рент, угорський метод, метод розв’язувальних елементів);

Найефективнішим і найпростішим у застосуванні є метод потенціалів – спрощений варіант модифікованого симплекс-методу.

Властивості транспортної задачі:

• задача завжди має оптимальний розв’язок;

• якщо значення 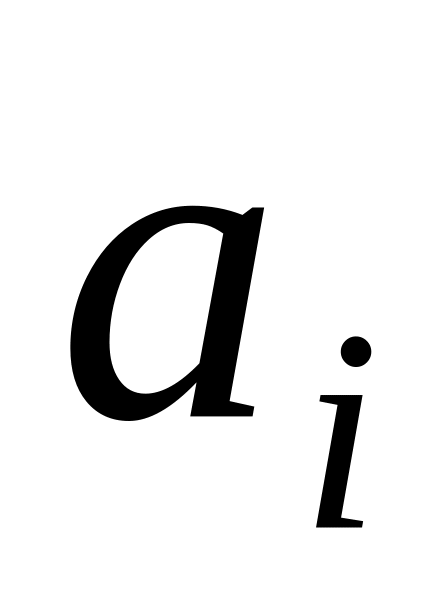та цілі, то розв’язок задачі також цілочисловий, тобто значення цілі;

• обмеження задачі задаються тільки у вигляді строгих рівнянь;

• коефіцієнти змінних в обмеженнях завжди дорівнюють +1;

• кожна змінна зустрічається двічі в обмеженнях задачі;

• кожна змінна має подвійну індексацію.

При розв’язуванні задачі припускається виконання таких умов:

• об’єм постачання ресурсів повинен дорівнювати об’єму споживання цих ресурсів;

• ресурси постачання мають бути повністю вивезені;

• попит споживачів на ці ресурси має бути повністю задоволений;

• витрати на транспортування ресурсів мають бути пропорційними їх обсягам перевезень.

Величини означають, яка кількість ресурсів у знайденому варіанті розв’язку направляється від і-го пункту постачання до -го пункту споживання; вони утворюють матрицю , яку називають планом перевезень. Величини також зображуються у вигляді матриці , яку називають матрицею транспортних витрат, і відображують питомі вартості перевезень вантажу, відстані, час або витрати та ін.

Транспортні задачі поділяють на наступні типи:

• збалансована транспортна задача, коли загальна можливість пунктів постачання дорівнює загальній можливості пунктів споживання, тобто

таку задачу називають закритою;

• не збалансована транспортна задача, коли

у цьому разі обмеження мають вигляд

або

та вказують на зайві ресурси або на підвищений попит їх у споживачів. Таку задачу називають відкритою.

Методи розв’язання транспортної задачі розроблене тільки для закритих задач. Отже, треба всі відкриті задачі звести до закритої. Для цього математичну модель відкритої задачі доповнюють фіктивним пунктом, тобто фіктивним споживачем з попитом

,

або фіктивним пунктом постачання із запасом

.

До цільової функції у цих випадках вводять коефіцієнти , причому ці коефіцієнти для фіктивних пунктів дорівнюють нулю, тобто або .