2.8.1. Міра дефіциту ресурсів

З аналізу сутності другої теореми двоїстості випливає такий висновок: двоїсті оцінки є мірою дефіциту використання ресурсу і: якщо , то і - й початковий ресурс використовується повністю, тобто

.

Такий випадок вказує на дефіцит і-го ресурсу. Якщо , то і-й початковий ресурс використовується не повністю, тобто

.

Якщо відома кінцева симплекс-таблиця, то за індексним рядком можна знайти змінні .

Приклад. Початкові дані наведено у наступній таблиці:

Вид початкового ресурсу	Столи	Шафи	Обсяг ресурсів
Час, людино/годин Деревина, Скло,	18,4 0,6	9,2 1,2 2,0	920 54 40
Прибуток за одиницю, грн.	6	4

Початкова математична модель задачі має вигляд:

За початковими даними складаємо симплекс-таблицю оптимального розв’язку:

			6	4	0	0	0
6		40	1	0	5/92	0	-1/4
0		6	0	0	-3/92	1	-9/20
4		200	0	1	0	0	1/2
			0	0	3/92	0	1/2

Оптимальний розв’язок:

кількість столів шт.,

кількість шаф шт.,

прибуток за місяць грн.

Відповідні змінні:

тобто

Аналіз знайденого розв’язку показує:

• за оптимальним розв’язком повністю використовуються робочий час ( , тобто ) та скло ( , тобто ); ці ресурси є дефіцитом;

• не повністю використовується деревина ( , тобто ); цей ресурс має надлишки, кількість яких

2.8.2. Вплив зміни величини початкових ресурсів на цільову функцію

Згідно з двоїстими оцінками можна проаналізувати зміну цільової функції від зміни обсягів початкових ресурсів.

Для цього використовують третю теорему двоїстості, тобто .

Розглянемо результат розв’язування прикладу:

• збільшення робочого часу на 1 людино-годину дає приріст прибутку на 3/92 грн.( );

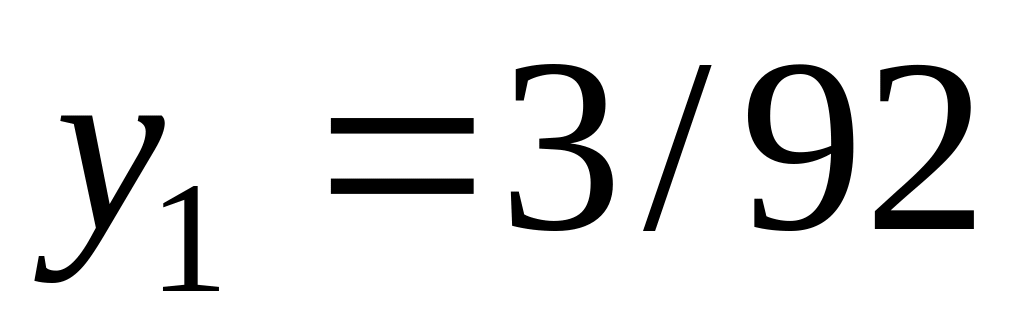• збільшення об’єму скла на 1 дає приріст прибутку на 1,2 грн. ( );

• збільшення об’єму деревини не впливає на збільшення прибутку ( ).

Якщо величина зміни цільової функції при зміні і-го початкового ресурсу на одиницю відома і дорівнює , а величина , то можна поставити питання: як змінюється оптимальний розв’язок, тобто величина . Для цього необов’язково знову розв’язувати задачу симплекс-методом, а треба використати формулу

де – значення базисної змінної, якщо об’єм -го ресурсу змінився на одиницю; – значення базисної змінної знайденого оптимального розв’язку; – значення коефіцієнтів з колонки симплекс-таблиці відповідно до двоїстої оцінки , якщо об’єм ресурсів змінився на одиницю.

Якщо в наведеному прикладі об’єм скла змінити на 1 ( ), то

= 5. Тоді

тобто збільшення об’єму скла зменшує кількість виготовлення столів, але збільшує виготовлення шаф, а надлишок об’єму деревини зменшується з 6 м³ до 5,55 м³.