2.7. Двоїстий симплекс-метод

З математичної моделі двоїстої пари задач випливає, що оцінкою при розв’язуванні прямої задачі є величина C_j_,а для двоїстої задачі . Якщо з цих позицій розглянути симплекс-таблицю, то пряма задача записана обмеженнями по рядках таблиці, двоїста – по колонкам. Оцінки входять до індексного рядка, а оцінки – до базисної колонки правих частин обмежень.

Таким чином, двоїсту пару задач можна зобразити у вигляді однієї симплекс-таблиці. Тільки процес побудови сукупності базисних змінних двоїстої задачі робиться у протилежному напрямку, тобто в першу чергу визначають базисну змінну, яку виводять із базису, а потім змінну, яку треба ввести до базису замість виведеної.

На цій основі розроблено так званий двоїстий симплекс-метод, або метод послідовного уточнення оцінок.

Щоб використовувати двоїстий симплекс-метод, математичну модель задачі треба завжди перетворювати так, щоб у моделі були тільки додаткові змінні, тобто призвести обмеження до вигляду „ ” незважаючи на вимогу .

Тобто, для розв’язання задачі двоїстим симплекс-методом обмеження математичної моделі необхідно звести до типу „ ” незалежно від знаку правої частини та напряму .

Далі наведемо алгоритм двоїстого симплекс-методу.

Вибір у базисній колонці вільних членів елемента, для якого , якщо він існує, якщо , то задача розв’язується основним симплекс-методом.
Вибраний елемент показує на головний рядок .
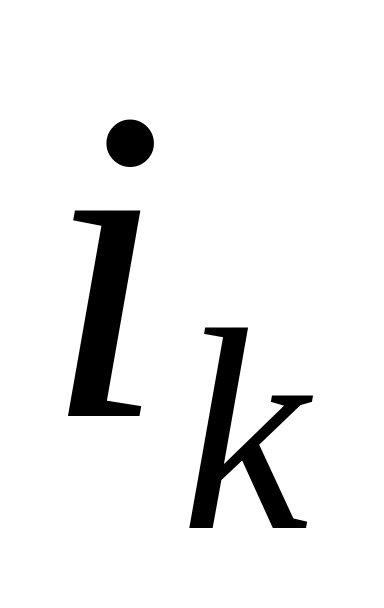Для згідно з головним рядком знаходять невід’ємні симплексні співвідношення, потім з них вибирають максимальне, тобто, якщо , то при 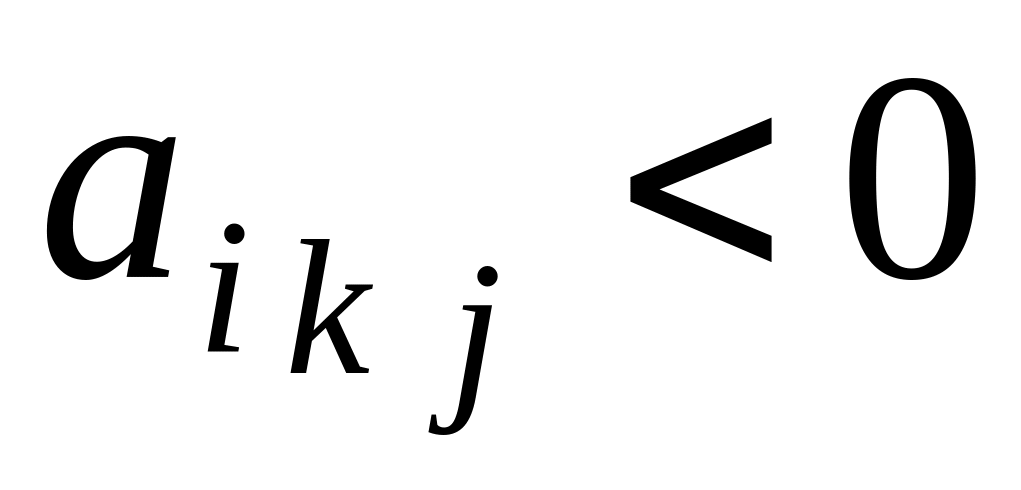, а якщо , то задача не має розв’язку.
Вибране співвідношення зазначає головну колонку .
Перетворення симплекс-таблиці згідно з основним симплекс-методом.
Аналіз знайденого розв’язку на оптимальність:

якщо при або при , то розв’язок задачі вважається оптимальний.

Якщо знайдений розв’язок тільки допустимий, то при виконується перехід до дій п.1; якщо , а величина не виконує умови оптимальності, то виконується перехід до дій п.5.

Зустрічається випадок, коли в початковій симплекс-таблиці , тобто неможливо зробити невід’ємними співвідношення для , оскільки задані коефіцієнти . Тоді треба напрямок цільової функції перетворити на протилежний, тобто

або .

У разі застосування двоїстого симплекс-методу зменшується обсяг обчислень, оскільки не треба виконувати умову у початковій математичній моделі задачі; це означає, що через відсутність штучних змінних розмір задачі зменшується. Тому цей метод доцільно використовувати тоді, коли обмеження мають вигляд „ ”, а також тоді, коли розв’язується задача з наростаючою кількістю додаткових обмежень. Це має місце при розв’язуванні лінійних цілочислових задач методом відтинання, де будується додаткове обмеження. Такий спосіб дає змогу різко зменшити обсяг обчислень у разі появи додаткових обмежень.