3.4.6. Знаходження нового плану розподілу ресурсів

Пошук нового плану розподілу ресурсів зводиться до коригування попереднього плану на величину перерозподілу, причому коригуванню підлягають тільки ті змінні , які ввійшли до циклу перерозподілу. Для визначення величини перерозподілу ресурсів в одержаному плані з усіх значень , тобто з усіх змінних від’ємного напівциклу, вибирають мінімальне

,

що аналогічно виведенню базисної змінної з головного рядка симплекс-таблиці.

У розглянутому прикладі для знайденого циклу величина коригування

.

Потім, ураховуючи знаки змінних, які ввійшли до циклу, та величину , перераховують змінні циклу згідно з формулою

.

При цьому в базис уводиться одна із змінних (у разі виродження плану таких змінних може бути декілька).

Якщо в разі перерахунку у від’ємному напівциклі є більше однієї нульової змінної (тобто має місце виродження плану), то одну (або в разі потреби декілька) з таких змінних залишають як фіктивну базисну.

Процес знаходження нових значень змінних відповідає процесу розрахунку за формулами перетворень елементів симплекс-таблиці у симплексному методі.

Таким чином, новий план відрізняється від попереднього тим, що всі значення , які ввійшли до циклу, корегуються на величину , решта змінних не змінюється.

Оскільки перерозподіляється одиниць ресурсів, а економія від перевезень однієї одиниці вантажу дорівнює , величина нового плану поліпшується на величину , тобто

.

Згідно з побудованим циклом у прикладі та значенням = 20 маємо новий план перевезень, який наведено у наступній таблиці:

	1	2	3
І	30		20	50
ІІ		40		40
	30	40	20

Новий план розподілу знову перевіряють на оптимальність.

1. Складають рівняння потенціалів для всіх ; у прикладі є випадок виродження, тому до системи вводиться ще одне рівняння для фіктивної базисної змінної

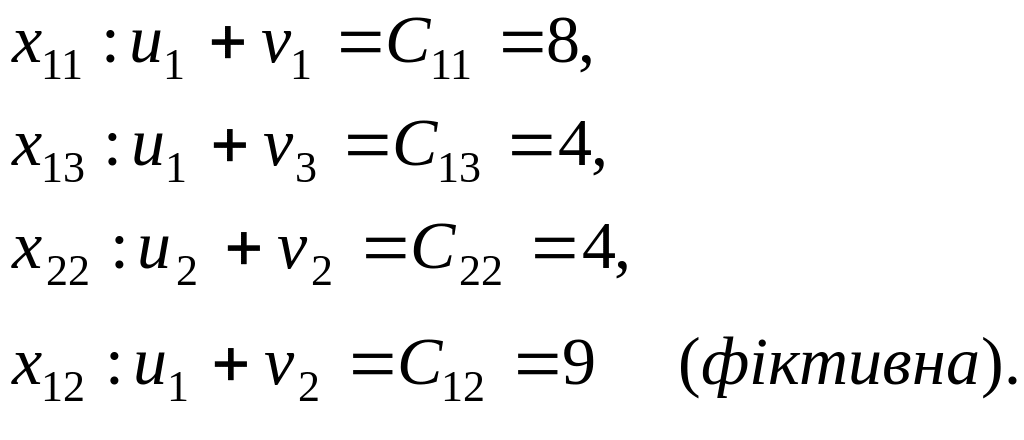
2. З отриманої системи рівнянь знаходять значення потенціалів:

3. Складають рівняння потенціалів для всіх (клітина змінної не входить до цього переліку змінних, оскільки вона фіктивна базисна):

4. Знаходять значення псевдовартостей для згідно з потенціалами та :

5. Перевіряють умови оптимальності:

тобто ці умови оптимальності виконуються для всіх , у зв’язку з цим знайдено оптимальний варіант розв’язку задачі:

решта ,

цільова функція .

Алгоритм розв’язування транспортної задачі зображено на рис. 3.2.

3.5. Альтернативний оптимум

Деякі транспортні задачі мають кілька оптимальних планів, тобто планів, які мають однакові значення . Такі транспортні задачі мають так званий альтернативний оптимум, ознакою якого є наявність хоча б однієї змінної , для якої виконується умова оптимальності

Щоб знайти решту оптимальних планів, треба побудувати цикл, початок якого буде в з Потім розподілити ресурси по цьому циклу, внаслідок чого буде знайдено другий базисний оптимальний план з незмінним значенням .

Наприклад, знайдемо оптимальний розв’язок для наступної транспортної задачі

Математична модель

Побудова початкового базисного розв’язку

Знаходження нового плану:

(для змінних циклу)

Складання системи рівнянь потенціалів

Розв’язування системи рівнянь та знаходження u_i та v_j

Знаходження

Складання рівнянь потенціалів для x_ij = 0

Побудова циклу з початком

в x_ij для

Знаходження псевдо-потенціалів .

Вибір

Оптимальний розв’язок

Рис.3.2

Оптимальний план для цієї задачі наступний:

	1	2	3	4
І		10	20		30
ІІ				30	30
ІІІ	30	10			40
ІV		5			5
	30	25	20	30

Цільова функція цього плану

З аналізу на оптимальність випливає, що для маємо

Тому можна знайти другий базисний оптимальний план згідно з циклом за допомогою величин перерозподілу

У нового плану також

	1	2	3	4
І		10		20	30
ІІ			20	10	30
ІІІ	30	10			40
ІV		5			5
	30	25	20	30

Для цього плану:

1. 

2. 

3. 

Для знаходження інших оптимальних планів можна використати формулу відрізка

,

де – значення з першого та другого базисного оптимального плану.

Для :

Можна також використати формулу

для змінних, які ввійшли до циклу. Наприклад, для та циклу маємо

Існування множини оптимальних розв’язків дає можливість при розв’язуванні транспортної задачі використовувати також інші критерії. Тому в цьому разі можна застосовувати метод послідовних критеріїв.