1.5.4. Початковий базисний розв’язок

Розв’язування задачі симплекс-методом полягає в знаходженні першого базисного розв’язку (першого опорного плану) та послідовному його поліпшенні для одержання оптимального варіанта.

При використанні симплекс-методу найбільш зручною формою є таблична. Ця форма потребує, щоб цільова функція та обмеження мали вигляд

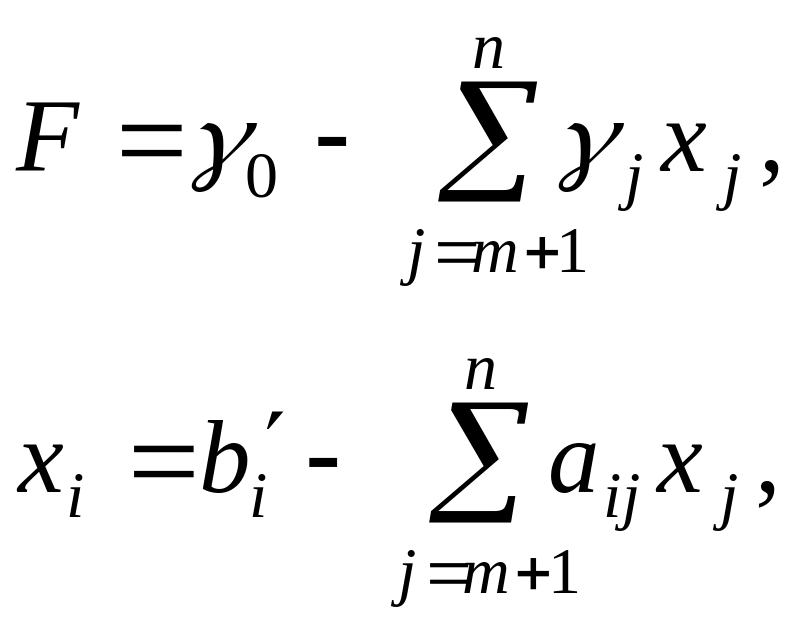
де базисними змінними вибрано перші т змінних математичної моделі задачі.

Перша симплекс-таблиця будується з математичної моделі розширеної форми.

Структура симплекс-таблиці наступна:

– рядок переліку змінних та ;

– рядок коефіцієнтів при відповідних змінних з цільової функції та ;

– основна частина таблиці у вигляді матриці коефіцієнтів при змінних з обмежень, ця матриця містить також невід’ємну одиничну матрицю;

– три базисні колонки для запису вільних членів , базисних змінних та їх коефіцієнтів з цільової функції;

– індексний рядок з коефіцієнтами та .

Початкову симплекс-таблицю заповнюють у такій послідовності.

Два верхніх рядки таблиці зображують цільову функцію: другий рядок зверху заповнюють змінними моделі, включаючи основні, додаткові та штучні, а перший рядок – коефіцієнтами при змінних з цільової функції.

Оскільки всі додаткові та штучні змінні з коефіцієнтами +1 утворюють одиничний базис, то

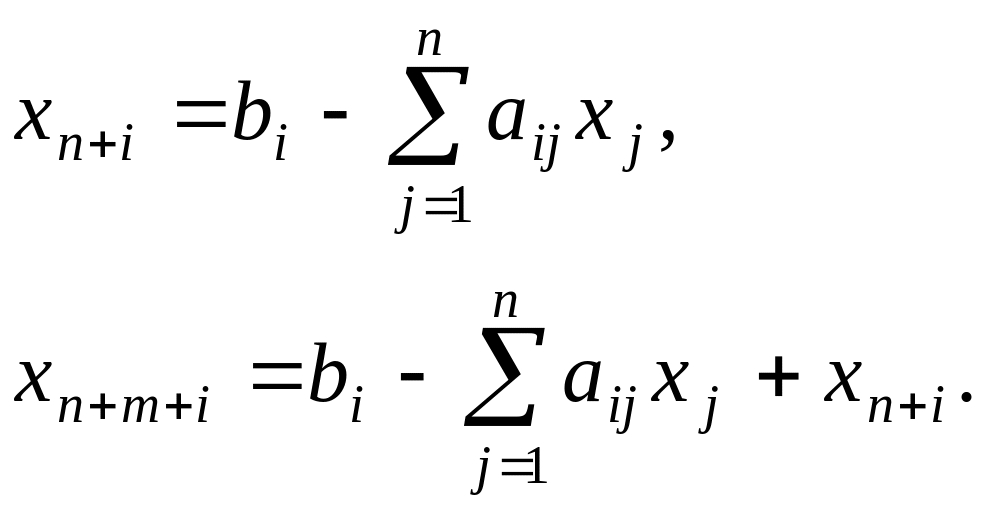
Такі змінні позначають та записують у середню базисну колонку, а коефіцієнти при цих змінних з цільової функції у ліву базисну колонку. До правої базисної колонки записують праві частини з обмежень моделі.

Кожний рядок таблиці зображує одне обмеження моделі за допомогою коефіцієнтів при відповідних змінних. Взагалі такий запис обмежень моделі утворює матрицю .

Нижній рядок таблиці, який називають індексним, призначений для аналізу знайденого варіанта розв’язку на оптимальність. Елементами цього рядка є коефіцієнти , які розраховують за формулою

Іноді індексний рядок зображують двома рядками, в одному з яких записують значення

а в іншому – коефіцієнти (- ); таким чином, індексний рядок набирає огляду .

Загальний вигляд основної частини симплекс-таблиці наступний:

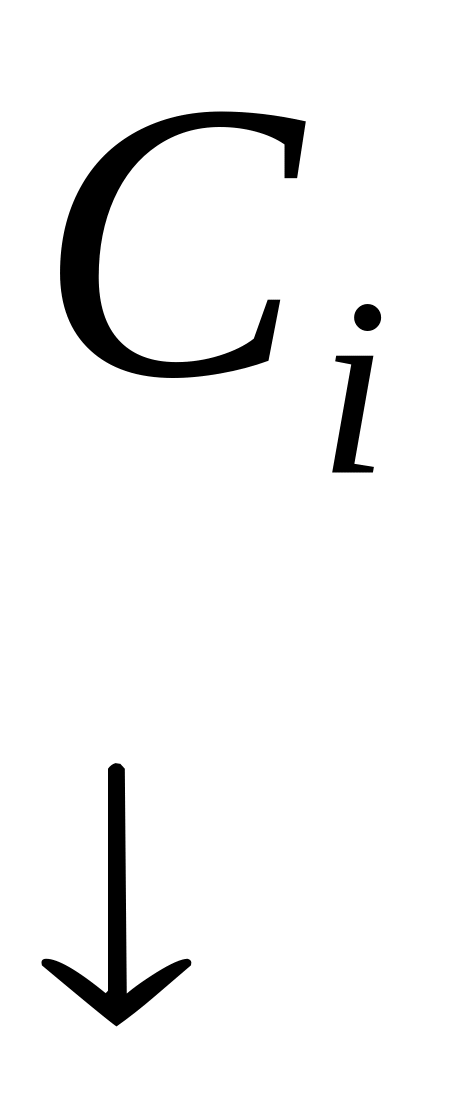
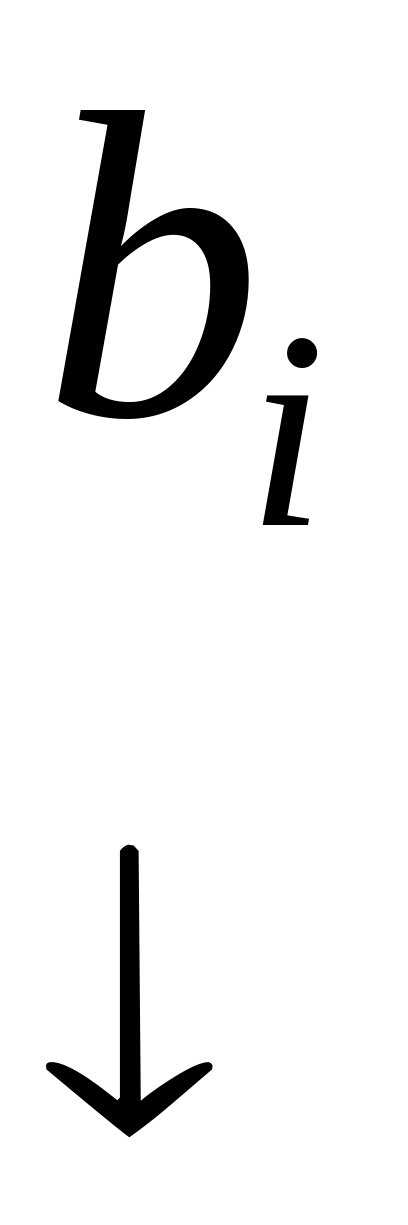
			Коефіцієнти
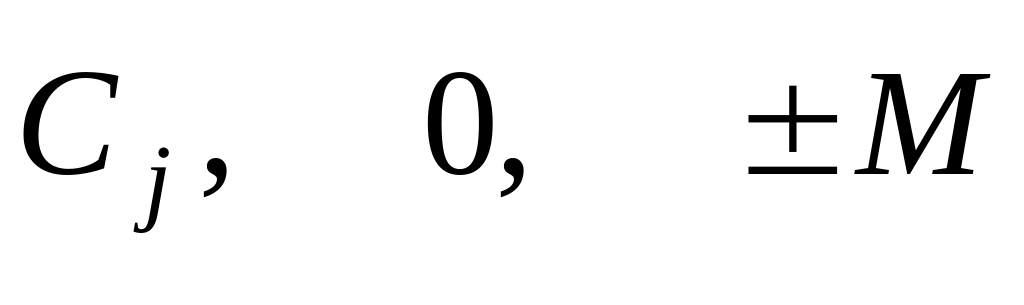
			Змінні
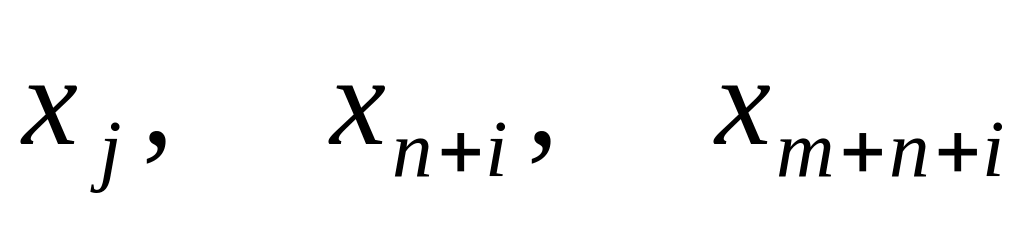
			Коефіцієнти при змінних з обмежень тобто
			Коефіцієнти

Базис

Індексний рядок

Для кожного допустимого розв’язку задачі всі змінні, які записано до базису, дорівнюють

а всі вільні змінні, тобто змінні, які не ввійшли до базису, .

1.5.5. Алгоритм перетворення

Процес поліпшення варіанта розв’язку задачі полягає в перетворенні збудованої симплекс-таблиці в наступну симплекс-таблицю в такій послідовності.

1. Якщо добутий варіант розв’язку не виконує умови оптимальності, то в індексному рядку знаходять елемент , який найбільше порушує ці умови. Тобто при вибирають найбільш невід’ємний елемент , при – найбільш від’ємний елемент . Такий вибір елементів дає можливість змінити значення на максимальну величину при побудові наступної симплекс-таблиці.

2. Вибраний елемент індексного рядка означає головну колонку симплекс-таблиці. Ця колонка повинна мати хоча б один невід’ємний елемент . Якщо в ній такого елемента немає, то слід узяти наступний за відповідною ознакою ( , або ) елемент індексного рядка. Випадок, коли 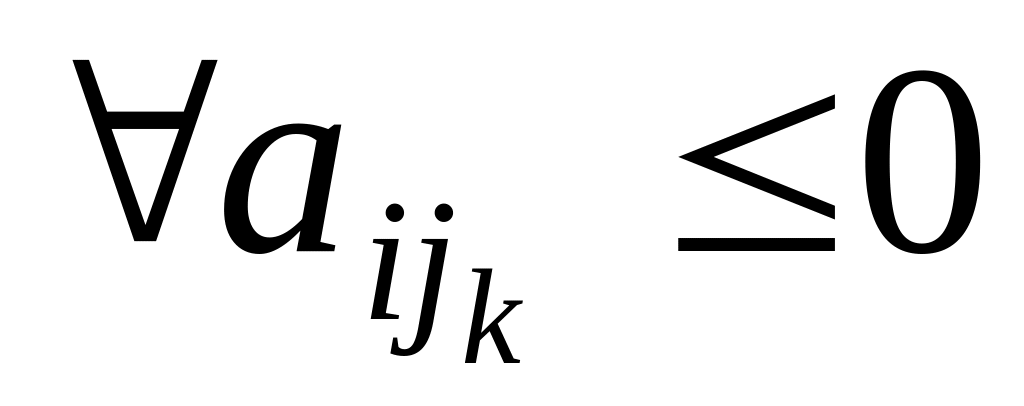для вибраних колонок, означає, що розв’язок задачі необмежений, тобто

3. Кожний вільний член ділять на відповідний елемент головної колонки і знаходять по кожному рядку симплексні співвідношення. Ще раз підкреслимо: ділять тільки на елементи

4. Вибирають мінімальне значення симплексного співвідношення

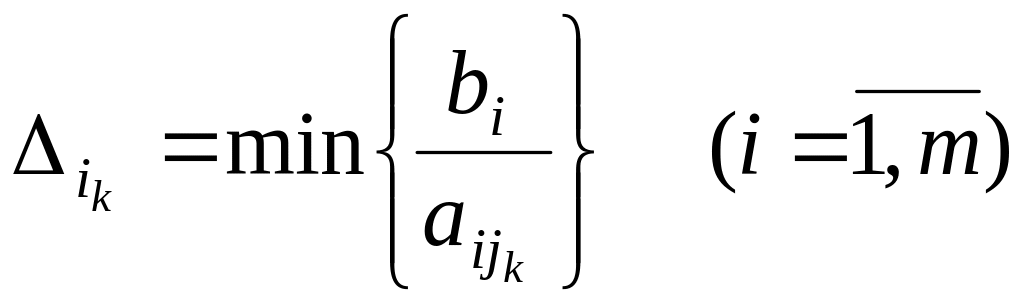
для того, щоб не порушити умови . Якщо є кілька однакових мінімальних співвідношень, то доцільно вибрати з них таке, яке передбачає виведення з базису штучної змінної, або в якого значення максимальне.

5. Мінімальне співвідношення відповідає головному рядку симплекс-таблиці.

6. На перетині головного рядка та головної колонки находиться генеральний, або, як його часто називають, розв’язувальний елемент Чому він має індекси ? .

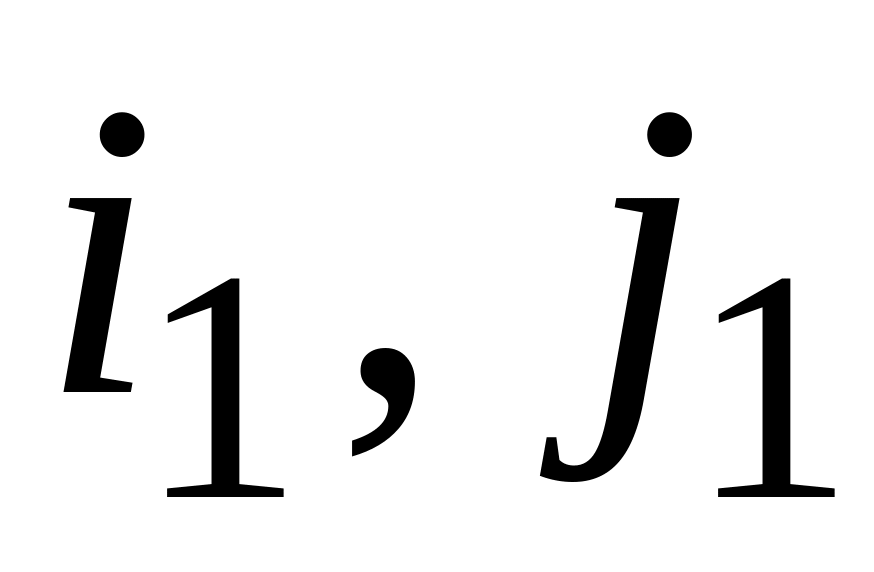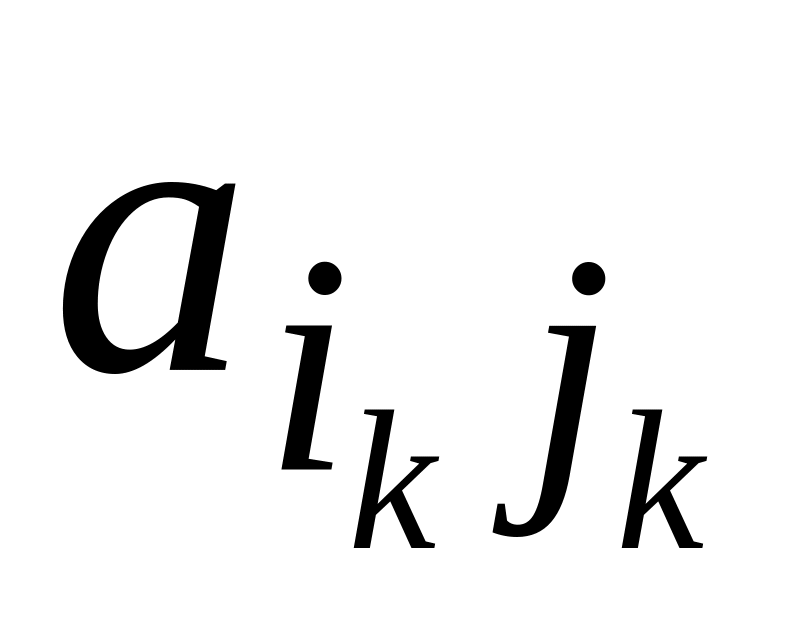7. Перетворюють елементи симплекс-таблиці за формулами

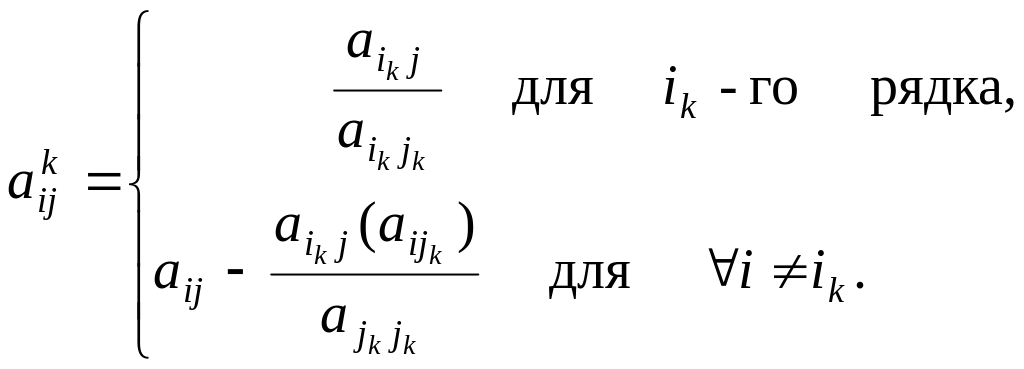
8. Складають нову сукупність базисних змінних, для чого змінну 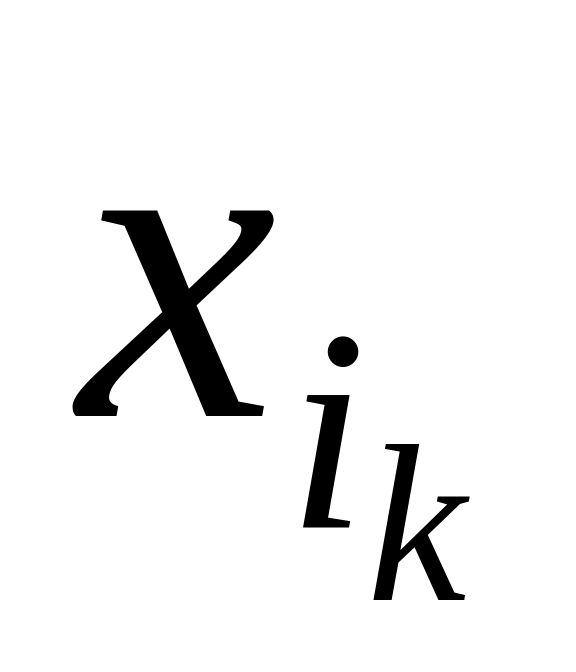заміняють на , інші базисні змінні не змінюють.

9. Аналізують на оптимальність новий варіант розв’язку за одержаною симплекс-таблицею.

10. Якщо умови оптимальності виконуються, то переходять до виконання дій п.11, у протилежному разі – до дій п.1.

11. Знаходять числові значення оптимального варіанта:

• базисні змінні дорівнюють відповідним значенням 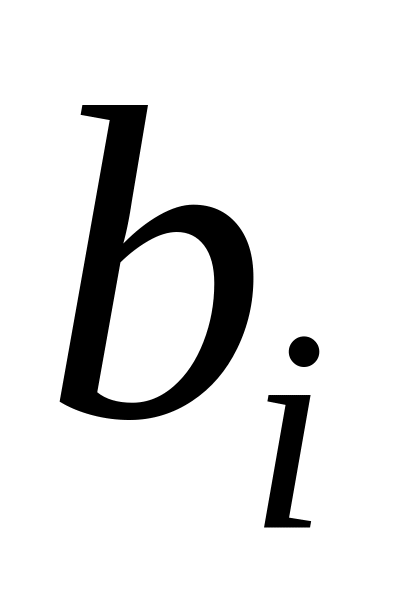, небазисні (вільні) змінні – нулю;

• значення цільової функції 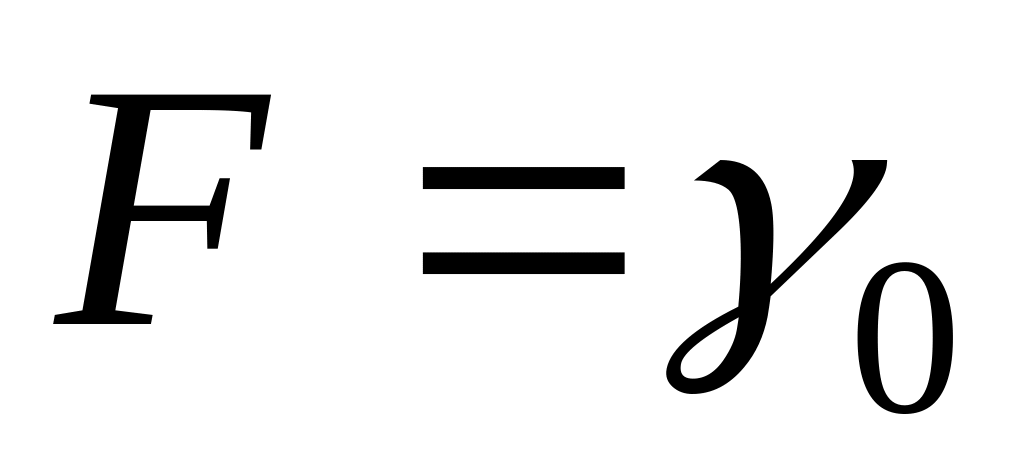, якщо обчислювалось у процесі перетворення симплекс-таблиць, або після підстановки до її виразу знайдених значень змінних.

Алгоритм перетворення у загальному вигляді наведено на рис.1.12.

Кількість переходів від однієї симплекс-таблиці до іншої (так звана симплекс-ітерація) з метою знаходження оптимального варіанта (якщо він існує) залежить не від кількості змінних, а від кількості обмежень в діапазоні

Математична модель

Зведення моделі до

стандартного вигляду

Складання першої

симплекс-таблиці

План

оптимальний

Так

Вибір згідно з

умовами оптимальності

Ні

Вибір колонки

Вибір рядка згідно з

Вибір головного елемента

Перетворення елементів

симплекс-таблиці

Складання нової сукупності базисних змінних

Рис.1.12 Ліва стрілка вниз

1,5т...3,0т; кількість обчислювальних операцій одного симплекс-перетворення дорівнює приблизно 2тп.

У процесі знаходження оптимального варіанта треба мати на увазі:

• якщо в головній колонці немає невід’ємних елементів, то це означає, що значення необмежене в напрямку пошуку;

• якщо в знайденому оптимальному варіанті до сукупності базисних змінних входить штучна змінна, то це означає, що задача не має розв’язку оскільки обмеження моделі несумісні;

• якщо в оптимальному варіанті будь-яка вільна змінна має в індексному рядку оцінку , то задача має множину оптимальних розв’язків; цілком зрозуміло, що коли всі вільні змінні 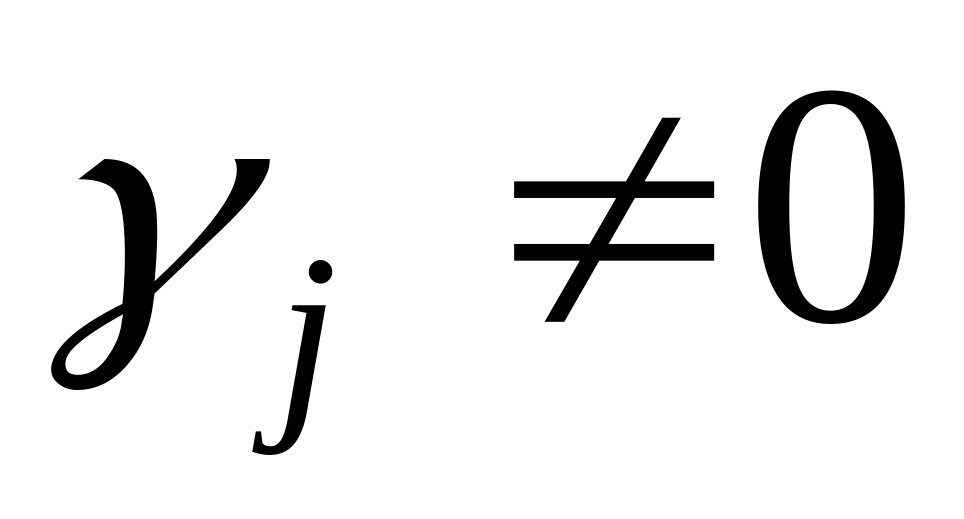, то це є ознакою тільки одного оптимального розв’язку;

• величини в індексному рядку кінцевої симплекс-таблиці вказують на діапазон 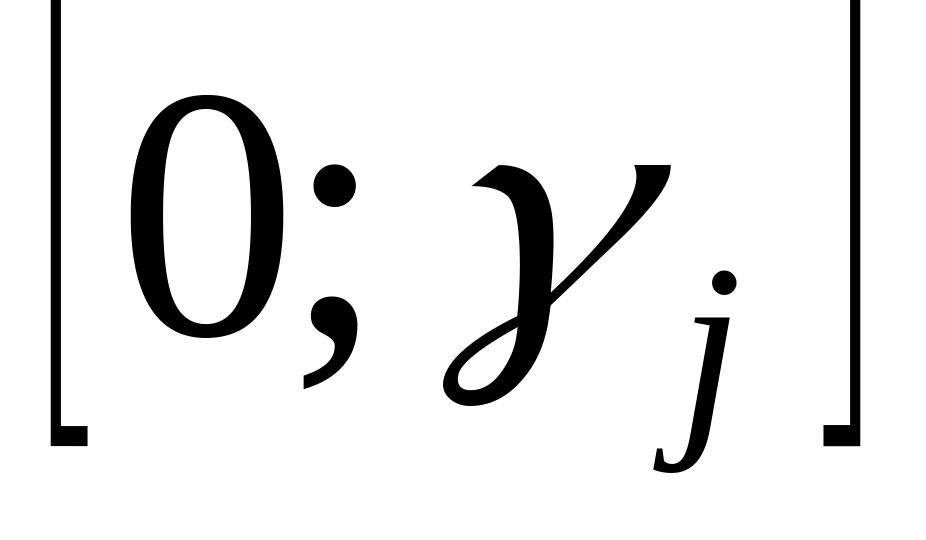, в якому можна змінювати відповідні коефіцієнти цільової функції без зміни оптимального розв’язку; при цьому значення можна знайти з виразу

.

Розглянемо приклад знаходження оптимального розв’язку симплекс-методом.

Нехай задано таку математичну модель:

• цільова функція

• обмеження

за умови .

Наведену модель перетворюємо до розширеної форми:

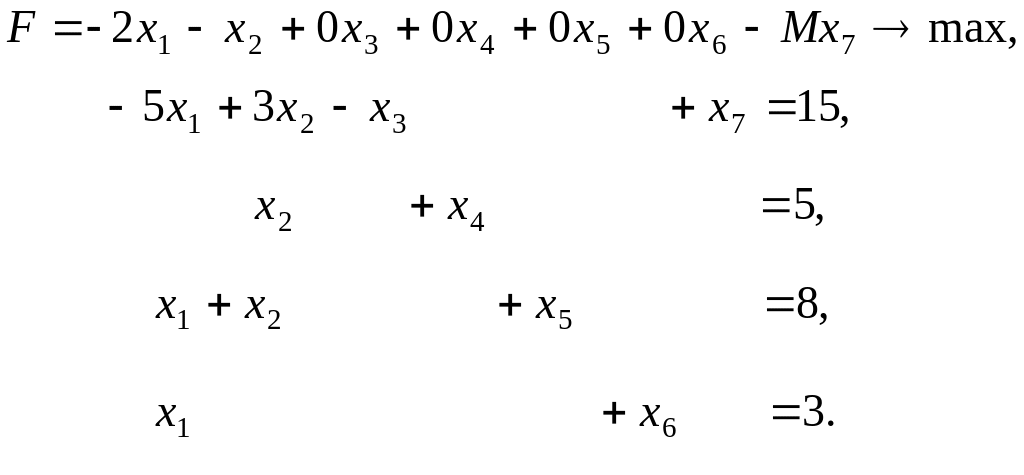
Спочатку складаємо першу симплекс-таблицю:

			-2	-1	0	0	0	0	-М
-М		15	-5	3	-1	0	0	0	1
0		5	0	1	0	1	0	0	0
0		8	1	1	0	0	1	0	0
0		3	1	0	0	0	0	1	0
			5М +2	-3М + 1	М	0	0	0	0

Розв’язок знайдено тільки допустимий, тому знаходимо та . Потім складаємо другу симплекс-таблицю згідно з алгоритмом перетворення:

			-2	-1	0	0	0	0	-М
-1		5	-5/3	1	-1/3	0	0	0	1/3
0		0	5/3	0	1/3	1	0	0	-1/3
0		3	8/3	0	1/3	0	1	0	-1/3
0		3	1	0	0	0	0	1	0
			11/3	0	1/3	0	0	0	М -1/3

Знайдений розв’язок є оптимальним:

• базисні змінні

• вільні змінні

Цільова функція має значення