1.3.2. Транспортна задача

Транспортні задачі часто зустрічаються на практиці і характерні для класу розподільних задач, наприклад, оптимальне розміщення вантажу, складання оптимальних маршрутів, доставка продуктів, які швидко псуються, та ін. Іноді транспортну задачу називають Т-задачею.

Змістова постановка транспортної задачі така.

Є пунктів постачання та пунктів споживання декотрого однорідного продукту. Відомі обсяги можливого постачання продукту від кожного пункту постачання та обсяги попиту кожного пункту споживання, а також витрати , які пов’язані з перевезенням одиниці продукту від і-го пункту постачання до j-го пункту споживання.

Необхідно знайти такий план перевезення продукту, щоб загальна вартість перевезення цього продукту була мінімальною.

Позначимо через змінні кількість вантажу, яку належить перевезти з і-го пункту постачання до j-го пункту споживання. Тоді загальна кількість вантажу, що йде з і-го пункту постачання до всіх пунктів споживання має вигляд

а кількість вантажу, що приймається j-м пунктом споживання від усіх пунктів постачання

Мета задачі має вигляд

за умови .

Приклад. Існує три пункти постачання з відповідними запасами ресурсів (вантажу)

та два споживача ресурсів з відповідним попитом

Вартість перевезень одиниці вантажу задано у вигляді матриці

^.

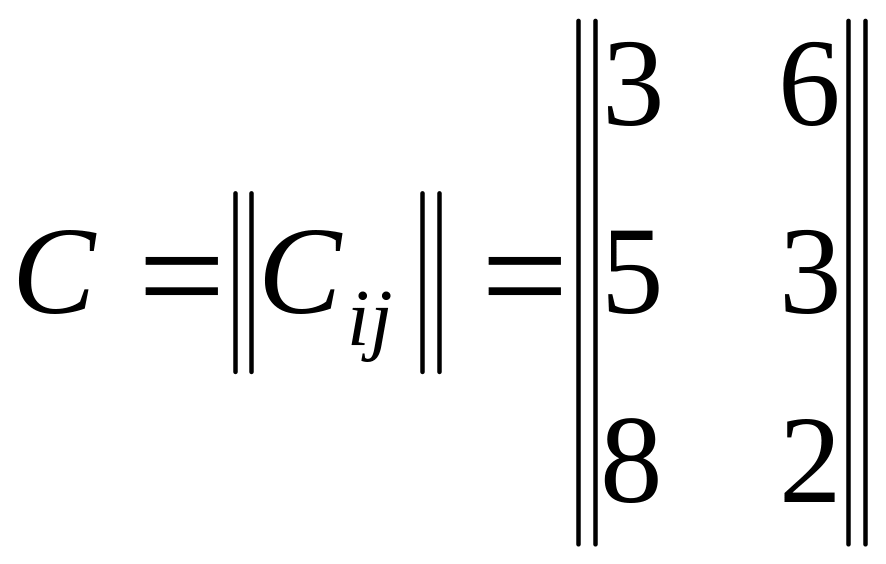Скласти математичну модель задачі, яка передбачає мінімальні транспортні витрати перевезень ресурсів.

Математична модель має такий вигляд:

• цільова функція

• обмеження за пунктами постачання

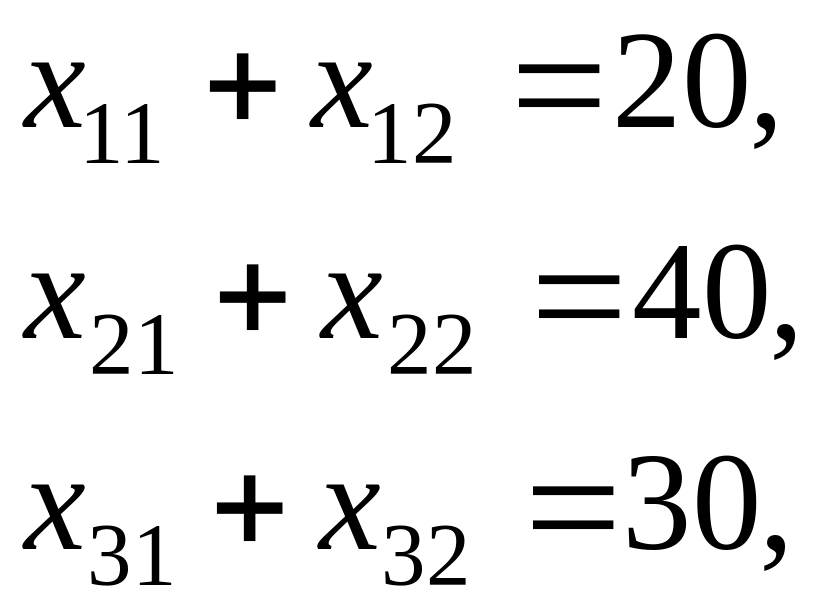
• обмеження за пунктами споживання

Розглянуті математичні моделі типових задач лінійного програмування не вичерпують усіх задач, що зустрічаються на практиці. Але за допомогою певних перетворень всі вони зводяться до загальної задачі математичного програмування.

1.4. Графічний метод

Графічний метод розв’язування задач лінійного програмування ґрунтується на геометричному зображенні математичної моделі задачі в системі координат. Але його використання обмежено зростанням кількості змінних у задачі,. Як на мене, краще не писати „зобразити задачу”. Тому в основному цей метод використовується для задач, які мають дві-три змінні, або якщо різниця між кількістю змінних та кількістю обмежень задовольняє умові (т – п) < 2. У цьому випадку математичну модель задачі потрібно перетворити так, щоб вона мала вигляд двовимірної.

Основна перевага графічного методу полягає в простому зображенні та наочності ходу розв’язування.

Графічний метод реалізується в два етапи:

– побудова ОДР;

– знаходження оптимального розв’язку.

Зауважимо, що в процесі побудови ОДР можливі такі випадки:

– порожня область (рис.1.8, а); при цьому обмеження в математичній моделі несумісні і згідно з цим задача не має розв’язку;

– опуклий многогранник (рис. 1.8, б); при цьому обмеження сумісні та зображують область, до якої входять допустимі розв’язки;

– необмежена область з одного боку (рис. 1.8, в-г); при цьому існує мінімум або максимум, або взагалі не існує розв’язку.

Наведемо алгоритм розв’язування задачі лінійного програмування графічним методом.

1. Згідно з обмеженнями математичної моделі задачі будують ОДР. Для цього всі нерівності обмежень подають рівняннями безпосередньою заміною знаків „ ” та „ ” знаком „=”. Кожне знайдене рівняння зображують на площині прямою, яку будують за двома довільними точками. Кожна така пряма поділяє площину на дві півплощини – допустиму та недопустиму, а сама пряма є межею цих півплощин.

Щоб знайти допустиму півплощину, треба взяти дві довільні точки в кожній півплощині та їх координати підставити до заданого обмеження: точка, яка порушує знак обмеження, є точкою недопустимої півплощини, а точка, яка не порушує знака, знаходиться в допустимій півплощині (для такого аналізу доцільно використовувати нульову точку, тобто початок координат, якщо пряма не проходить через початок координат).

Після побудови всіх допустимих півплощин знаходять ОДР як перетин цих півплощин з урахуванням умови .

а) б)

в) г)

Рис.1.8

2. Будують пряму цільової функцію у такій послідовності:

• за двома точками (точкою початку координат та точкою, координати якої є коефіцієнти при відповідних змінних з цільової функції) будують градієнт функції, який показує напрямок максимальної зміни значення цільової функції ;

• перпендикулярно до градієнта будують пряму цільової функції, наприклад, через початок координат, де = 0).

3. Знаходять місце розміщення оптимальних точок у допустимому просторі. Для цього пряму цільової функції зсовують паралельно собі у напрямку градієнта: найближча точка дотику ОДР відповідає точці мінімуму, а найвіддалена – точці максимуму.

4. Знаходять координати точок дотику ОДР. Для цього розв’язують систему рівнянь прямих, які утворюють ці точки. Наслідок розв’язування таких систем рівнянь дає оптимальні значення змінних, які потім підставляють у вираз цільової функції та знаходять значення чи .

Іноді лінії рівня цільової функції розташовується паралельно одній з границь ОДР. У цьому разі задача має множину оптимальних розв’язків з постійним значенням . Такі задачі називають задачами з альтернативним оптимумом.

Послідовність розв’язування задачі графічним методом зображено на рис.1.9.

Приклад. Знайти оптимальний розв’язок для такої математичної моделі:

– цільова функція

;

– обмеження

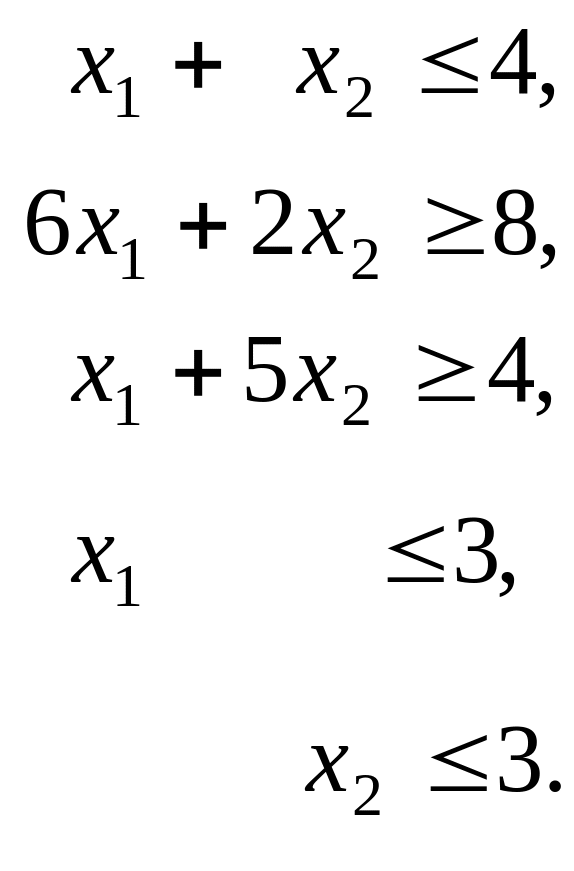
Математична модель

і=1

Перетворенння і-го

обмеження у пряму

Побудова і-ої прямої

Знаходження допустимого

півпростору

і=і + 1

Знаходження ОДР

=

Побудова градієнта

Вибір найближчої точки дотику

Вибір найвіддале-ної точки дотику

min max

Знаходження координат

точки екстремуму

Знаходження значення

Оптимальний розв’язок

Рис.1.9

за умов

Згідно з обмеженнями задачі будуємо ОДР (рис. 1.10).

Спочатку будуємо градієнт цільової функції F через нульову точку та точку А з координатами ; потім – пряму цільової функції F перпендикулярно до побудованого вектора. Пряму F зсовуємо в напрямку вектора до найближчої точки дотику ОДР – точки В, яка утворюється прямими та . Розв’язуючи систему цих рівнянь, знаходимо та , а значення цільової функції =4.

qrad F

А

В

F=0

Рис.1.10