1.2. Загальна характеристика задачі лінійного програмування

Постановку задачі лінійного програмування характеризують такі особливості:

• наявність умов, за допомогою яких обмежують пошук оптимальних розв’язків задачі, ці обмеження повинні бути лінійними та мати вигляд рівняння чи нерівності ;

• існування області допустимих розв’язків (ОДР), тобто задача повинна бути варіаційною;

• критерій оптимальності, який надається у вигляді лінійної залежності

• адитивність обмежень і цільової функції

та

• пропорційний вигляд залежності витрат кількості ресурсів використання;

• невід’ємність змінних 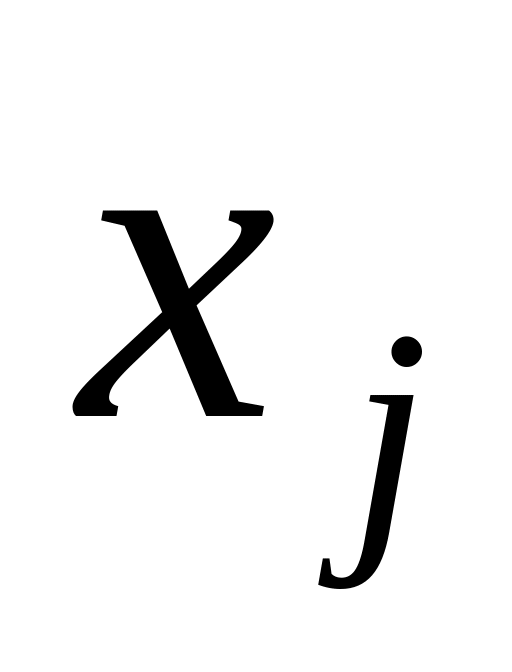, тобто , де .

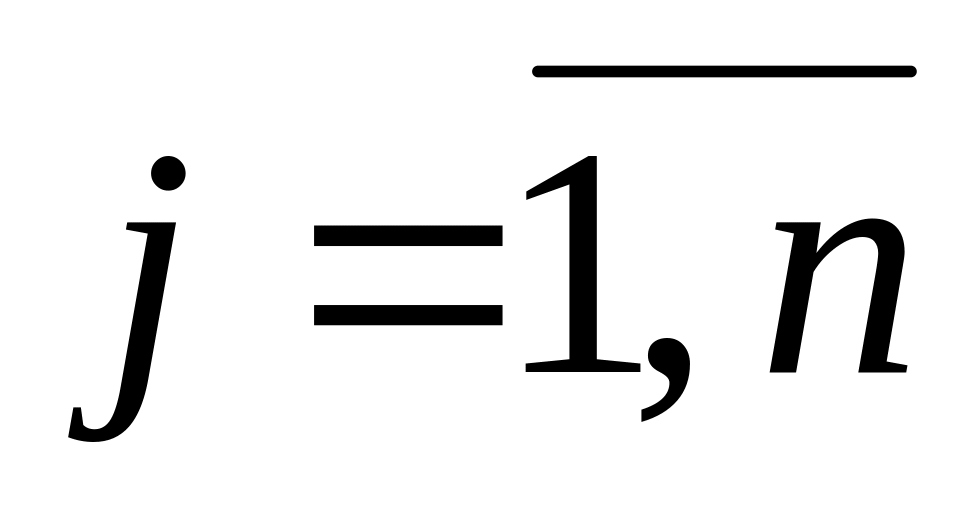Задача лінійного програмування має такі властивості:

1. Множина допустимих розв’язків зображується у вигляді опуклої фігури.

У задачах лінійного програмування область допустимих розв’язків завжди опукла, оскільки утворюється перетином опуклих областей півпросторів (у двовимірному просторі – півплощинами) обмежень задачі. Опуклий многогранник цієї області має скінчену кількість кутових точок.

2. Видалена фраза не зрозуміла. Може взагалі цей пункт прибрати? Гіперплощини з різними значеннями цільової функції взаємно паралельні, у випадку двовимірного простору – це паралельні прямі.

3. Локальна точка екстремуму є одночасно глобальною (абсолютною).

4. Оптимальний розв’язок задачі знаходиться в одній з кутових точок многогранника області допустимих розв’язків. Тобто, точка оптимального розв’язку не може бути всередині області допустимих розв’язків оскільки для внутрішніх точок

.

Таким чином, гіперплощина, яка відображує оптимальне значення цільової функції, повинна тільки торкатися області допустимих розв’язків, а не перетинати її.

Унаслідок цього в процесі знаходження оптимального розв’язку задачі достатньо обстежити тільки кутові точки многогранника області допустимих розв’язків.

Розглянемо геометричну інтерпретацію задач лінійного програмування.

Згідно з властивостями задач лінійного програмування цілком зрозуміло, що розв’язування лінійних задач зводиться до знаходження значення деякої лінійної функції на опуклій множині допустимих розв’язків.

У п-вимірному просторі це опуклі многогранники, у двовимірному (тобто на площині) – опуклі многокутники.

Якщо в математичній моделі кількість рівнянь т дорівнює кількості змінних п (тобто т = п), то існує єдиний розв’язок задачі, який можна знайти простим розв’язуванням системи рівнянь-обмежень задачі. І якщо розв’язок перебуває в невід’ємній області простору, тобто всі змінні , то такий розв’язок буде оптимальним.

Якщо п > т, то задача має множину допустимих розв’язків, з якої вибирають такий варіант, в якому досягається екстремальне значення вибраного критерію задачі.

Г еометрична інтерпретація множини розв’язків на площині зображено на рис.1.6.

множина усіх розв’язків для

область допустимих розв’язків

оптимальний розв’язок

Рис.1.6

На рис.1.6. бажано зобразити цільову функцію і її градієнт.

Нехай задано систему обмежень

та цільову функцію

за умов .

Умова невід’ємності обмежує область допустимих розв’язків першою координатною чвертю.

Кожну нерівність-обмеження можна записати у вигляді рівняння

яке поділяє невід’ємну область на дві частини, що зображуються півплощинами, замініть n на 2.

а точки, які перебувають на самій прямій

належать до одного з півпросторів, які відповідають нерівностям зі знаками „ ” чи „ ”.

У даному разі, тобто у випадку двовимірного простору, сукупність обмежень утворює фігуру опуклого многокутника. Графічно таку область зображено на рис.1.7.

Щодо задач з п змінними, то зобразити

многогранник п-вимірного простору

неможливо. Тому розв’язок таких задач

можна віддзеркалювати тільки аналітич-

ними методами, хоча ідея геометрично-

ного зображення аналогічна для будь-

Рис.1.7 якої кількості змінних задач.