3 Лекция

Цепь с параллельным соединением R, L, C. Активные, реактивные и полные проводимости. Символический метод расчета цепей синусоидального тока. Комплексные сопротивления и проводимости. Законы Ома и Кирхгофа в комплексной форме. Векторные диаграммы. Баланс мощностей.

Термины и определения основных понятий

Параллельное соединение (участков электрической цепи) - электрическое соединение, при котором рассматриваемые участки электрической цепи при­соединяются к одной паре узлов.

Активная (электрическая) проводимость - параметр пассивного двухполюсника, равный отношению активной мощности, поглощаемой в этом двухполюснике, к квадрату действующего значения электрического напряжения на его выводах.

Полная (электрическая) проводимость - параметр пассивного двухполюсника, равный отношению действующего значения электри­ческого тока через этот двухполюсник к действующему значению электрического напряжения между выводами двухполюсника при синусоидальных электрическом напряжении и электрическом токе.

Удельная (электрическая) проводимость - величина, характеризующая электропроводность вещества, скалярная для изотропного веще­ства и тензорная для анизотропного вещества, произведение которой на напряженность электри­ческого поля равно плотности электрического тока проводимости.

Теоретический материал Синусоидальный ток в цепи с параллельным соединением

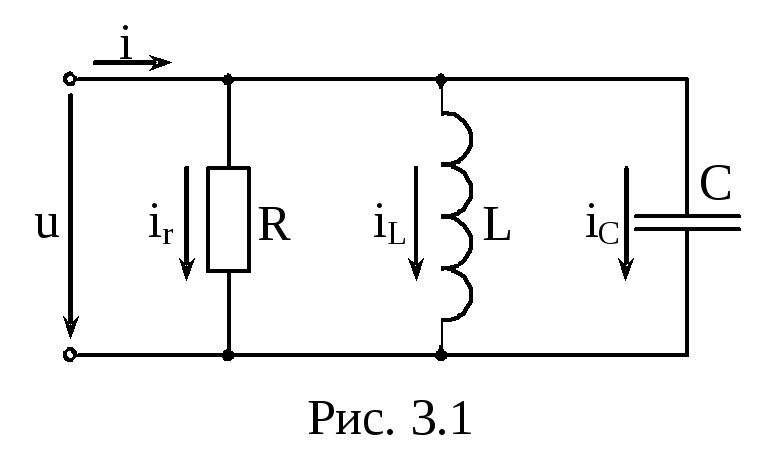
Дано:(рис. 3.1)

Найти:

Ток будем искать в виде

; ; ; .

По первому закону Кирхгофа:

;

;

.

обозначим – реактивная проводимость,

тогда: ; ;

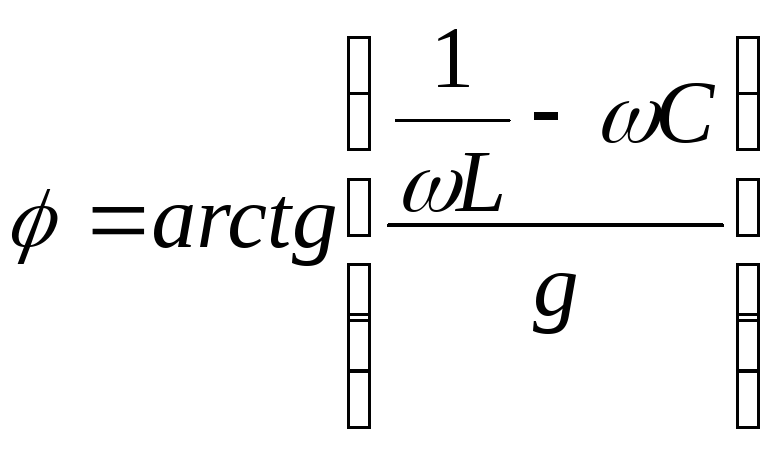Обозначим – полная проводимость цепи (рис. 3.2).

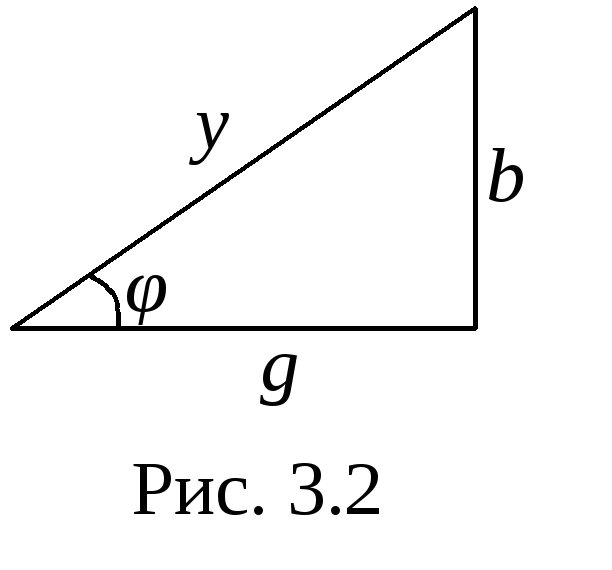
- треугольник проводимостей

С учётом принятых обозначений получим:

Если умножить все стороны треугольника проводимостей на амплитуд­ное (действующее) значение напряжения, то мы получим треугольник токов, у которого катеты называются активной и реактивной составляющей тока (рис 3.3).

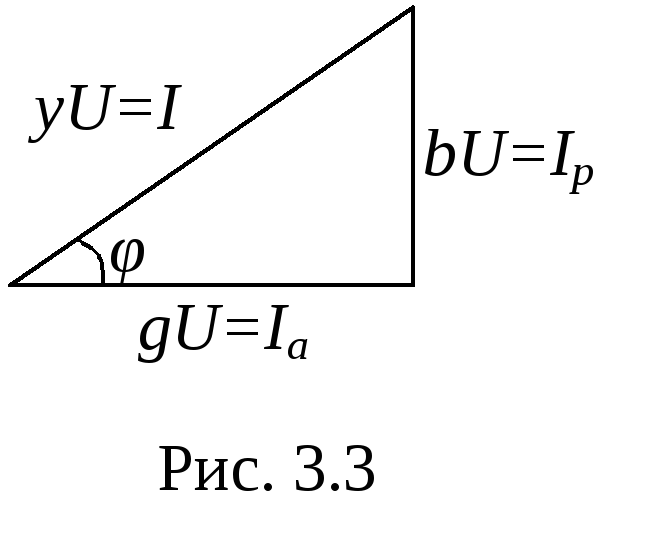
Учтем, что

,

,

.

Символический (комплексный) метод расчёта цепей синусоидального тока

В основе лежит метод замены синусоидальной функции вращающи­мися векторами. Это позволяет перейти от интегро-дифференциальных уравнений для мгновенных значений к алгебраическим, составленным относительно ком­плексов тока и напряжения.

Комплексные числа можно представить в трёх формах записи (рис. 3.4).

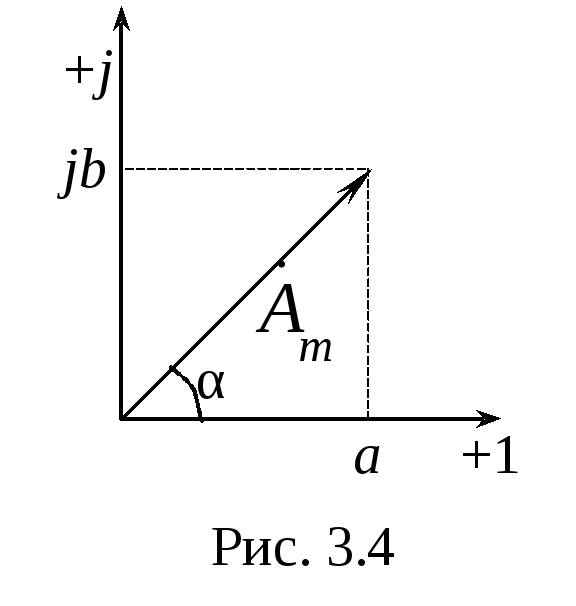
Изобразим вектор, вращающийся со скоростью в положительном направлении (против часовой стрелки) (рис. 3.5), тогда:

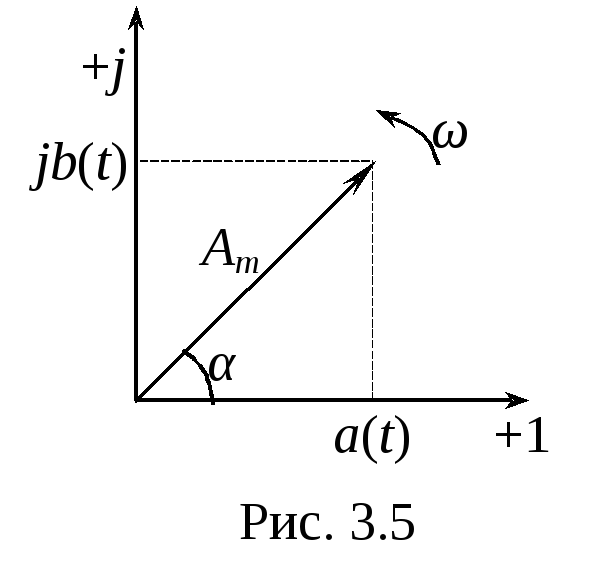
, где - оператор вращения

Умножение любого вектора на означает поворот на уголв положительном направлении.

–комплексная амплитуда.

Отсюда следует, что синусоидальный ток можно рассматривать как ли­нейную часть комплексной функции.

, где – комплексная амплитуда тока.

Иначе: Синусоидальному току может быть поставлена в соответствие комплексная функция.

Закон Ома и Кирхгофа в комплексной форме записи

Дано:(рис. 3.6)

Найти:

(1)

Поставим в соответствии синусоидальным функциям - комплексные.

,

Сложение, дифференцирование и интегрирование синусоидальных функций в уравнении (1) заменим теми же операциями над мнимыми частями комплексных функций.

, (2)

Операции дифференцирования и интегрирования мнимых частей ком­плексных функций и операция взятия линейной части взаимопереместимы, поэтому перепишем (2) в виде:

(3)

Уравнение (3) справедливо для любого момента времени, поэтому вы­ражения в скобках левой и правой части (3) равны. Проводя интегрирование и дифференцирование, получим:

(4)

Обозначим:

–комплексное сопротивление сопротивления

–комплексное сопротивление индуктивности

–комплексное сопротивление ёмкости

Тогда: , (5) – комплексная амплитуда напряже­ния на сопротивлении;

, (6) – комплексная ам­плитуда напряжения на индуктивности;

(7) – комплексная амплитуда напряжения на ёмкости;

Выражения (5, 6, 7) – закон Ома в комплексной форме записи для от­дельных элементов цепи.

С учетом введенных обозначений:

(8)

(4,8) – второй закон Кирхгофа в комплексной форме записи.

- реактивное сопротив­ление цепи

Обозначим: – входное комплексное сопротивление цепи.

–полное сопротив­ление цепи

.

(9) - закон Ома в комплексной форме записи для всей цепи.

,

После определения комплексной амплитуды осуществляем переход к мгновенному значению

– комплексные действующие значения
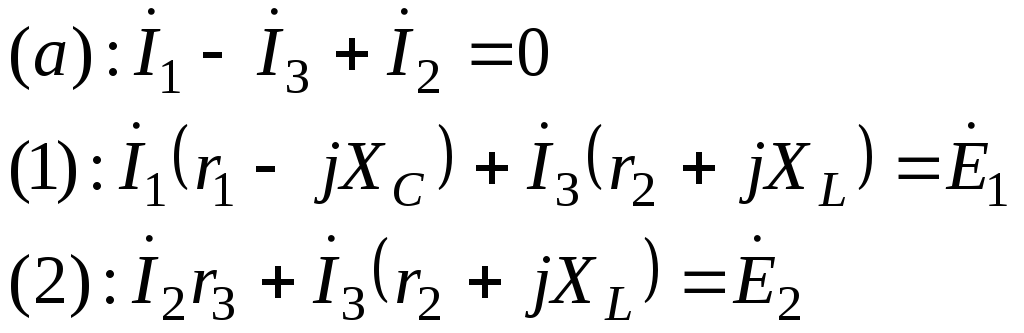