Среднее и действующее значение синусоидальных функций

Средним значением за период любой периодической функции называется интеграл

, где T - период

У любой гармонической функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площа­дью отрицательной. В этом случае пользуются средним значением за по­лупериод.

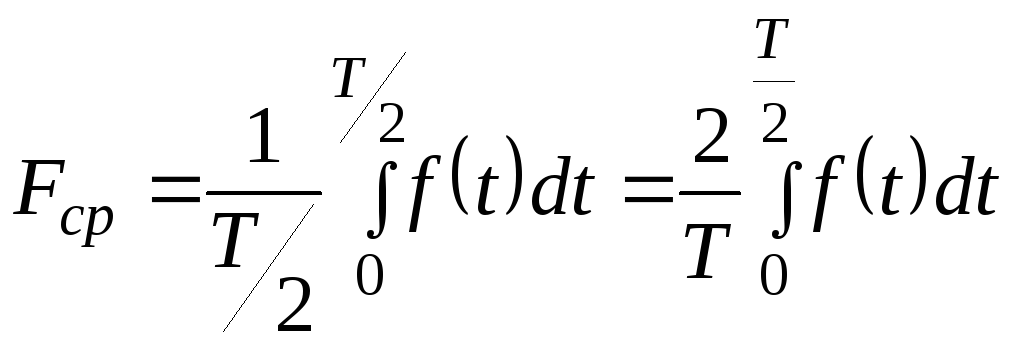
С последним значением совпадают среднее значение функции за пе­риод, взятой по абсолютной величине.

.

Пусть , тогда:

Приборы выпрямительной системы показывают среднее значение величин.

Приборы магнитоэлектрической системы, предназначены для измерения постоянного напряжения и тока.

Тепловое действие тока пропорционально квадрату тока и поэтому часто о величине переменного тока судят по так называемому средне квад­ратичному или действующему значению тока.

, , тогда:;

- действующее значение тока

Действующее значение показывают приборы электромагнитной, электродинамической, ферродинамической, электростатической систем.

Синусоидальный ток в сопротивлении

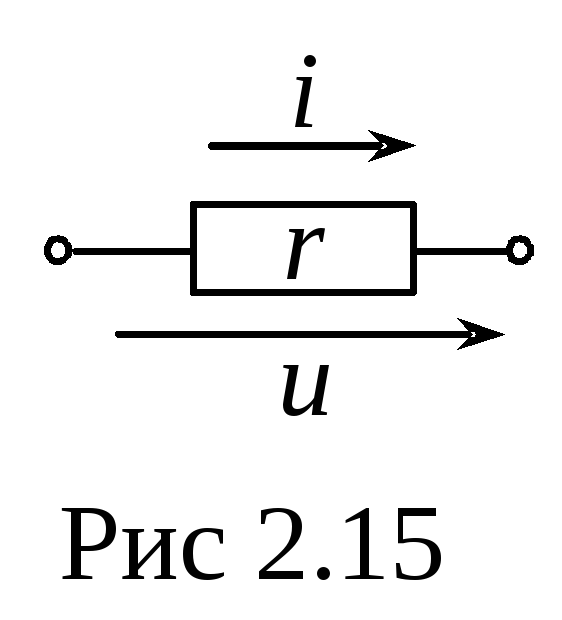
Дано: (рис 2.15).

Найти:

Только в частном случае сопротивления выпол­няется закон Ома для мгновенных значений напряже­ний и тока.

В сопротивлении напряжение и ток совпадают по фазе (рис 2.16).

Рис. 2.16

Мгновенная мощность в сопротивлении.

.

Среднее значение за период мгновенной мощности называется ак­тивной мощностью.

.

Синусоидальный ток в индуктивности.

Дано:, (рис. 2.17)

Найти:

;

Напряжение на индуктивности опережает ток на . Обозначим- реактивное сопротивление индуктивности.

- реактивная проводимость индуктивности, тогда

.

О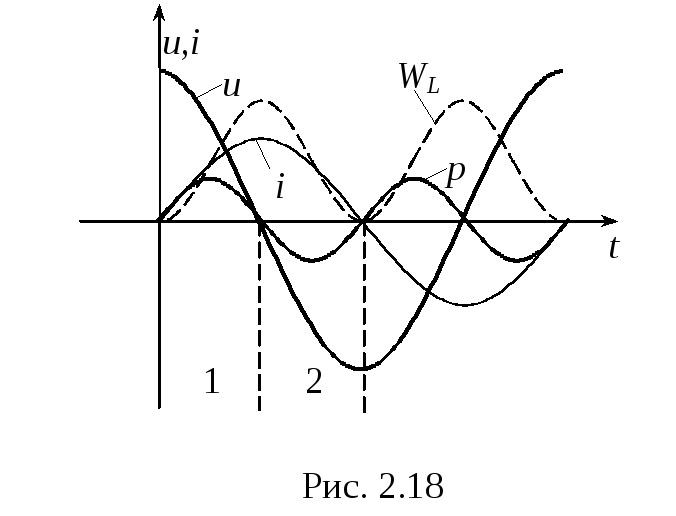тсюда следует, что амплитуда (действующее значение) напряжения и тока на индуктивности связаны соотношением подобным закону Ома.

; .

Частное деления напряжения на ток даёт некоторую функцию вре­мени не имеющую физического смысла и практического применения (рис.2.18).

Мгновенная мощность в индуктивности:

.

Активная мощность в индуктивности: .

Энергия магнитного поля индуктивности:

На первом интервале энергия поступает в цепь и временно запаса­ется в магнитном поле индуктивности. На втором интервале энергия воз­вращается в источник. Таким образом, в цепях с индуктивностью происхо­дит непрерывный колебательный процесс обмена энергией.

Синусоидальный ток в ёмкости

Д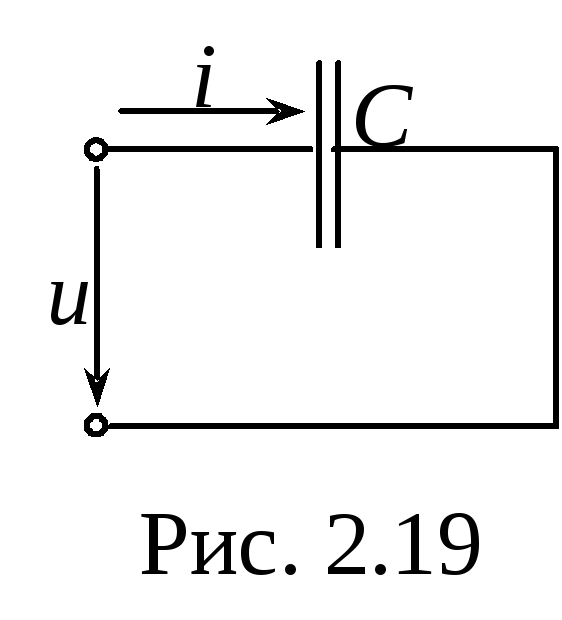ано:(рис.2.19).

Найти:

; .

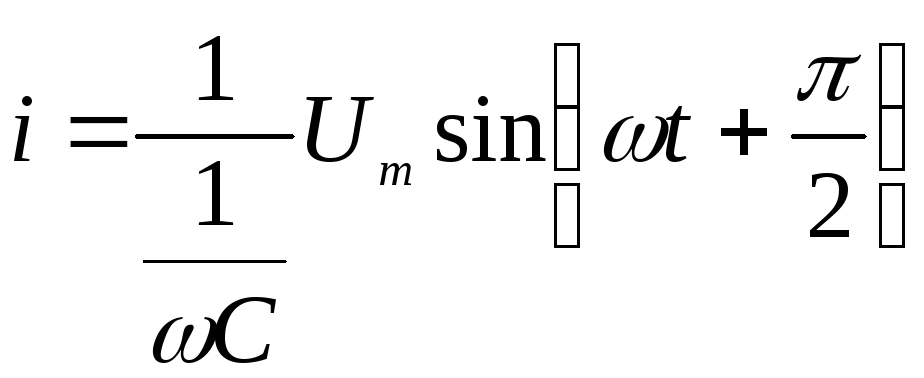Ток в ёмкости опережает напряжение на 90º (рис. 2.20)

Обозначим - реак­тивное сопротивление емкости- реактивная проводимость ёмкости.

Тогда: .

Амплитуды (действующие значения) напряжения и тока в ёмкости связаны соотношением подобным закону Ома.

Мгновенная мощность .

Энергия электрического поля ;

Синусоидальный ток в цепи r, l, c

Дано:

(рис. 2.21).

Найти:

Напряжение будем искать в виде

, ,,

На основании второго закона Кирхгофа:

, .

из тригонометрии:

, ;

Обозначим - реактивное сопротивление цепи.

, .

Отсюда видно, что . Обозначим-полное сопротивление цепи, тогда:

-соотношение подобное закону Ома.

треугольник сопротивлений (рис. 2.22)

;

Ели умножить все стороны треугольника со­противлений на действующее (амплитудное) значе­ние тока, то мы получим треугольник напряжений, в котором катеты – активная и реактивная составляю­щие входного напряжения (рис. 2.23).

- реактивная составляющая

- активная составляющая