Контрольные задания

501. Начальная фаза гармонических колебаний равна нулю. Через какую долю периода скорость точки будет равна половине её максимальной скорости?

502. Через сколько времени от начала движения точка, совершающая колебательное движение по уравнению x=7sin(0,5t) см, проходит путь от положения равновесия до максимального смещения?

503. Точка совершает гармонические колебания. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 2,5 мм.

504. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия 2,4 см, скорость точки равна 3 см/с, а при смещении 2,8 см скорость равна 2 см/с. Найти амплитуду и период этого колебания.

505. Чему равно отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии для моментов времени: а) t = T/12 , б) t=T/8 , в) t=T/6 ? Начальная фаза колебаний равна нулю.

506. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями x₁=0.02sin(5t+/2) м и x₂=0.03sin(5t+/4) м.

507. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и периодами получается результирующее колебание с тем же периодом и амплитудой. Найти разность фаз складываемых колебаний.

508. Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуды колебаний A₁=3 см и A₂=4 см. Найти амплитуду результирующего колебания, если: а) колебания совершаются в одном направлении, б) колебания взаимноперпендикулярны.

509. Найти амплитуду и начальную фазу колебаний, которые возникают при сложении следующих колебаний одного направления: x₁=3cos(t) см; x₂=5cos(t+/4) см; x₃=6sin(t) см.

510. Амплитуда гармонических колебаний точки A=2 см, полная энергия колебаний W=310^-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F=2,2510^-5 Н?

511. Точка совершает затухающие колебания с частотой =25 с^-1. Найти коэффициент затухания , если в начальный момент скорость точки равна нулю, а её смещение из положения равновесия в =1,02 раза меньше её амплитуды.

512. Осциллятор с временем релаксации =20 с в момент времени t=0 имеет начальное смещение x₀=10 cм. При каком значении начальной скорости V₀ это значение окажется равным амплитудному?

513. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на 9,8 см. Оттягивая этот груз и отпуская его, заставляют груз совершать колебания. Чему должен быть равен коэффициент затухания, чтобы логарифмический декремент затухания был равен шести?

514. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на 9,8 см. Оттягивая этот груз и отпуская его, заставляют груз совершать колебания. Чему должен быть равен коэффициент затухания, чтобы колебания прекратились через 10 с? Условно считать, что колебания прекратились, если их амплитуда упала до 1% от начальной величины.

515. Амплитуды смещения вынужденных гармонических колебаний при частотах ₁=400 с^-1 и ₂=600 с^-1 равны между собой. Найти частоту , при которой амплитуда смещения максимальна.

516. При частотах вынуждающей гармонической силы ₁=200 с^-1 и ₂=450 с^-1 амплитуда скорости частицы равна половине максимального значения. Найти частоту, соответствующую резонансу скорости.

517. При частотах вынуждающей гармонической силы ₁=200 с^-1 и ₂=450 с^-1 амплитуда скорости частицы равна половине максимального значения. Найти коэффициент затухания  и частоты  затухающих колебаний.

518. Амплитуда затухающих колебаний уменьшается в течение одного периода в 3 раза. На сколько процентов период колебаний больше, чем при отсутствии причины, вызывающей затухание?

519. Амплитуда смещения вынужденных колебаний при очень малой частоте А₀=2 мм, а при резонансе А=16 мм. Предполагая, что логарифмический декремент затухания меньше единицы, определить его.

520. Амплитуда смещения вынужденных колебаний при частотах вынуждающей силы, равных ₁=200 Гц и ₂=300 Гц, равны между собой. Найти частоту, соответствующую резонансу смещения.

521. Уравнение незатухающих колебаний дано в виде x=4sin 600t см. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний, через 0,01 с после начала колебаний. Скорость распространения колебаний 300 м/с.

522. Уравнение незатухающих колебаний дано в виде x=sin 2,5t см. Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20 м от источника колебаний в момент t=1 c после начала колебаний. Скорость распространения колебаний 100 м/с.

523. От источника колебаний распространяются волны вдоль прямой линии. Амплитуда колебаний A=10 см. Как велико смещение точки, удаленной от источника колебаний на четверть длины волны, в момент, когда от начала колебаний источника прошло время t=0,9T(периода колебаний)?

524. Волны с периодом T=1,2 c и с амплитудой колебаний A=2 см распространяются со скоростью V=15 м/с. Чему равно смещение точки, находящейся на расстоянии x=45 м. от источника волн, в тот момент, когда от начала колебаний прошло время t=4 c?

525. Уравнение плоской звуковой волны имеет вид =6010^‑6cos(1800t-53x). Найти: а) отношение амплитуды смещения частиц к длине волны; б) амплитуду колебаний скорости частиц среды и её отношение к скорости распространения волны.

526. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние l=/12 для момента t=T/6. Амплитуда колебаний A=0,05 м.

527. Звуковые колебания, имеющие частоту =0,5 кГц и амплитуду А=0,25 мм, распространяются в упругой среде. Длина волны =70 см. Найти: а) скорость V распространения волн; б) максимальную скорость частиц среды.

528. Плоская звуковая волна имеет период T=3 мс, амплитуду А=0,2 мм и длину волны =1,2 м. Для точек среды, удаленных от источника колебаний на расстояние x=2 м, найти: а) смещение (x, t) в момент t=7 мс; б) скорость и ускорение для того же момента времени, начальную фазу принять равной нулю. Определить разность фаз колебаний источника волн и точки среды, отстоящей на x=2 м от источник.

529. Задано уравнение плоской волны (x, t)=Acos(t-kx), где А=0,5 см, =628 с^-1; k=2 м^-1. Определить а) частоту колебаний  и длину волны ; б) фазовую скорость ; в) максимальные значения скорости и ускорения колебаний частиц среды; разность фаз  колебаний источника волн и точки среды, отстоящей на x=1 м от источника.

530. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии l=4 см, в момент времени t=T/6 равно половине амплитуды. Найти длину  бегущей волны.

531. Уравнение изменения силы тока в колебательном контуре со временем даётся в виде I=  0,02sin400t А. Индуктивность контура 1 Гн. Найти: а) период колебаний, б) емкость контура; в) максимальную разность потенциалов на обкладках конденсатора; г) максимальную энергию магнитного поля; д) максимальную энергию электрического поля.

532. Колебательный контур состоит из конденсатора емкостью 7 мкФ и катушки индуктивностью 0,23 Гн и сопротивлением 40 Ом. Конденсатор заряжен количеством электричества q=5,610^-4 Кл. Найти: а) период колебаний; б) логарифмический декремент затухания; в) значение разности потенциалов на обкладках конденсатора в момент времени T/2; T; 3T/2; 2T.

533. Колебательный контур состоит из конденсатора емкостью 0,2 мкФ и катушки индуктивностью 5,0710^-8 Гн. При каком логарифмическом декременте затухания разность потенциалов на обкладках конденсатора за 10^-3 с. уменьшится в три раза? Чему при этом равно сопротивление контура?

534. Ток в колебательном контуре зависит от времени как I = I_msin₀t, где I_m=9,0 мА, ₀=4,510⁴ c^-1. Емкость конденсатора C=0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент времени t = 0.

535. Колебательный контур состоит из конденсатора емкостью C = 4 мкФ, катушки с индуктивностью L=2 мГн и активным сопротивлением R=10 Ом. Найти отношение энергии магнитного поля катушки к энергии электрического поля конденсатора в момент максимума тока.

536. Колебательный контур содержит конденсатор ёмкостью C=8 пФ и катушку индуктивностью L=0,5 мГн. Каково максимальное напряжение U_max на обкладках конденсатора, если максимальная сила тока I_max=40 мА?

537. Колебательный контур состоит из конденсатора емкостью C=0,025 мкФ и катушки с индуктивностью L=1,015 Гн. Омическим сопротивлением катушки пренебречь. Конденсатор заряжен количеством электричества q=2,510^-6 Кл. Найти значение периода колебаний, а также энергии электрического и магнитного полей, а также полную энергию в момент времени Т/8.

538. В контуре, добротность которого Q=50 и собственная частота колебаний ₀=5,5 кГц, возбуждаются затухающие колебания. Через какое время энергия, запасенная в контуре, уменьшится в 2 раза?

539. Найти время, за которое амплитуда колебаний тока в контуре с добротностью Q=5000 уменьшится в 2 раза, если частота колебаний =2,2 МГц.

540. Найти отношение энергии W_м/W_эл магнитного поля колебательного контура и энергии его электрического поля в момент времени T/8.

541. Скорость распространения электромагнитных волн в некоторой среде составляет =2,510^-8 м/с. Определить длину электромагнитной волны в этой среде, если ее частота в вакууме ₀=1 МГц.

542. Электромагнитная волна с частотой =3 МГц переходит из вакуума в немагнитную среду с диэлектрической проницаемостью =4. Найти приращение ее длины волны.

543. Радиолокатор обнаружил в море подводную лодку, отраженный сигнал от которой дошел до него за время t=36 мкс. Учитывая, что диэлектрическая проницаемость воды =81, определить расстояние от радиолокатора до подводной лодки.

544. После того как между внутренним и внешним проводниками кабеля поместили диэлектрик, скорость распространения электромагнитных волн в кабеле уменьшилась на 55 %. Определить диэлектрическую проницаемость вещества прослойки.

545. Электромагнитная волна с частотой =200 кГц распространяется в немагнитной среде протяженностью 10 м. Время распространения волны в среде составляет 1 мс. Определить длину волны в этой среде и вакууме.

546. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны равна 10 В/м. Определить амплитуду напряженности магнитного поля волны.

547. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны равна 1 мА/м. Определить амплитуду напряженности электрического поля волны.

548. Плоская монохроматическая электромагнитная волна распространяется вдоль оси x. Определить энергию, перенесенную волной за время t=5 мин через площадку площадью 10 см², расположенную перпендикулярно оси x. Период волны T<<t. Амплитуда напряженности электрического поля волны E₀=510^-5 В/м, амплитуда напряженности магнитного поля волны H₀=210^-4 A/м.

549. В вакууме вдоль оси x распространяется плоская электромагнитная волна и падает по нормали на поверхность тела, полностью его поглощающего. Амплитуда напряженности магнитного поля волны равна 0,15 А/м. Определить давление, оказываемое волной на тело. Указание: давление равно среднему значению объемной плотности энергии в падающей электромагнитной волне.

550. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны равна 50 мВ/м. Определить интенсивность волны I, то есть среднюю энергию, проходящую через единицу поверхности в единицу времени.

551. В опыте Юнга пучок света, пройдя через узкую щель в непрозрачной преграде, падает на вторую преграду с двумя узкими щелями, находящимися на расстоянии d = 1 мм друг от друга. За преградой на расстоянии L=1 м располагается экран, на котором наблюдаются интерференционные полосы. Ширина полосы x равна: а) 0,65 мм для красного света и б) 0,45 мм для синего света. Чему равна длина световой волны ?

552. Расстояние между щелями в опыте Юнга d = 0,5 мм. Длина волны используемого монохроматического света  = 550 нм. Каково расстояние от щелей до экрана, если расстояние между соседними темными полосами на нем равно 1 мм?

553. На тонкую пленку (n = 1,33) падает параллельный пучок белого света. Угол падения =52. При какой толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в желтый цвет ( = 0,6 мкм)?

554. На поверхность стеклянного объектива (n₁ = 1,5) наносится тонкая пленка, показатель преломления которой n₂ = 1,2 («просветляющая» пленка). При какой наименьшей толщине d этой пленки произойдет максимальное ослабление отраженного света в средней части видимого спектра (от 400 до 700 нм)?

555. Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны  = 500 нм, падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластиной заполнено водой (n = 1,33). Найти толщину h слоя воды между линзой и пластиной в том месте, где наблюдается третье светлое кольцо в отраженном свете.

556. Найти радиус первого темного кольца Ньютона, если между линзой и пластиной налит бензол (n = 1,5). Радиус кривизны линзы 1 м. Показатели преломления линзы и пластины одинаковы и равны 1,65. Наблюдение ведется в отраженном свете с длиной волны  = 589 нм.

557. Найти расстояние между двадцатым и двадцать первым светлыми кольцами Ньютона, если расстояние между вторым и третьим равно 1 мм. Кольца наблюдаются в отраженном свете.

558. Определить радиус кривизны плосковыпуклой линзы, которая вместе с пластиной позволяет наблюдать кольца Ньютона при освещении монохроматическим светом с длиной волны  = 589 нм, причем в отраженном свете расстояние между первым и вторым светлыми кольцами равно 0,5 мм.

559. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном свете. Радиусы двух соседних темных колец равны 4 и 4,38 мм. Радиус кривизны линзы R = 6,4 м. Найти порядковые номера колец и длину волны  падающего света.

560. На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус третьего темного кольца (k = 3). Когда пространство между плоскопараллельной пластинкой и линзой заполнили жидкостью, то тот же радиус стало иметь кольцо с номером, на единицу большим. Определить показатель преломления n жидкости.

561. Точечный источник света с  = 500 нм помещен на расстоянии a = 0,5 м перед непрозрачной преградой с отверстием радиусом r = 0,5 мм. Определить расстояние b от преграды до точки, для которой число m открываемых зон Френеля будет равно: а) 1; б) 5; в) 10.

562. Между точечными источниками света и экраном поместим диафрагму с круглым отверстием, радиус которого можно изменять в процессе опыта. Расстояние от диафрагмы до источника и экрана равны a = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при радиусе отверстия r₁ = 1,00 мм и следующий максимум при r₂ = 1,29 мм.

563. На диафрагму с круглым отверстием диаметром d = 4 мм падает нормально параллельный пучок лучей монохроматического света с длиной волны  = 0,5 мкм. Точка наблюдения находится на оси отверстия на расстоянии b = 1 м от него. Сколько зон Френеля укладывается в отверстии? Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдения поместить экран?

564. Плоская световая волна ( = 0,5 мкм) падает нормально на диафрагму с отверстием диаметром d = 1 см. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: а) одну зону Френеля; б) две зоны Френеля?

565. Вычислить наибольший угол, на который может отклониться пучок монохроматического света дифракционной решеткой, имеющей 10000 штрихов при ширине решетки 4 см. Длина волны нормально падающего на решетку света  = 546 нм.

566. Свет, падающий на дифракционную решетку нормально, состоит из двух резких спектральных линий с длинами волн ₁ = 490 нм (голубой свет) и ₂ = 600 нм (оранжевый свет). Первый дифракционный максимум для линии с длиной волны ₁ располагается под углом ₁=10^О. Найти угловое расстояние  между линиями в спектре 2-го порядка.

567. Какой наименьшей разрешающей способностью R должна обладать дифракционная решетка, чтобы с ее помощью можно было разрешить две спектральные линии с длинами волн 578 и 580 нм? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

568. Длины волн двух спектральных линий натрия равны ₁ = 588,995 нм и ₂ = 589,592 нм. Какую ширину должна иметь дифракционная решетка, содержащая 600 штрихов на 1 мм, чтобы разрешить эти линии в спектре первого порядка?

569. На дифракционную решетку, содержащую 500 штрихов на 1 мм, падает нормально к ее поверхности белый свет. Спектр проецируется на экран линзой, помещенной вблизи решетки. Определить ширину спектра первого порядка на экране, если расстояние от линзы до экрана равно 3 м. Границы видимости спектра _кр = 780 нм, _фиол = 400 нм.

570. Какое фокусное расстояние F должна иметь линза, проектирующая на экран спектр, полученный при помощи дифракционной решетки, чтобы расстояние между двумя линиями с длинами волн ₁ = 404,4 нм и ₂ = 404,7 нм в спектре первого порядка было равным 0,1 мм? Период решетки d=2 мкм.

571. Найти угол полной поляризации при отражении света от стекла, помещенного в воду. Показатели преломления стекла и воды равны 1,57 и 1,33 соответственно.

572. Найти показатель преломления стекла, если при отражении от него света отраженный луч будет полностью поляризован при угле преломления 30^О.

573. Предельный угол полного внутреннего отражения для некоторого вещества равен 45. Найти для этого вещества угол полной поляризации.

574. Алмазная пластинка находится в некоторой среде показателем преломления n. Луч естественного света падает на пластинку под углом 60^О к нормали. Определить показатель преломления n среды, если отраженный луч максимально поляризован. Показатель преломления алмаза равен 2,42.

575. Угол полной поляризации при отражении света от кристалла каменной соли равен 57^О. Определить скорость  распространения света в этом кристалле.

576. Найти угол  между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, проходящего через поляризатор и анализатор, уменьшается в 4 раза.

577. Угол между главными плоскостями поляризатора и анализатора равен 45^O. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до 60^О?

578. Луч естественного света падает на систему из шести поляризаторов, главная плоскость каждого из которых повернута на угол =30^О относительно главной плоскости предыдущего поляризатора. Какая часть светового потока проходит через эту систему?

579. Во сколько раз ослабляется свет, проходя через два поляризатора, главные плоскости которых составляют угол 60^О, если в каждом из поляризаторов в отдельности теряется 10 % падающего на него светового потока?

580. Естественный свет проходит через поляризатор и анализатор, поставленные так, что угол между их главными плоскостями равен . Как поляризатор, так и анализатор поглощают и отражают 8 % падающего на них света. Оказалось, что интенсивность луча, вышедшего из анализатора, равна 9 % интенсивности естественного света, падающего на поляризатор. Найти угол .

Варианты контрольных заданий.

Номер варианта	Номера задач.
1	501	511	521	531	541	551	561	571
2	502	512	522	532	542	552	562	572
3	503	513	523	533	543	553	563	573
4	504	514	524	534	544	554	564	574
5	505	515	525	535	545	555	565	575
6	506	516	526	536	546	556	566	576
7	507	517	527	537	547	557	567	577
8	508	518	528	538	548	558	568	578
9	509	519	529	539	549	559	569	579
10	510	520	530	540	550	560	570	580

КОНТРОЛЬНАЯ РАБОТА № 6

Тема: Квантовая физика

Тепловое излучение

Тепловым излучением называется испускание электромагнитных волн за счет внутренней энергии тел. Оно имеет место при любой температуре. Приведем величины, характеризующие этот вид излучения

- энергетическая светимость - величина, равная энергии, испускаемой единицей поверхности тела в единицу времени по всем направлениям. Она является функцией температуры.

- спектральная плотность энергетической светимости - величина, равная энергии, испускаемой единицей поверхности тела в единицу времени по всем направлениям в единичном интервале длин волн. Это функция длины волны и температуры.

- поглощательная способность - безразмерная величина, равная отношению потока энергии, поглощенной телом, к потоку энергии, падающей на тело при данной температуре и длине волны.

Тело, полностью поглощающее упавшее на него излучение всех длин волн, называется абсолютно черным (a_,T  1)

Закон Кирхгофа. Отношение спектральной плотности энергетической светимости к поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией длины волны и температуры:

. (1)

Экспериментально найденная с помощью изучения излучения абсолютно черного тела функция Кирхгофа имеет вид, приведенный на рис. 1.

Теоретически вид функции Кирхгофа нашел Планк, предположивший, что излучение испускается излучающими телами не непрерывно, а определенными порциями - квантами. Энергия каждого кванта

, (2)

где - постоянная Планка, Джс

 - круговая частота колебаний в электромагнитной волне.

Формула Планка имеет вид

(3)

Как следует из закона Кирхгофа, f(,T)  r_,T

для абсолютно черного тела.

Закон Стефана – Больцмана. Энергетическая светимость абсолютно черного тела прямо пропорциональна четвертой степени его абсолютной температуры.

R_T=T⁴ , (4)

Где  - постоянная Стефана – Больцмана:

Закон смещения Вина. Длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его абсолютной температуре. (рис. 1):

_max=b/T , (5)

где b - постоянная Вина, b =2,910^-3 мК.

Фотоны

Световые кванты, то есть частицы в виде которых распространяется свет, получили название фотонов. Они обладают энергией ( формула 2), массой

, (6)

импульсом или , (7)

где - волновой вектор – вектор, модуль которого равен волновому числу, а направление совпадает с направлением фазовой скорости световой волны.

Взаимодействием фотонов с веществом объясняется ряд явлений и эффектов.

Фотоэффект

Внешним фотоэффектом называется испускание электронов с поверхности металлов под действием света. Фотоэффект объясняется взаимодействием фотонов со свободными электронами металлов.

Уравнение Эйнштейна для фотоэффекта:

= + , (8),

где А_вых - работа выхода электрона из металла (табличная величина);

- максимальная кинетическая энергия электрона.

Из уравнения (8) следует, что фотоэффект возможен только при условии

A_вых , или

, (9)

где ₀ называется красной границей фотоэффекта.

Для торможения вылетающих электронов необходимо приложить задерживающее напряжение U_з , которое можно найти из условия

m_m²/2=eU₃ , (10)

где e - заряд электрона.

Давление света

Тот факт, что свет оказывает давление на поверхность, на которую он падает, просто объясняется передачей фотонами этой поверхности некоторого импульса. Тогда формула для светового давления имеет вид

P = w(1+) , (11)

где w - объемная плотность энергии излучения, падающего на тело,  - коэффициент отражения. w можно представить как w=I/c. Здесь I - интенсивность падающего света (плотность потока энергии излучения), с - скорость света.

Тормозное рентгеновское излучение.

Рентгеновские лучи возникают при бомбардировке быстрыми электронами твердых мишеней (анода рентгеновской трубки). Появляющееся при этом так называемое тормозное излучение имеет сплошной спектр с четко выраженной коротковолновой границей. Существование коротковолновой границы вытекает из квантовой природы излучения.

, (12)

где - энергия фотона, eU - энергия электрона, теряемая при торможении.

Из выражения (12) следует, что частота излучения не может превысить значения _max=eU/ , а длина волны не может быть меньше значения

. (13)

Эффект Комптона.

Квантовые свойства света особенно отчетливо проявляются в эффекте Комптона. Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны  содержатся также лучи большей длины волны .Разность=оказалась зависящей только от угла , образуемого направлением рассеянного пучка с направлением первичного пучка. От длины волны  и от природы рассеивающего вещества  не зависит.

Данный эффект можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами вещества.



hk’

mV

hk

Рис. 2

При этом выполняются закон сохранения импульса (рис. 2)

(14)

где - импульс фотона до столкновения,

- импульс фотона после столкновения.

- импульс электрона после столкновения

и закон сохранения энергии

, (15)

где - энергия фотона до столкновения, m₀c² - энергия покоя электрона, - энергия фотона после столкновения, mc² - полная энергия электрона после столкновения.

Совместно решая уравнения (14) и (15) получим

=_c(1-cos) , (16)

где - комптоновская длина волны электрона.

Боровская теория атома водорода

Теория атома, предложенная Н.Бором, основана на двух постулатах.

1. Электрон в атоме может находиться только в одном из дискретных стационарных состояний, удовлетворяющих правилу квантования . При этом излучение и поглощение энергии не происходит.

2. Излучение испускается или поглощается в виде светового кванта энергии при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается квантовый скачок электрона:

. (17)

Применение этих постулатов для расчета параметров атома водорода позволило найти:

1) радиусы стационарных орбит

; (18)

2) cкорости движения электронов на этих орбитах

; (19)

3) энергии стационарных состояний атомов

; (20)

4) длины волн спектральных линий, возникающих при переходах электрона из одного стационарного состояния (с номером n₁) в другое (с номером n₂):

, (21)

где - постоянная Ридберга.

При этом возникает несколько спектральных серий (групп линий) в зависимости от номера энергетического уровня n₂, на который переходит электрон:

n₂ = 1 - серия Лаймана,

n₂ = 2 - серия Бальмера,

n₂ = 3 - серия Пашена,

n₂ = 4 - серия Брэккета.

Элементы квантовой механики

Гипотеза де Бройля

В 1924 году Луи де Бройль выдвинул гипотезу, что корпускулярно - волновой дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение. По идее де Бройля движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого

, (22)

а частота . (23)

Данная гипотеза подтверждена экспериментально и в настоящее время считается установленным фактом.

Соотношение неопределенностей.

Своеобразие свойств микрочастиц проявляется в том, что не для всех динамических переменных, характеризующих состояние микрочастицы, получаются при измерениях определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса р_x. Неопределенности значений x и р_х удовлетворяют соотношению

. (24)

Из этого следует, что чем меньше неопределенность одной из переменных (х или P_x), тем больше неопределенность другой.

Соотношение, аналогичное (24) имеет место для y и р_y, для z и p_z, а также для ряда других пар величин, называемых канонически сопряженными.

Например, энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей

. (25)

Это соотношение означает, что определение энергии с точностью Е должно занять интервал времени t, не меньший, чем определяемый соотношением (25).

Уравнение Шредингера. Волновая функция

Состояние микрочастицы в квантовой механике характеризуется так называемой волновой функцией, обозначаемой буквой  пси. Вид этой функции получается из решения уравнения Шредингера, которое выглядит следующим образом:

. (26)

Здесь m - масса частицы, U - ее потенциальная энергия, i - мнимая единица,

 - оператор Лапласа, =(x,y,z,t) - функция координат и времени.

. (27)

Если силовое поле, в котором движется частица, стационарно, т.е. U не зависит явно от времени, то уравнение (26) переходит в более простое уравнение Шредингера для стационарных состояний:

. (28)

Здесь =(x,y,z) - функция координат.

Решения данного уравнения и рассматривает квантовая механика.

Правильную интерпретацию смысла волновой функции дал М.Борн в 1926 г. Согласно Борну квадрат модуля волновой функции дает плотность вероятности нахождения частицы в соответствующем месте пространства.

. (29)

В соответствии с этим для волновой функции должно выполняться условие нормировки

. (30)

В соответствии со своим смыслом волновая функция должна быть однозначной, конечной, непрерывной и иметь непрерывную и конечную производную. Совокупность этих требований носит название стандартных условий.

Уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям, лишь при некоторых избранных значениях параметра Е (т.е. энергии). Эти избранные значения называются собственными значениями энергии. Решения, соответствующие собственным значениям Е, называются собственными функциями частицы. Совокупность собственных значений называется энергетическим спектром. Он может быть дискретным или сплошным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать:

E₁, E₂, ... E_n, ...; (31)

₁, ₂, ... _n, ... .

Нахождение собственных значений энергии и собственных функций частиц является основной задачей квантовой механики.

Применения уравнения Шредингера

U=

U=

0

l

x

а) Частица в бесконечно глубокой одномерной потенциальной яме

Предположим, что частица может двигаться только вдоль оси х, и ее движение ограничено непроницаемыми стенками в точках х=0 и х=l.

Зависимость потенциальной энергии от координат имеет в этом случае следующий вид (рис. 3):

(32)

Поскольку волновая функция в данном случае зависит только от координаты х, уравнение Шредингера упрощается следующим образом:

. (33)

Решая уравнение (33) с использованием стандартных условий, можно получить собственные значения энергии частицы

(34)

Энергетический спектр, как следует из (34), является дискретным. При этом расстояние между соседними энергетическими уровнями не является постоянным, а увеличивается с увеличением номера энергетического уровня. Нормированные собственные функции частицы в этом случае имеют вид

Графики этих функций показаны на рис. 4.

На рис. 5 дана зависимость плотности вероятности обнаружения частицы от координаты x на различных расстояниях от стенок ямы, равная ^*.

б) Прохождение частиц через потенциальный барьер

E

U₀

U

0

l

x

Пусть частица с энергией Е, движущаяся слева направо вдоль оси х, встречает на своем пути потенциальный барьер высоты U₀ и шириной l (рис. 6). Из решения уравнения Шредингера в этом случае вытекает, что, во-первых, даже при Е> U₀

имеется отличная от нуля вероятность того, что частица отразится от барьера. Во-вторых, при Е<U₀ имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области, где х > l. Вероятность прохождения частицы через барьер может быть названа коэффициентом прозрачности D. Расчеты показывают, что в данном случае

. (36)

Для потенциального барьера произвольной формы (рис. 7) формула (36) должна быть заменена более общей формулой

, (37)

где U=U(x).

При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере ( рис. 7), в связи с чем это явление называют

туннельным эффектом.

Ядерная физика.

Состав и характеристика атомного ядра.

Ядра атомов состоят из двух видов элементарных частиц - протонов и нейтронов. Эти частицы носят название нуклонов.

Протон (р) - ядро атома водорода. Он обладает зарядом +e и массой

m_p = 1.67210^-27кг (энергия покоя Е_0р = 938.2 МэВ).

Нейтрон (n) - не обладающая электрическим зарядом частица с массой

m_n = 1.67510^-27кг (энергия покоя Е_0п = 939.5 МэВ).

Количество протонов z, входящих в состав ядра, определяет его заряд и называется зарядовым числом ядра.

Число нуклонов А в ядре называется массовым числом ядра. При превращениях ядер зарядовое и массовое числа сохраняются.

Для обозначения ядер применяют символ ,где под X подразумевается химический символ элемента. Вверху ставится массовое число, внизу - атомный номер (зарядовое число).

Масса ядра m_я всегда меньше суммы масс входящих в него частиц. Это обусловлено тем, что при объединении в ядро выделяется энергия связи нуклонов друг с другом. Энергия связи Е_св равна той работе, которую нужно совершить, чтобы разделить образующие ядро нуклоны и удалить их друг от друга на такие расстояния, при которых они практически не взаимодействуют друг с другом. Согласно закону взаимосвязи массы и энергии энергия связи нуклонов в ядре

. (38)

Радиоактивность.

Радиоактивностью называется самопроизвольное превращение одних атомных ядер в другие, сопровождаемое испусканием элементарных частиц. К числу радиоактивных процессов относятся 1) -распад, 2) -распад, 3) -излучение ядер, 4) спонтанное деление тяжелых ядер, 5) протонная радиоактивность.

Закон радиоактивного превращения выражается формулой

N=N₀e^-t , (39)

где N₀ - количество ядер в начальный момент времени, N - количество нераспавшихся ядер в момент времени t,  - характерная для радиоактивного вещества константа, называемая постоянной распада.

Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада Т_1/2. Из (39) следует, что

T_1/2=(ln2)/ . (40)

Активностью радиоактивного препарата А называется число распадов, происходящих в препарате за единицу времени:

A=dN_расп/dt=N . (41)

Альфа-распад

Альфа лучи представляют собой поток ядер гелия . Распад протекает по схеме

. (42)

Из схемы распада видно, что атомный номер дочернего ядра Y на две единицы, а массовое число на четыре единицы меньше, чем у исходного (материнского) ядра Х.

Бета-распад

Наиболее распространенный вид -распада - электронный распад - протекает по схеме

. (43)

Из схемы видно, что дочернее ядро имеет атомный номер, на единицу больший, чем у материнского ядра, массовые числа обоих ядер одинаковы. Наряду с электроном испускается также антинейтрино .

Ядерные реакции

Ядерной реакцией называется процесс сильного взаимодействия атомного ядра с элементарной частицей или с другим ядром, приводящий к преобразованию ядра (или ядер). Взаимодействие реагирующих частиц возникает при их сближении до расстояний порядка 10^-15м благодаря действию ядерных сил.

Наиболее распространенным видом ядерной реакции является взаимодействие легкой частицы а с ядром X, в результате которого образуется легкая частица b и ядро Y:

Х + а  Y + b

Уравнение таких реакций принято записывать сокращенно в виде

Х(а,b)Y (44)

В качестве легких частиц а и b могут фигурировать нейтрон (n), протон (р), дейтрон (d), -частица () и -фотон ().

Ядерные реакции могут сопровождаться как выделением, так и поглощением энергии. Количество выделяющейся энергии Q называется энергией реакции.

Она определяется разностью масс исходных и конечных ядер (частиц)

, (45)

где  m₁ - сумма масс ядер, вступающих в реакцию.

 m₂ - сумма масс ядер, получившихся в результате реакции.

Если сумма масс, образующихся ядер, превосходит сумму масс исходных ядер, реакция идет с поглощением энергии и энергия реакции будет отрицательной (Q<0).

Примеры решения задач.

Дано:

T=5800 K

t=1 мин

Найти:

R_э, Ф_э, _max, W

1. Считая излучение Солнца близким к излучению абсолютно черного тела, определить энергетическую светимость Солнца, поток энергии, излучаемый Солнцем, длину волны, на которую приходится максимум спектральной плотности энергетической светимости и энергию, излучаемую Солнцем за 1 минуту. Температура поверхности Солнца принять равной 5800К.

Решение:

а) По закону Стефана-Больцмана определим энергетическую светимость Солнца:

R_э = T⁴,

где , R_э=6,4210⁷ Вт/м².

б) Поток энергии, излучаемый Солнцем, найдем, умножив энергетическую светимость на площадь поверхности Солнца: Ф_э=R_эS=R_э4R_c², где R_c=6,9510⁸ м - радиус Солнца.

Ф_э=3,910²⁶ Вт.

в) Длину волны, на которую приходится максимум спектральной плотности энергетической светимости, найдем из закона смещения Вина:

_max=b/T, где b=2,310^-3 мК,

_max=510^-7 м=500 нм.

г) Энергия, излучаемая Солнцем за время t, будет равна W=Ф_эt.

Для t=1 мин, W2,3410²⁸ Дж.

Дано:

N=600 Вт

r=1м

d=2 см

Найти: F

2. Поток энергии, излучаемый электрической лампой, N=600 Вт. На расстоянии r=1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d=2 см. Принимая лампу за точечный источник, определить силу F светового давления на зеркальце.

Решение:

Если принять лампу за точечный источник, то следует считать, что излучение лампы одинаково во всех направлениях. То есть энергия, излучаемая лампой за одну секунду, на расстоянии r от нее равномерно распределится по поверхности сферы радиусом r. Тогда плотность потока энергии излучения

.

Для определения светового давления на зеркальце используем следующую формулу:

,

где с=310⁸ м/с - скорость света в вакууме,  - коэффициент отражения света (для зеркальных поверхностей, если нет специальных указаний, считать =1).

Силу светового давления определим, умножив давление света на площадь поверхности зеркальца (d²/4):

Дано:

=180⁰

₁=0,255 МэВ

Найти: _e/₁

3. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол =180^О? Энергия фотона до рассеяния равна 0, 255 МэВ.

Решение:

Обозначим ₁ и ₂ энергии фотона до и после рассеяния соответственно; ₁ и ₂ - длина волн соответствующих фотонов.

Для установления связи между энергиями фотона до и после рассеяния воспользуемся формулой Комптона

, так как cos180^О = -1.

Энергия фотона  = h = hc/. Отсюда ₁ = hc/₁ и ₂ = hc/₂.

После подстановки в формулу Комптона получим



Разделим последнее равенство на hc и обозначим энергию покоя электрона mc² = E₀.

1/₂ - 1/₁ = 2/E₀.

Часть первоначальной энергии фотона ₁ приходится на электрон отдачи _е, а другая - на рассеянный фотон ₂:

₁ = _е+₂ .

С учетом последнего равенства получим:

.

Умножим на ₁:

Решая последнее уравнение, получаем

Дано:

=94 нм

Найти: n

4. Атом водорода освещается излучением с длиной волны 94 нм. Определить, какие спектральные линии появятся в спектре атома водорода.

Решение:

При возбуждении атома электрон в атоме переходит из основного состояния (m=1) в состояние с главным квантовым числом n, которое можно определить по формуле:

1/=R(1/m² - 1/n²) .

(округляем до меньшего целого).

Серия Брэккета

Серия Пашена

Серия Бальмера

Серия Лаймана

Таким образом, при обратном переходе с 5-го уровня электроны могут переходить на 1, 2, 3, 4-й уровни. Этим переходом будут соответствовать определенные спектральные линии:

Всего будет наблюдаться 10 линий:

4 линии в серии Лаймана;

3 - в серии Бальмера;

2 - в серии Пашена;

1 - в серии Брэккета.

5. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=0,5 кВ. Принимая, что неопределенность импульса равна 0,1 % от его численного значения, найти неопределенность координаты электрона. Являются ли в данных условиях электроны квантовыми или классическими частицами?

Дано: U = 0,5 кВ px=0,001px

Найти: x

Решение:

Согласно соотношению неопределенностей

xp_x  h, (1)

где x - неопределенность координаты электрона; p_x - неопределенность проекции его импульса; h=6,6310^-34 Джс - постоянная Планка. Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U:

T = |e|U = 0,5 кэВ,

то есть электрон при данных условиях не является релятивистской частицей, и импульс электрона

.

Согласно условию задачи, неопределенность импульса p_x=0,001p_x=1,2410^-26 кгм/с, то есть p_x=0,001p_x=1,2410^-26 кгм/с, то есть p_x<<p_x, и электрон при данных условиях является классической частицей.

Искомая неопределенность координаты из выражения (1)

.

.

Дано:

l=200 пм

n=4

x₁=0, x₂=l/4

Найти: E_min, W

6. Электрон в одномерной прямоугольной «потенциальной яме» шириной l = 200 пм с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 4). Определить: 1) минимальную энергию электрона; 2) вероятность W обнаружения электрона в первой четверти «ямы».

Решение:

Собственное значение энергии электрона, находящегося на n-м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»:

,

где m=9,1110^-39 кг - масса электрона; - постоянная Планка.

Минимальную энергию электрон имеет при минимальном n, то есть при n = 1:

.

Вероятность обнаружить частицу в интервале x₁<x<x₂:

где - нормированная собственная волновая функция, соответствующая данному состоянию.

Возбужденному состоянию n=4 отвечает собственная функция

.

Тогда по условию задачи,

.

Заменив sin²(4x/l)=1/2(1-cos(8x/l)), запишем

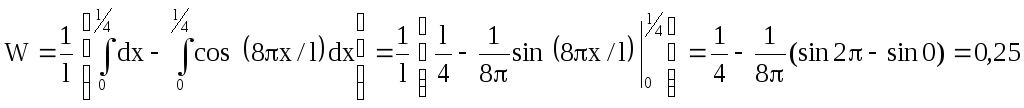
График зависимости

7. Первоначальная масса радиоактивного изотопа радона (период полураспада T_1/2=3,82 сут.) равна 1,5 г. Определить: 1) начальную активность изотопа ; 2) его активность через 5 суток.

Дано: m0=1,5 г T1/2=3,82 сут t=5 сут

Найти: A0 , A

Решение:

Начальная активность изотопа

A₀=N₀,

где - постоянная радиоактивного распада; N₀-число ядер изотопа в начальный момент времени.

,

где M - молярная масса радона (M=22210^-3 кг/моль); N_A - число Авогадро, равное 6,0210²³ моль^-1. Учитывая это выражение, найдем искомую начальную активность изотопа

Активность изотопа A=N, где, согласно закону радиоактивного распада, N=N₀e^-t - число нераспавшихся ядер в момент времени t. Учитывая N₀=A₀, найдем, что активность нуклида уменьшается со временем по закону:

A=A₀e^-t=.

8. В результате соударения дейтрона с ядром бериллия образовалось новое ядро и нейтрон. Определить порядковый номер и массовое число образовавшегося ядра, записать ядерную реакцию и определить ее энергетический эффект.

Дано:

Найти: Z, A, Q

Решение:

Из законов сохранения электрического заряда и массовых чисел следует, что Z=5, A=10, то есть образовавшееся в результате ядерной реакции ядро - изотоп бора . Поэтому ядерную

реакцию можно записать в виде

Энергетический эффект реакции

, (1)

где в первых круглых скобках указаны масса исходных ядер, во вторых - массы ядер продуктов реакции.

с=310⁸ м/с.

Вычисляя, получим Q = 4,84 МэВ, энергетический эффект положительный; реакция экзотермическая.

Задачи для самостоятельного решения.

1. Определить энергию, излучаемую за 1 минуту из смотрового окошка площадью 8 см² плавильной печи, если ее температура 1200К.

Ответ: W=5,65 кДж.

2. Определить красную границу _кр фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны =400нм максимальная скорость фотоэлектронов _max=0,65 Мм/с

Ответ: _кр=651 нм.

3. Определить минимальную длину волны в сплошном спектре рентгеновских лучей, если рентгеновская трубка работает под напряжением U=30 кВ.

Ответ: _min= 41 пм.

4. Определить энергию фотона, соответствующего второй линии в первой инфракрасной серии (серии Пашена) атома водорода.

Ответ: =0,97 эВ.

5. Определить длину волны де Бройля _Б электрона, прошедшего ускоряющую разность потенциалов U=700 кВ является ли электрон при этих условиях релятивистской частицей? (энергия покоя электрона E₀ = m₀c² = 0,512 МэВ, m₀ = 9,1110^-31 кг, с = 310⁸ м/с, е = 1,610^‑19 Кл).

Ответ: _Б=1,13пм. Это релятивистский случай.

.

6. Две частицы, электрон и протон, обе с энергией Е=5эВ, движутся в положительном направлении оси x, встречая на своем пути потенциальный барьер высотой U=10эВ и ширины l=1пм. Определить отношение вероятностей прохождения частицами этого барьера.

,

где m_e=9,1110^-31 кг; m_p=1,67210^-27 кг;

7. Какой изотоп образуется из радиоактивного изотопа ₃Li⁸ после одного -распада и одного -распада?

Ответ: ₂He⁴.

8. Написать недостающие обозначения в следующих ядерных реакциях:

Ответ:

Контрольные задания

601. Определить температуру, при которой энергетическая светимость черного тела равна 10 кВт/м².

602. Определить относительное увеличение R_э /R_э энергетической светимости черного тела при увеличении его температуры на 1 %.

603. Во сколько раз надо увеличить абсолютную температуру черного тела, чтобы его энергетическая светимость возросла в два раза?

604. Найти величину солнечной постоянной, т.е. количество лучистой энергии, посылаемой Солнцем ежеминутно через площадку в 1 см², перпендикулярно к солнечным лучам и находящуюся на таком же расстоянии от него, что и Земля.

605. Мощность излучения абсолютно черного тела равна 10 кВт. Найти площадь излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности его энергетической светимости, равна 710^-7 м.

606. На какую длину волны приходится максимум спектральной плотности энергетической светимости черного тела при температуре t = 0 C ?

607. Определить температуру черного тела, при которой максимум спектральной плотности энергетической светимости приходится на красную границу видимого спектра  = 750 нм.

608 При увеличении абсолютной температуры черного тела в два раза (T₂=2T₁) длина волны, на которую приходится максимум спектральной плотности энергетической светимости, уменьшилась на 400 нм. Определить начальную и конечную температуры T₁ и T₂.

609. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, равна 0,85 мкм. Определить энергетическую светимость тела.

610. Температура абсолютно черного тела изменилась от 727 С до 1727 С. Во сколько раз при этом изменилась мощность излучения?

611. Определить работу выхода для натрия в электрон вольтах, если красная граница фотоэффекта для него _кр = 500 нм.

612. Будет ли наблюдаться фотоэффект, если на поверхность серебра направить ультрафиолетовое излучение с длиной волны 300 нм?

613. На поверхность лития падает монохроматический свет с длиной волны 310 нм. Чтобы прекратить эмиссию электронов, нужно приложить между катодом и анодом задерживающую разность потенциалов 1,7 В. Определить работу выхода для лития.

614. Кванты света с энергией 4,9 эВ вырывают электроны из металла с работой выхода 4,5 эВ. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона.

615. При фотоэффекте с платиновой поверхности величина задерживающего потенциала оказалась равной 0,8 В. Найти длину волны применяемого излучения и максимальную длину волны, при которой еще возможен фотоэффект.

616. Определить поверхностную плотность потока энергии излучения, падающего на зачерненную поверхность, если световое давление на эту поверхность при перпендикулярном падении лучей равно 10 мкПа.

617. Давление монохроматического света с длиной волны 600 нм на черную поверхность, расположенную перпендикулярно падающим лучам, равно 0,1 мкПа. Определить число фотонов, падающих за 1 с на поверхность площадью 1 см?

618. На поверхность площадью 100 см² ежеминутно падает световая энергия 63 Дж. Найти величину светового давления когда поверхность 1) полностью отражает все лучи; 2) полностью поглощает все лучи.

619. Колба электрической лампы представляет собой сферу радиусом 3 см. Часть стенки колбы изнутри посеребрена. Лампа потребляет мощность 60 Вт, 80 % которой затрачивается на излучение. Определить световое давление на посеребренную часть стенки колбы с коэффициентом отражения, равным 0,8.

620. Световой поток мощностью 9 Вт нормально падает на поверхность площадью 10 см², коэффициент отражения которой равен 0,8. Какое давление испытывает при этом данная поверхность?

621. Фотон с энергией 0,15 МэВ испытал рассеяние на покоившемся свободном электроне, в результате чего его длина волны увеличилась на 1,5 пм. Найти угол , под которым вылетел комптоновский электрон отдачи.

622. Рентгеновское излучение с длиной волны 55,8 пм рассеивается плиткой графита (комптон-эффект). Определить длину волны излучения, рассеянного под углом =60^О к направлению падающего пучка.

623. Фотон с энергией 0,4 МэВ рассеялся под углом =30^О на свободном электроне. Определить энергию рассеянного фотона и кинетическую энергию электрона отдачи.

624. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян на угол =180^О.

625. Определить энергию, массу и импульс фотона с длиной волны 1,6 пм.

626. С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 520 нм?

627. Найти массу фoтона, импульс которого равен импульс равен импульсу молекулы водорода при температуре 20 С. Скорость молекулы считать равной средней квадратичной скорости.

628. К электродам рентгеновской трубки приложена разность потенциалов 60 кВ. Наименьшая длина волны рентгеновских лучей, получаемых от этой трубки, равна 19,4 пм. Найти из этих данных постоянную Планка.

629. Найти коротковолновую границу непрерывного рентгеновского спектра, если известно, что уменьшение приложенного к рентгеновской трубке напряжения на 23 кВ увеличивает искомую длину волны в два раза.

630. Какую разность потенциалов надо приложить к рентгеновской трубке, чтобы получить рентгеновские лучи с длиной волны 1,6 пм.

631. Определить частоту обращения электрона на второй орбите атома водорода.

632. Определить потенциал ионизации атома водорода.

633. Определить первый потенциал возбуждения атома водорода.

634.Определить длину волны, соответствующую третьей спектральной линии в серии Бальмера.

635. Вычислить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.

636. Найти период обращения электрона на третьей орбите в атоме водорода.

637.Сколько спектральных линий и в каких сериях будет испускать атом водорода, который возбуждают до 6-го энергетического состояния?

638.Найти радиус первой боровской орбиты электрона для однократно ионизированного гелия и скорость электрона на ней.

639.Найти первый потенциал возбуждения однократно ионизированного гелия.

640. Определить наибольшую и наименьшую длины волн в первой инфракрасной серии спектра водорода (серии Пашена).

641. Определить длину волны де Бройля _Б для электрона, находящегося в атоме водорода на третьей боровской орбите.

642. Определить длину волны де Бройля _Б для нейтрона, движущегося со средней квадратичной скоростью при Т=290 К.

643.Протон движется в однородном магнитном поле с индукцией В=15 мТл по окружности радиусом R=1,4 м. Определить длину волны де Бройля _Б для протона.

644. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля _Б для него была равна 1 нм.

645. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны де Бройля.

646. Электронный пучок выходит из электронной пушки пoд воздействием разности потенциалов U=200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10 %.

647. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10 % от его числового значения, определить неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории?

648. Воспользовавшись соотношением неопределенности, оценить размытость энергетического уровня Е в атоме водорода в электрон-вольтах: 1) для основного состояния; 2)для возбужденного состояния (время его жизни t = 10^-8 с.);

649. Длина волны  излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния t = 10^-8 с, определить отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом Е/Е.

650. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить (в электрон-вольтах) неопределенность энергии этого электрона.

651. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n=2). Определить вероятность обнаружения частицы в области 3/8 l5/8 l.

652. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками». Определить вероятность нахождения электрона в средней трети «ямы»,если электрон находится в возбужденном состоянии (n=3).

653. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы».

654. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками» находится в возбужденном состоянии (n=3). Определить, в каких точках «ямы» (0  l) плотность вероятности обнаружения частицы максимальна. Пояснить полученный результат графически.

655. Для условия задачи 4 определить, в каких точках «ямы» (0  l) плотность вероятности обнаружения частицы минимальна. Пояснить полученный результат графиком.

656. Электрон с энергией E=4 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высоты U=10 эВ и шириной l = 0,1 нм. Определить коэффициент D прозрачности потенциального барьера.

657. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определить в электрон-вольтах разность энергии U-E, при которой вероятность прохождения электрона сквозь барьер составит 0,5.

658. Протон с энергией E=5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U=10 эВ и шириной l = 0,1 нм. Определить вероятность прохождения протоном этого барьера.

659. Во сколько раз надо сузить ширину барьера в условии задачи 8, чтобы вероятность прохождения барьера протоном стала равна 0,5?

660. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U‑E = 5 эВ. Определить, во сколько раз изменится коэффициент прозрачности барьера D для электрона, если разность U-E возрастет в 4 раза.

661. Первоначальная масса радиоактивного изотопа йода (период полураспада Т_1/2 = 8сут) равна 1 г. Определить: 1)начальную активность изотопа; 2)его активность через 3 сут.

662. Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить его активность по истечении промежутка времени, равного половине периода полураспада.

663. Начальная активность 1г изотопа радия равна 1 Ки. Определить период полураспада Т_1/2 этого изотопа.

664. Определить период полураспада Т_1/2 некоторого радиоактивного изотопа, если его активность за 5сут уменьшилась в 2,2 раза.

665. Определить удельную активность p (число распадов в 1 с на 1 кг вещества) изотопа , если период его полураспада Т_1/2=4,510⁹ лет.

666. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается после трех - и двух ^--распадов.

667. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается после шести- и трех ^--распадов.

668. Определить, сколько - и -частиц выбрасывается при превращении ядра таллия в ядро свинца .

669. Радиоактивный изотоп радия претерпевает четыре -распада и два ^--распада. Определить для конечного ядра: 1) зарядовое число Z; 2) массовое число А.

670. Какой изотоп образуется из после четырех -распадов и двух -распадов.

671. Определить энергетический эффект реакции .

672. Определить энергетический эффект реакции .

673. Определить зарядовое число Z и массовое число А частицы, обозначенной буквой , в символической записи ядерной реакции:

674. Записать недостающие обозначения  в следующих реакциях:

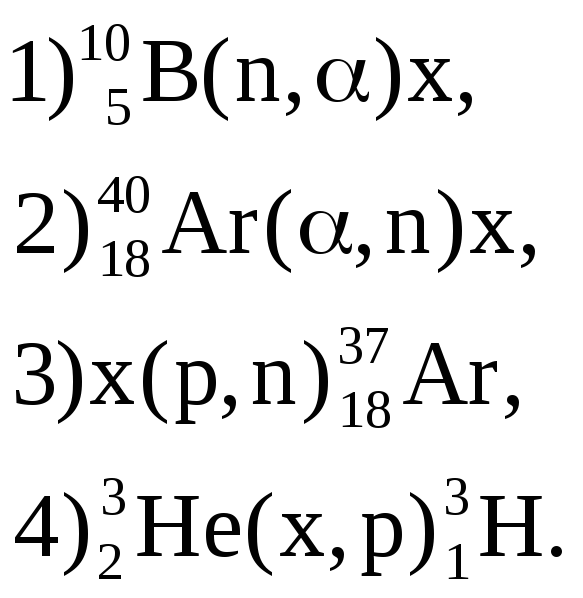
675. Дополнить недостающие обозначения  в следующих ядерных реакциях:

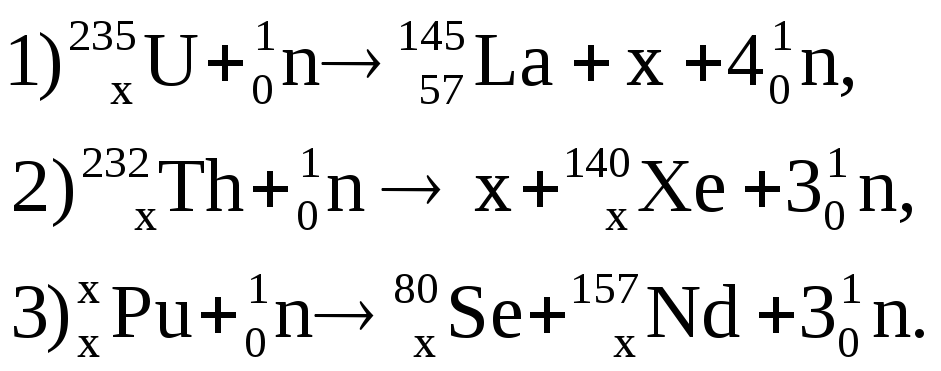
676. Определить число нейтронов, возникающих за 1 с. в ядерном реакторе тепловой мощностью Р = 200 МВт,если известно, что при одном акте деления выделяется энергия Е = 200 МэВ, а среднее число нейтронов на один акт деления составляет 2,5.

677. Какое количество воды можно нагреть от 0 C до кипения, если использовать все тепло, выделяющееся при реакции ,при полном разложении 1 г лития? С_в=4,1910 ³ Дж/(кгК).

678. Какое количество энергии в киловатт-часах можно получить от деления 1 г. урана , если при каждом делении выделяется энергия, приблизительно равная 200 МэВ.?

679. Какое количество урана расходуется в сутки на атомной электростанции мощностью 510³ кВт? КПД принять равным 17 %. Считать, что при каждом акте распада выделяется энергия 200 МэВ.

680. При взрыве водородной бомбы протекает термоядерная реакция образования гелия из дейтерия и трития. Написать эту реакцию, найти ее энергетический эффект. Какое количество энергии можно получить при образовании 1 г гелия?

Варианты контрольных заданий.

Номер варианта	Номера задач.
1	601	611	621	631	641	651	661	671
2	602	612	622	632	642	652	662	672
3	603	613	623	633	643	653	663	673
4	604	614	624	634	644	654	664	674
5	605	615	625	635	645	655	665	675
6	606	616	626	636	646	656	666	676
7	607	617	627	637	647	657	667	677
8	608	618	628	638	648	658	668	678
9	609	619	629	639	649	659	669	679
10	610	620	630	640	650	660	670	680