1.4. Обработка и анализ результатов испытаний

При проведении испытаний необходимо очень тщательно, акку­ратно и без ошибок записывать в лабораторной работе все пер­вичные результаты измерений. Отбрасывание при этом резко отличающихся (выскакивающих) результатов допускается лишь после соответствующего анализа (см. с. 18). При записи такие результаты обводят цветным карандашом. Первичные резуль­таты и подсчитываемые затем сводные характеристики записы­вают с учетом погрешности приборов и измерений.

Числовые результаты, получающиеся в процессе исследова­ния свойств текстильных материалов, обычно неодинаковы, и по ним трудно оценить исследуемое свойство, особенно при боль­шом числе испытаний. Поэтому проводят уплотнение информа­ции, заменяя многочисленные первичные результаты сводными характеристиками среднего уровня исследуемого свойства и его неравномерности.

Однако выборочные сводные характеристики, полученные при испытании небольшой выборки, а не всего исследуемого ма­териала, нельзя распространять на весь материал (генеральную совокупность). Сводные характеристики для всего материала могут отличаться от выборочных в пределах доверительных гра­ниц, которые определяют с заданной доверительной вероятно­стью, зависящей также от закона распределения первичных ре­зультатов [1.8].

ЗАПИСЬ РЕЗУЛЬТАТОВ ИСПЫТАНИИ

Запись первичных данных. Низший разряд * записываемых ре­зультатов должен соответствовать низшему разряду цены деления шкалы прибора, т. е. значению одного наименьшего деления шкалы, выраженного в единицах измерения.

* Термин «низший разряд» относится не только к целым числам, но и к цифрам после запятой.

Если при испытании получится результат, резко отличаю­щийся от остальных, его обязательно записывают и выделяют, чтобы затем проверить анормальность этого результата и оста­вить или отбросить его как выскакивающий.

Первичные результаты являются приближенными числами, и в них необходимо различать верные и неверные, значащие и незначащие цифры.

Верными называют цифры тех разрядов, которых нет в ошибке выборки или в абсолютной погрешности приближенного числа, а также цифры разрядов, записанных в ошибке нулями слева. Остальные цифры будут неверными. Например, в ре­зультатах 1,973 ± 0,004, 1002 ± 5 и 0,068 ± 0,001 по три верные цифры и по одной неверной, а в приближенном числе 15,48 ± ± 0,32 две верные и две неверные цифры. Неверную цифру выс­шего разряда иногда называют сомнительной.

Значащими называют все цифры, кроме нулей, записан­ных подряд слева. Нули, записанные подряд справа, могут быть значащими или незначащими. Последними считают нули, записанные в погрешности подряд справа. Например, в резуль­тате 2900 + 10 незначащим является один последний нуль справа.

В первичных результатах число неверных цифр равно числу разрядов (начиная с наивысшего значащего) абсолютной по­грешности измерений или цены одного деления шкалы прибора.

Запись промежуточных и итоговых результатов. В промежу­точных результатах, используемых в последующих вычислениях, отбрасывают все лишние цифры и оставляют после округления две неверные цифры. Вторую неверную цифру отбрасывают уже в окончательном результате. Таким образом, итоговый резуль­тат должен иметь все верные цифры, за исключением одной по­следней (сомнительной) в низшем разряде. Если окончательный результат приводят вместе с абсолютной погрешностью или ошибкой выборки, то их также округляют до разряда последней оставленной цифры итогового результата. Например, 12,47 ± ± 0,63 « 12,5 ± 0,6; 1028 ± 17 « 1030 ± 20.

Правила округления. Когда отбрасываемая при округлении цифра меньше 5, цифру в сохраняемом смежном разряде не из­меняют. Если отбрасываемая цифра больше 5, сохраняемую цифру увеличивают на единицу. Наконец, когда отбрасываемая цифра равна 5, сохраняемую цифру либо увеличивают на еди­ницу, если она нечетная, либо не изменяют, если она четная или нуль. В том случае, когда вместе с цифрой 5 отбрасывают и другие цифры (помимо нулей), сохраняемую цифру увеличивают на единицу. Если же отбрасываемая цифра 5 получилась в ре­зультате округления с дополнением, сохраняемую цифру не из-м.'пиют. Например, 84,6512 да 84,7; 2,346 » 2,35 « 2,3.

Предельная ошибка одного округления равна 0,5 единицы сохраняемого разряда. Ее величина не должна быть больше суммарной ошибки измерения.

ОПРЕДЕЛЕНИЕ СВОДНЫХ ВЫБОРОЧНЫХ ХАРАКТЕРИСТИК ПРИ МАЛОМ ЧИСЛЕ ИЗМЕРЕНИЯ (п < 50)

Выборочное среднее определяют по формуле

(1.5)

где n — число измерений (объем выборки); x_i — отдельные результаты изме­рений.

Если х используют для других расчетов, его обычно записы­вают на один разряд ниже низшего разряда в отдельных изме­рениях. Если х характеризует итоговый результат испытаний, его округляют до низшего разряда первичных данных.

Среднее квадратическое отклонение может быть смещенным (S) и несмещенным ( ). Усредненные смещен­ные значения S в малых выборках занижены по сравнению со средним квадратическим отклонением а для всей партии ма­териала.

При неизвестной средней величине а для всей партии мате­риала S подсчитывают по формуле

(1.6)

а — по формуле

(1.7)

где Мk — коэффициент, значения которого приведены в табл. 1.2 (k = n-1, если а неизвестно, и k = n, если а известно; п — число измерений).

Таблица 1.2

и	Mk k		Mk k		Mk k		Mk
1	1,253	6	1,042	14	1,018	30	1,008
2	1,128	7	1,036	15	1,017	35	1,007
3	1,085	8	1,032	19	1,013	40	1,006
4	1,064	9	1,028	20	1,013	50	1,005
5	1,051	10	1,025	25	1,010	60	1,004

Примечание. При n>60 М_k, = 1.

Усредненные для многих выборок значения S соответствуют ориентировочно σ. Определенная по формуле (1.6) выборочная дисперсия S² является несмещенной оценкой и в среднем соот­ветствует по уровню дисперсии σ² для всей партии материала

Коэффициенты вариации также могут быть смещен­ными (С) и несмещенными ( ). Их определяют в процентах по следующим формулам:

С =1005/ ; (1.8)

=100 / . (1.9)

Размах варьирования R. определяют для т выборок по n ≤ 10 в каждой:

R=x_max̶ x_min (1.10)

Неравномерность материала оценивают по среднему раз­маху

(1.11)

где R_t — значение размаха в i-й выборке.

Несмещенная оценка S_R среднего квадратического отклоне­ния σ для всей партии материала определяется также по сред­нему размаху

(1.12)

где а_п — коэффициенты, определяемые в зависимости от объема выборки по ГОСТ 11.004—74 (СТ СЭВ 876—78)[1.91:

n	2	3	4	5	6	7	8	9	10
an	0.8862	0.5908	0.4857	0.4299	0.3946	0.3698	0.3512	0.3312	0.3367

Выборку большого объема следует разделить случайным ме­тодом на т равных групп (объемом л каждая) и по формулам (1.10) — -(1.12) определить/?, К и 5#. Например, для выборочных данных табл. 1.3, которая приведена ниже, #=(14 + 41 + ... ... +25 + 43) /10 = 27,2 сН, а 5_Д = 0,3249-27,2 = 8,84 сН

.

ОПРЕДЕЛЕНИЕ СВОДНЫХ ВЫБОРОЧНЫХ ХАРАКТЕРИСТИК ОДНОСТУПЕНЧАТОЙ ВЫБОРКИ ПРИ БОЛЬШОМ ЧИСЛЕ ИЗМЕРЕНИИ

При дробных значениях измеряемых величин XI и х, а также большом числе испытаний вычисление сводных характеристик, особенно 5 и 5², затруднительно и трудоемко. Поэтому в данном случае применяют предварительную группировку первичных данных по классам и определяют отклонения не от выборочного среднего х, а от условного центра хо-

Рассмотрим на примере обработку методом произведений результатов 100 измерений разрывной нагрузки нити в санти-ньютонах (табл. 1.3).

Прежде всего в табл. 1.3 находят максимальное и минималь­ное значения (х_тах = 139, х_т1п = 92) . Затем все результаты рас­пределяют в табл. 1.4 по п_к классам с одинаковым интервалом k

Таблица 1.3

Первичные результаты										Размах
112	104	109	113	ПО	108	113	111	102	99	14
127	ПО	102	109	105	95	136	129	ПО	126	41
111	123	120	101	111	115	109	112	120	119	22
112	108	115	98	112	107	111	112	101	120	22
118	104	116	114	96	121	116	114	108	95	26
109	115	98	111	113	103	110	111	117	97	20
101	99	112	111	108	113	114	112	121	95	26
112	105	112	125	111	116	106	115	103	92	33
105	105	98	105	123	121	104	101	111	98	25
120	112	120	109	139	109	96	113	112	98	43

Число классов зависит от объема выборки: 7 ≤ n_к ≤ 20. Классовый интервал k, или разницу между нижними (верхними) пределами смежных классов, определяют по формуле k = (х_тах — Х_тiп)/п_к. Желательно, чтобы величина k была крат­ной 5 или 10, так как тогда облегчается разноска первичных данных из табл. 1.3 в расчетную табл. 1.4. Для данных табл. 1.3 при п_к = 10 классовый интервал k = (139— 92)/10 —4,7. Вели­чину k округляем, т. е. принимаем кратной 5 (и = 5).

Таблица 1.4

Границы классов	Отметки числа результатов В границах классов	Часто­та и	... ОС	ЦОС	их.
1	2	3	4	5	6
135-139	//	?	+5	10	50
130- 134		0	+4	0	0
125-129	////	4	+ 3	12	36
120 -124	//// ////	10	+ 2	20	№
115- 119	//// ////	10	+ 1	10	10
110-114	//// //// //// //// //// //// //	32	0	0	0
105-109	//// //// //// //	/7	-/	-п	17
100 -104	//// //// /	11	-2	-22	№
95-99	//// //// ///	/4 -	-3	-39	1П
90- 94	/	/	-4	-4	16
		100		-30	330

В верхней строке графы 1 табл. 1.4 слева записывают наи­больший результат х_тах, округленный в меньшую сторону с точ­ностью k (х_тах = 139 ≈ 135). Каждое число, записываемое сле­ва в следующих строках графы 1, определяют последовательным вычитанием интервала k. до получения минимального результата из табл. 1.3 (х_тin = 92) или числа, меньшего его. Таким образом находят все нижние границы классов. Верхние границы классов определяют, прибавляя к нижним границам интервал и и вы­читая величину низшего разряда г первичных результатов. Для нашего примера /г = 5 и г= 1; поэтому верхние границы клас­сов больше нижних на и — г = 4. Верхние границы записывают в графе 1 справа, отделяя их от нижних чертой.

В графе 2 черточками отмечают подряд каждый результат из табл. 1.3 в строке того класса, в границах которого он нахо­дится. Первые четыре результата удобно отмечать наклонными или вертикальными черточками, а пятый — соединяющей их го­ризонтальной чертой. По сумме отметок определяют частоту и, которую фиксируют в графе 3.

Условный центр х₀ намечают примерно против одной из наи­больших частот или в интервале, где ожидается среднее значе­ние. Центру соответствует условное отклонение а — 0, фикси­руемое в графе 4. В ней же записывают для каждой строки по­следовательно изменяющиеся на единицу отклонения ее: вверх от нуля — положительные, вниз — отрицательные. Затем для всех классов вычисляют произведения иа и иа², которые запи­сывают соответственно в графах 5 и 6. Далее подсчитывают суммы ∑иα, ∑иα² и условные моменты т_i = ∑αu/n, т₂ =∑иα²/n

Определив значение х₀ как среднее границ класса с а = О, вычисляют выборочное среднее х, среднее квадратическое откло­нение 5 и коэффициент вариации С [последний по формуле (1.8)]:

(1.13)

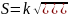(1.14)

где & — классовый интервал; п = Ей — общее число измерений.

Пример 1.3. Для данных табл. 1.4 получаем: /г = 135 — 130 = 5' _Хо = 0,5(110+ 114)_ = 112;_ш, == —30/100 = —0,3; т_г = 330/100 = 3,3. Тре­буется определить х, 5, К,, 5_К, С.

Пользуясь формулами (1.8), (1.11) — (1,14), высчитываем: л: = 112— 5 • 0,3= = 110,5 сН; 5 = 5 д/(3,3 — 0,3²) 100Д100 — 1) = 9 сН; С = 100 • 9/110,5 = 8,1%; К = (14 + 41 +... + 43)/10 = 27,2 сН; Зк = 0,3249-27,2 = 8,83 сН; С =• = 100-8,83/110,5 = 8%.

ПРОВЕРКА СООТВЕТСТВИЯ ОПЫТНОГО РАСПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОМУ

Для выборок объемом 3 ≤ n ≤ 50 по ГОСТ 11.006—74 (СТ СЭВ 1190 — 78) [1.0] допускается применять критерий W с целью проверки согласия опытного распределения с нормальным или логарифмически нормальным распределением.

Результаты измерений ранжируют в порядке их возрастания: х₁≤х₂ ≤ ... ≤x_i≤ …х_п. Далее в графу 1 табл. 1.5 -записывают значения порядкового индекса i=1, 2, . . . , n, а в графу 2 — соответствующие ранжированные значения х,

Таблица 1.5

1	Х1	i
1	2	3 4	5	6		7
1	30	900
2	34	1156
3	41	1681
4	46	2116
5	47	2209
6	47	2209 5 0,0399			47-47=0	0
7	48	2304 4 0,1224			48—46=2	0,2448
8	49	2401 3 0,2141			49— 41=8	1,7128
9	52	2704 2 0,3291			52-34=18	5,9238
10	58	3364	0,5739		58—30=28	16,0692

452 21044 23,9506

(в табл. 1.5 для примера приведены ранжированные результаты п = 10 измерений линейной плотности нити).

В графу 3 записывают значения x², а в графу 4 значения порядкового индекса i=1,2, ..., е, начиная с последней строки и в обратном порядке по сравнению с записью значений ин­декса г. При этом е = 0,5n, если п четное число, и е = 0,5 (n— 1), если я нечетное число.

В графу 5 записывают соответствующие индексу i значения коэффициента а_л-i+1 которые определяют для данного числа из­мерений я и каждого индекса i≤ е по табл. 1.6.

В графу 6 табл. 1.5 записывают вычисленные разности x_n-i+1 —x_i, начиная со строки j = е (или i = п — j + 1) и ниже. Например, для последней строки j= 1 определяют по табл. 1.5 x_10-1+1—xj =x₁₀— х_i = 58 — 30 = 28. В графу 7 записывают значения произведений а_n-j+1(x_n-j+1-x_j), т.е. произведение личин граф 5 и 6. Данные граф 2, 3 и 7 суммируют и записывают в последней строке таблицы.

Затем вычисляют значения φ² и b²:

(1.15)

(1.16)

Критерий согласия определяют по формуле

W= (1.17)

и сравнивают с табличным значением зависимости от объема выборки:

n	3	4	5	10	20	25	30	40	50
W0.05	0.767	0.748	0.762	0.845	0.905	0.918	0.927	0.940	0.947

а верхнюю — по формуле

а_в1 = x⁻ + t₁S/ , (1.19)

где t_i — квантиль распределения Стьюдента при доверительной вероятности уi = 0,95, определяемый по табл. 1.7.

Т а б л и ц а 1.7

															zв
				zн		zв						zн
k=n-1		t1	t					ti		t
							k=n-1	ДЛЯ
		yi =0,95	у=0,95	для у!=0,95				γ=0.95		у=0,95		для γ1=0,95
2	2,920		4,303		0,578	4,42	29		1,699		2,045		0,825	1,28
3	2,353		3,182		0,620	2,92	40		1,684		2,021		0,847	1,23
4	2,132		2,776		0,649	2,37	50		1,676		2,009		0,861	1,20
9	1,833		2,262		0,729	1,65	100		1,660		1,984		0,897	1,13
19	1,729		2,093		0,794	1,37	со		1,645		1,960		1,000	1,00

Примечание. Для промежуточных значений k=n— 1 квантили t определяют линейным интерполированием.

Вероятность нахождения генеральной средней а в пределах односторонних доверительных границ (а_н1; ) и (— ;а_в1) определяется по формулам

P(a≥a_н1) = γ; (1.20)

P(a≤a_в1) = γ. (1-21)

Если в формулы (1.18) и (1.19) подставить из табл. 1.7 вместо ^ значение I, то в формулах (1.20) и (1.21) доверитель­ная вероятность γ₁ = 0,5 (1 + γ) = 0,5 (1 + 0,95) = 0,975.

Нижнюю и верхнюю границы двустороннего доверительного интервала а_Н2 и а_в2 находят по формулам

(1.22)

(1.23)

_где t — квантиль распределения при доверительной вероятности γ = 0,95, оп­ределяемый по табл. 1.7; — величина, называемая также ошибкой вы­борки среднего.

Вероятность нахождения генеральной средней в пределах двусторонних границ определяется по формуле

Р(а_н2≤а≤а_в2) = γ (1.24)

Если в формулы (1.22) и (1.23) подставить из табл. 1.7 вме­сто t значения t₁, то в формуле (1.24) доверительная вероят­ность γ = 2γ₁ — 1 = 2 • 0,095 — 1 = 0,90.

Доверительные границы среднего квадратического отклонения σ. Если генеральная средняя а неизвестна, то, вычислив по фор­муле (1.6) или (1.14) выборочную характеристику 5, задаются доверительной вероятностью у\ и по табл. 1.7 находят при п ≤ 100 значения г_н и z_в. Их значения для промежуточных зна­чений & определяют линейным интерполированием. При k = п — 1 > 100 значения г_л и г_в вычисляют по формулам

; (1.25)

, (1.26)

где и_γ = t при n = берут по табл. 1.7.

Нижнюю одностороннюю доверительную границу находят по формуле

σ_н1 =z_н S (1-27)

а верхнюю одностороннюю доверительную границу — по формуле

σ_в1 =z_в S (1.28)

По аналогии с формулами (1.20), (1.21) и (1.24) имеем сле­дующие вероятностные определения доверительных границ:

Р(σ≥σ_н1) = γ1; (1-29)

Р(σ≤σ_в1) = γ1 (1-30)

Р(σ≤σ≤ σ_в2) = γ. (1-31)

Значения двусторонних доверительных границ σ_Н2 и σ_в2 опре­деляют по формулам (1.27) и (1.28), беря значения г_н и z_К при γ1 = 0,975. В этом случае в формуле (1.31) доверительная ве­роятность γ = 2γ1 — 1=2*0,975 — 1 = 0,95. Значениям г_н и z_В из табл. 1.7 при γ1 = 0,95 соответствует двусторонняя довери­тельная вероятность γ = 0,90.

Доверительные границы коэффициента вариации. Односторон­ние доверительные границы коэффициента вариации V для генеральной совокупности приближенно определяют при п ≥30 и С < 25 % по РС 2049 — 69, используя следующие формулы:

V_Н1 = КнС; (1.32)

_VВ1 = К_ВС, (1.33)

где С — выборочный коэффициент вариации, определяемый по формуле (1.8); значения /(„ и Кв для односторонней доверительной вероятности -vi = 0,95 определяют в зависимости от объема выборки (табл. 1.8).

Таблица 1.8

п	•30	50	100	200	300	500	1000
кв	1,27	1,20	1,13	1,10	1,07	1,06	1,04
/с„	0,83	0,86	0,90	0,92	0,94	0,95	0,97

По аналогии с формулами (1.29) — (1.31) имеем

Р(V≥V н1) = γ₁. (1.34)

Р(V≥V н1) = γ₁. (1.34)

Доверительный интервал с двусторонней вероятностью у = 2у1 — 1=2- 0,95 — 1 = 0,90 можно определить по формуле

P(Vн1≤V≤V_в1) = γ. (1.36)

Пример 1.4. По данным табл. 1.4 в примере 1.3 были подсчитаны выбо­рочные характеристики: х = 110,5 сН, 5 = 9 сН и С = 8,1 %. Необходимо определить односторонние границы генеральных характеристик а, а и V с ве­роятностью vi = 0,95.

При п = 100 и у, = 0,95 по табл. 1.7 находим /, = 1,66 и г„ = 1,13 а по табл. 1.8 — Кв = 1,13. Затем по формулам (1.18), (1.28) и (1.33) опреде­ляем:

я_Н| = 1Ю,5 -1,66 -9/100= 109 сН; Р (а > 109) = 0,95; о-_В1 = 1,13 • 9 = 10,2 сН; Р (а < 10,2) = 0,95; У_В1 = 1,13 - 8,1 = 9,2%; Р (V < 9,2) = 0,95.

Список литературы

1.1 ГОСТ 12.4.113—82. Работы учебные лабораторные. Общие требования безопасности.

1.2. ГОСТ 10681—75* (СТ СЭВ 2038—79). Материалы текстильные. Кли­матические условия для кондиционирования и испытаний проб и методы их определения.

1.3. ГОСТ 8844—75*. Полотна трикотажные. Правила приемки и метод отбора образцов.

1.4. ГОСТ 9173—76. Изделия трикотажные. Правила приемки и методы отбора образцов.

1.5. Лабораторный практикум по материаловедению швейного производ­ства. М., 1979.

1.6. Лабораторный практикум по текстильному материаловеденюо/Ку-кин Г. Н., Соловьев А. Н. и др. М., 1974.

1.7. Методы определения свойств хлопка-волокна/Иванов С. С., Ладыни­на Л. П., Соловьев А. Н. и др. М., 1972.

1.8. А. Н. Соловьев, С. М. Кирюхин. Оценка и прогнозирование качества текстильных материалов. М., 1984.

1.9. ГОСТ 11.004-74 (СТ СЭВ 876—78). Прикладная статистика. Правила определения оценок и доверительных границ для параметров нормального рас­пределения.

1.10. ГОСТ 11.006—74 (СТ СЭВ 1190—78). Прикладная статистика. Пра­вила проверки согласия опытного распределения с теоретическим.

1.11. ГОСТ 11.002—73 (СТ СЭВ 545—77). Прикладная статистика. Пра­вила оценки анормальности результатов наблюдений.

1.12. Венецкий К. Г., Венецкая В. И. Основные математико-статистические понятия и формулы в экономическом анализе. М., 1974.