8

Лабораторные работы №8

«ПОЛЯРИЗАЦИЯ СВЕТА

ПРОВЕРКА ЗАКОНА МАЛЮСА»

Цель работы: Изучение способов получения поляризованного света. Проверка закона Малюса.

Приборы и материалы: источник света, поляроиды, мультиметр, пластинки слюды.

Поляризованный и естественный свет.

Световые волны поперечны: электрический вектор и магнитный вектор волны взаимно перпендикулярны и лежат в плоскости, перпендику­лярной направлению распространения волны - вектору скорости волны V.

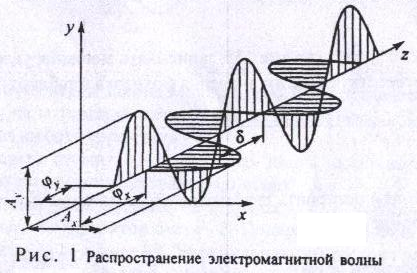
На рис.1 представлена моментальная фотография плоской монохроматиче­ской волны, распространяющейся в направлении оси X. Поля и волны лежат в двух взаимно перпендикулярных плоскостях. Такая волна называется плоско или линейно поляризованной. Векторы и в каждой точке простран­ства ориентированы вдоль одной линии. В общем случае поле плоской монохро­матической волны представляет собой сумму двух взаимно перпендикулярных по­лей, соответствующих двум линейно поляризованным волнам с разностью фаз π/2 . Такая волна называется эллиптически поляризованной, её поле может быть за­писано в виде:

Е _у= Е₀₁ cosω(t-х/V); Е_Z= ±Е₀₁ sinω(t-х/V);

Н_Z=Н₀₁ cos ω(t-х/V); Н_у=±Н₀₁ sinω(t-х/V); ⁽¹⁾

Световое действие связано лишь с электрическим полем волны, поэтому будем в дальнейшем рассматривать лишь вектор (световой вектор). Из (1) следует, что в эллиптически поляризованной волне конец вектора в каждой точке пространства описывает с течением времени эллипс, полуоси которого равны E₀₁ и E_02. Вращение этого вектора происходит либо по часовой стрелке, либо против нее, если смотреть вдоль оси X чему соответствуют знаки + или - в выражении для Е. В первом случае говорят о правополяризованной, а во втором - о левополяризованной волне. В частном случае, когда E₀₁=E₀₂ и эл­липс вырождается в окружность, говорят о круговой поляризации волны. По­скольку волна распространяется вдоль оси X концы векторов и описывают в пространстве в общем случае спирали с шагом, равным длине волны .

Уравнение (1) соответствует бесконечно длящемуся волновому процессу. Реальные волновые процессы всегда конечны во времени и пространстве, поэтому реальные световые волны – немонохроматичны, а следовательно не поляризованы. Обычные источники света являются совокупностью быстро высвечивающихся (в течение времени ) элементарных источников (атомов или молекул), испускающих свет независимо друг от друга, с разными фазами и с разными ориентациями векторов и . Возникающее электромагнитное излучение называется естественным светом. В нём все направления поля в плоскости, перпендикулярной к , представлены с одинаковой вероятностью. Поэтому естественный свет обладает (статистически) осевой симметрией относительно направления его распространения. Для линейно поляризованного света и для так называемого частично-поляризованного света (суммы естественного и линейно поляризованного) симметрии этой нет.

Для получения, из естественного света линейно поляризованного применяются специальные оптические приспособления – поляризаторы. Направление колебаний электрического вектора в волне, прошедшей через поляризатор, называется разрешенным или главными направлением поляризатора. Ниже приводятся способы получения поляризованного света.

1) Отражение света от диэлектрической пластинки.

Отраженный от диэлектрика свет частично поляризован. Степень поляриза­ции света, отраженного от диэлектрической пластинки в воздух, зависит от по­казателя преломления диэлектрика n и от угла падения i. Полная поляризация отраженного света достигается при падении его под углом Брюстера i_б, который определяется соотношением:

tg i_б =n (1)

где n -относительный показатель преломления диэлектрика относительно воздуха.

В этом случае плоскость колебаний электрического вектора в отраженном свете перпендикулярна плоскости падения.

2) Преломление света в стеклянной пластинке (опыт со стопой Столетова).

Поскольку отраженный от диэлектрической пластинки свет оказывается частично (или даже полностью) поляризованным, проходящий свет всегда по­ляризован частично. Максимальная поляризация проходящего света достигает­ся при падении под углом Брюстера. К примеру, свет падает на стекло с n =1,5. Тогда угол Брюстера i_б = 57°. При таком угле падения отражается при­мерно седьмая часть света, а шесть седьмых преломляется, и проходит в стекло.

Отраженный свет поляризован полностью.

В проходящем же свете поляризована только примерно седьмая часть па­дающего (с колебаниями в плоскости падения), а пять седьмых не поляризова­но. Если свет пропускать последовательно через несколько пластинок (стопа Столетова), то можно добиться почти полной поляризации и в проходящем све­те (с колебаниями светового вектора в плоскости падения).

3) Преломление света в двоякопреломляющих кристаллах (исландский шпат).

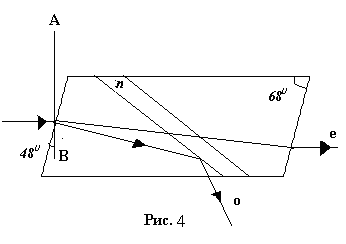
Некоторые кристаллы, например исландский шпат, обладают свойством двойного лучепреломления. Преломляясь в таком кристалле, световой луч раз­деляется на два луча со взаимно перпендикулярными плоскостями колебаний. Двойное лучепреломление не наблюдается лишь в том случае, когда свет в кри­сталле распространяется вдоль оптической оси. Исландский шпат - кристалл одноосный; оптическая ось - это любая прямая в кристалле, параллельная пря­мой АВ, проходящей через тупые углы ромбоэдра (рис.2). Плоскость, проходящая через оптическую ось и падающий луч, называется главной плоскостью или главным сечением.

Если луч света падает нормально на естественную грань кристалла, то он все равно разделяется на два луча - обыкновенный о и необыкновенный е, лежащие в главной плоскости. Оба они будут плоскополяризованы. Электрический век­тор луча e лежит в главной плоскости, а для луча о электрический вектор пер­пендикулярен главной плоскости. Показатель преломления обыкновенного лу­ча n₀=1,658 и не зависит от направления в кристалле; для необыкновенного лу­ча n_е, разный в разных направлениях, от n_е = 1,486 в направлении, перпендику­лярном оптической оси, до n_е= n₀ =1,658 вдоль оптической оси. Из перечислен­ных свойств видно, как можно получить плоскополяризованный свет: нужно пропустить свет через кристалл под углом к оптической оси. Тогда получим два пучка плоскополяризованного света.

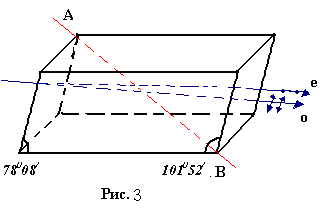
Отклоняя один из лучей в сторону, можно получить плоскополяризованный свет - так устроена, например, поляризацион­ная призма Николя (рис.3).