3 Метрический синтез плоского механизма

На этапе метрического синтеза механизма по заданному техническому заданию и разработанной кинематической схеме определяются геометрические размеры звеньев. Так как для каждого конкретного механизма в зависимости от его назначения методика расчета геометрических размеров звеньев разрабатывается индивидуально ,проиллюстрируем ее на примере метрического синтеза кривошипноползунного механизма (КПН) двухпоршневого насоса двухстороннего действия, входящего в состав машинного агрегата, расчет которого предлагается выполнить в курсовом проекте по курсу ТММ.

Под машинным агрегатом ( Рис 3.1а) понимается устройство, состоящее из машины – двигателя (Д), передаточного механизма – (ПМ), исполнительного механизма (ИМ) и системы регулирования (СР).

Рис. 3.1

Структурная схема машинного агрегата представлена на Рис 3.1б. Исполнительным механизмом в данном случае служит двухпоршневой насос двухстороннего действия, структурная схема которого показана на Рис 3.2.

К ак видно из Рис 3.2 механизм имеет одну степень свободы. Следовательно, для однозначного определения положений всех его звеньев необходимо задать значение одной обобщенной координаты, в качестве которой естественно выбрать угол поворота кривошипа (1).

Исходными данными для расчета являются:

Объемный расход жидкости – Q ;

Число оборотов кривошипа - ;

Диаметр поршня - ;

Отношение длины кривошипа к длине шатуна – . (3.1)

Теоретический расход жидкости будет:

, (3.2)

Где объемный К.П.Д. насоса, учитывающий утечки жидкости. Рис. 3.2

Номинальный рабочий объем одного цилиндра:

(3.3)

Где: - площадь цилиндра,

- рабочий ход поршня .

Для двухпоршневого насоса двухстороннего действия получаем:

(3.4)

Связь между рабочим объемом насоса и его теоретическим расходом будет:

(3.5)

Тогда объем насоса будет:

(3.6)

Рабочий ход поршня определится как :

(3.7)

С другой стороны .

Откуда длина кривошипа будет:

(3.8)

А длина шатуна:

(3.9)

По результатам метрического синтеза вычерчиваем схему механизма в соответствующем масштабе. Масштабный коэффициент определяется :

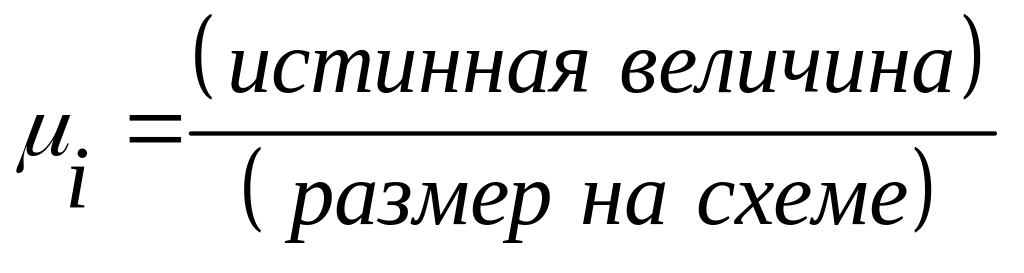(м/мм).

4 Кинематический анализ механизма

На этапе кинематического анализа механизма, как было сказано выше, определяются траектории, скорости и ускорения характерных точек и элементов механизма. При этом силы, действующие на механизм, не учитываются. Кинематический анализ может быть выполнен графическим, графоаналитическим и аналитическим методами.

4.1 Графический метод (метод диаграмм)

Кинематические диаграммы представляют собой графическое изображение функциональных зависимостей перемещения, скорости и ускорения точек или углов поворота, угловых скоростей и ускорений звеньев от заданного параметра (времени или обобщенной координаты).

Диаграмма перемещений строится при определенном положении механизма за один цикл его движения. Диаграммы скорости и ускорений в этом случае строят путем графического дифференцирования диаграммы перемещения. Для построения диаграмм должны быть заданны кинематическая схема механизма, построенная в определенном масштабе, а также скорость ведущего звена.

Графический метод достаточно прост и нагляден, однако вследствие большого объема графических построений обладает большой трудоемкостью малой точностью, поэтому в настоящее время применяется крайне редко.