8.2 Статическая и динамическая балансировка роторов

Ротором называется любое массивное тело, вращающееся вокруг неподвижной оси. Если центр масс ротора не совпадает с осью вращения, то при вращении возникают силы инерции, вращающиеся вместе с ротором и создающие переменные нагрузки на его опорах с частотой вращения ротора. Даже при малых смещениях центра масс эти нагрузки могут достигать значительных величин, особенно у быстроходных роторов. Целью балансировки ротора является частичное или полное устранение инерционных нагрузок на опоры.

8.3 Приведение сил инерции неуравновешенного ротора к каноническому виду

Рассмотрим ротор (Рис 8.4), вращающийся вокруг оси ОА с постоянной угловой скоростью . Центр масс ротора расположен на расстоянии от оси ротора. Выберем элементарную частицу ротора массой расположенной на расстоянии от оси. Центробежная сила инерции, действующая на эту частицу, будет

Рис. 8.4

Приведем все силы инерции к началу координат (О).

Главный вектор сил инерции будет

Учитывая что

Получим

Из теоретической механики известно что

,

Где - масса ротора, а - координаты его центра масс.

Тогда

Т.е. главный вектор сил инерции ротора, приведенный к точке О, перпендикулярен оси Y и лежит в плоскости XOZ.

Момент силы инерции частицы относительно начала координат будет

Где - радиус-вектор определяющий положение частицы.

Представив векторное произведение в виде определителя и раскрывая последний получим

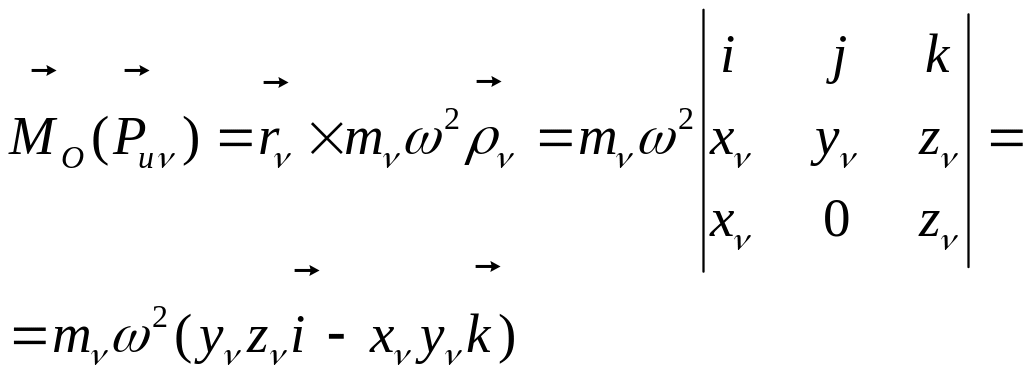
Тогда главный момент сил инерции относительно точки О будет

Выражения, стоящие под знаком суммирования

Называются центробежными моментами инерции. Тогда

Как видно из полученного выражения, главный вектор момента сил инерции расположен в плоскости XOZ и перпендикулярен оси Y. Величина этого вектора равна

Приведем систему к двум скрещивающимся силам. Для этого проведем плоскость Q перпендикулярную (Рис 8.4). В этой плоскости расположим силы и , образующие пару с моментом . Величина этих сил очевидно определится

Где - длина ротора.

Силы и расположены в одной плоскости (II). Равнодействующая этих сил будет

Таким образом, система сил инерции будет эквивалентна системе, состоящей из двух перекрещивающихся сил лежащих в параллельных плоскостях.

При вращении ротора эти силы вращаются в плоскостях I и II перпендикулярной оси вращения с угловой скоростью .

8.4 Балансировка неуравновешенных роторов

Как было показано выше, неуравновешенный ротор действует главный вектор и главный момент сил инерции. Условием уравновешивания вращающегося ротора будет равенство нулю этих составляющих системы инерционных сил.

Для выполнения этих условий необходимо чтобы ось вращения была главной и центральной осью инерции ротора т.е.

Если выполняется условие (центр масс находится на оси вращения), то говорят о статической балансировке.

При и - динамическая балансировка.

Статическая балансировка – превращение оси вращения в центральную ось инерции. Она достигается добавлением или снятием металла ротора до достижения им безразличного статического равновесия. ( ). Эта балансировка применяется для роторов имеющих малую толщину и вращающиеся с незначительной угловой скоростью.

Динамическая балансировка – превращение оси вращения в главную центральную ось инерции. Эта балансировка осуществляется на специальных балансировочных станках или (для больших роторов) на собственной оси путем закрепления на роторе дополнительных масс, расчет величины которых основывается на приведении системы инерционных сил действующих на ротор к двум скрещивающимся силам, действующим в двух произвольно выбранных параллельных плоскостях, как было показано выше. Эти силы можно рассматривать как центробежные силы инерции двух точечных масс и , положение которых в плоскостях I и II определяются радиусами и (Рис 8.5). Величины этих сил будут

Где и - величины дисбалансов, измеряемые на специальных балансировочных станках.

Рис. 8.5

Задача динамической балансировки заключается в подборе масс и располагающихся на известных радиусах и таким образом чтобы

Это условие выполняется при равенстве величин соответствующих дисбалансов

Плоскости I и II (плоскости уравновешивания) определяются в зависимости от конструкции ротора индивидуально.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Артоболевский И.И. Теория механизмов и машин - М.: Наука, 1975г.

2. Теория механизмов и машин, под редакцией К.В. Фролова – М.: ВЫСШАЯ ШКОЛА, 1987г.

3. Махова Н.С. и др. Основы теории механизмов и машин – М.: ВЛАДОС, 2006г.