7.2 Условие статической определимости кинематических цепей

Задачей динамического расчета механизма является определение реакций в кинематических парах и движущий момент (или силу) на ведущем звене. Для решения этой задачи методом кинетостатики необходимо составить систему уравнений, число которых должно быть равно числу неизвестных.

Пусть плоский механизм состоит из звеньев, низших и высших кинематических пар. Число уравнений равновесия, которые можно составить для этого механизма будет - . Каждая низшая кинематическая пара отнимает две степени свободы (т.е. вносит два неизвестных), а высшая одно. Тогда общее число неизвестных будет - . Степень подвижности плоского механизма, как было установлено выше, будет

Для статической определимости механизма необходимо

Для кинематической цепи, у которой (группа Асура)

При - неизвестные силы приложены к ведущему звену.

Таким образом, механизм без избыточных связей статически определим.

7.3 Кинетостатический расчет плоских механизмов с низшими кинематическими парами

Зная активные силы, действующие на механизм, и силы инерции звеньев можно определить силы реакции в его кинематических парах и движущий момент (или силу) на ведущем звене. Эта задача может быть решена аналитическим или графоаналитическим методом.

Механизм расчленяют на структурные группы, которые являются статически определимыми (группы Асура) и проводят последовательный расчет, начиная с наиболее удаленной от ведущего звена группы.

Сила взаимодействия звеньев, образующих низшую кинематическую пару, представляет собой равнодействующую элементарных сил, распределенных по поверхности соприкосновения звеньев (Рис 7.2а, б).

Эта равнодействующая (при отсутствии сил трения) направлена по нормали к поверхности, но ее величина и точка приложения не известны, т.е. каждая низшая кинематическая пара приводит к появлению двух неизвестных, подлежащих определению в процессе расчета. В высших кинематических парах (контакт звеньев происходит либо в точке, либо по линии) сила взаимодействия будет направлена по нормали в точке соприкосновения звеньев (при отсутствии сил трения) (Рис 7.2в). Таким образом, для высшей кинематической пары не известной оказывается только величина силы.

После того как произведен силовой расчет всех структурных групп подвижное звено первичного механизма получает статическую определенность, что дает возможность определить движущую силу, действующую на это звено.

Рис. 7.2

7.4 Кинетостатический расчет двигателя внутреннего сгорания

В качестве примера применения метода кинетостатики проведем расчет двигателя внутреннего сгорания (ДВС), структурная схема которого показана на Рис 7.3.

Как видно из рисунка механизм состоит из трех звеньев: кривошипа (1), шатуна (2) и ползуна (3). Звенья соединяются низшими кинематическими парами: (0-1), (1-2), (2-3) и (3-0). Таким образом, подвижность механизма будет

На механизм действуют:

- внешняя сила давления газов (известна);

- внешний момент полезных сопротивлений (не известен);

- внешние силы веса звеньев (2) и (3) (известны). Считаем, что кривошип (1) сбалансирован противовесом;

- известные силы и моменты сил инерции соответствующих звеньев;

- неизвестные силы и моменты реакций стойки на соответствующие звенья механизма.

Выделим из структурной схемы конечную группу Асура (Рис 7.4а) и обозначим все силы, приложенные к этой группе, заменив действие звена (1) реакцией не известной ни по величине, ни по направлению.

Спроектировав эту реакцию на оси координат (x,y), получим, что неизвестные силы, подлежащие определению, будут: . Число уравнений кинетостатики составленные для этой группы равно трем т.е. задача статически не определенная. Для ее решения воспользуемся известным из теоретической механики приемом,

Рис. 7.3 разделив рассматриваемую группу на два звена (Рис 7.4 б, в) и заменив как и ранее действие отброшенных звеньев соответствующими реакциями ( ). Тогда вводя систему координат (x,y) и составляя уравнения равновесия для каждого звена в отдельности получим.

Для шатуна (Рис 7.4б)

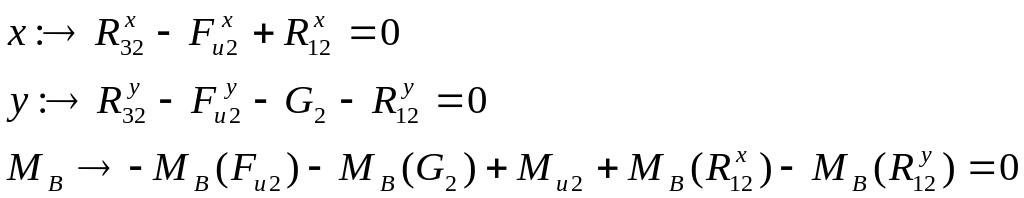
Рис. 7.4

Для ползуна (Рис 7.4в)

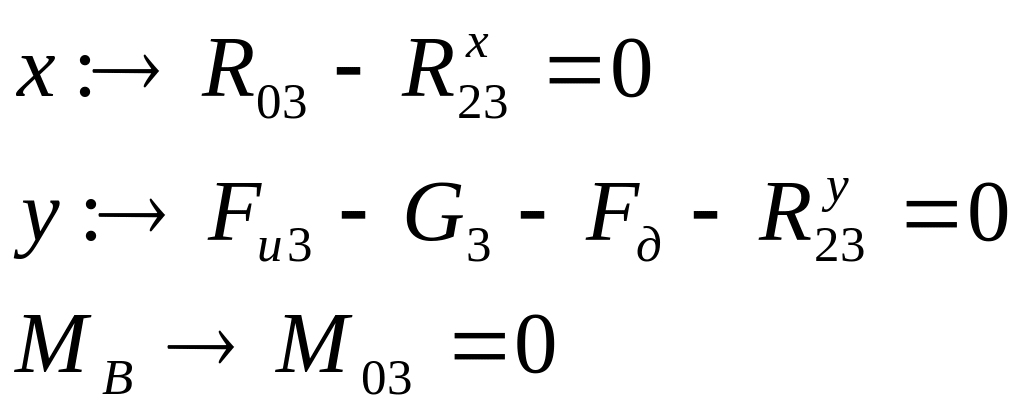
Таким образом, имеем шесть уравнений равновесия, решая которые найдем неизвестные: .

Полная величина реакций в кинематических парах будет

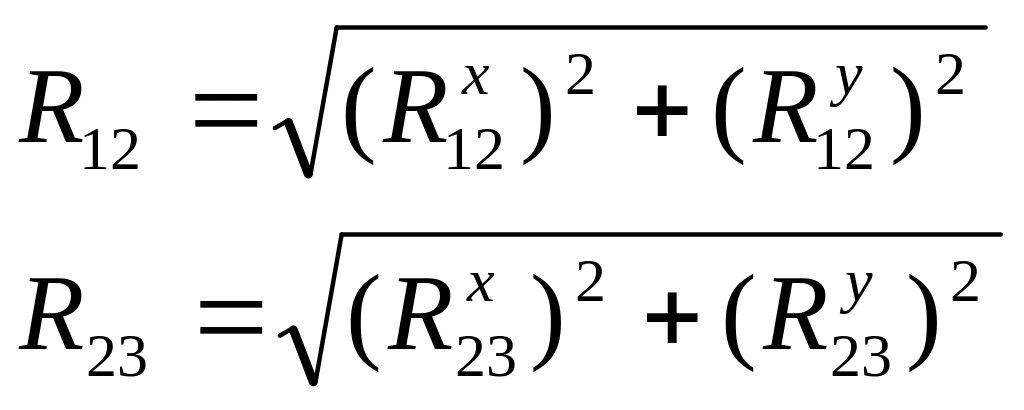
А их направление задается косинусами углов между осью x и соответствующей реакцией

.

Переходя к ведущему звену (Рис 7.4г), обозначим все силы, действующие на него. При этом влияние шатуна заменим его реакцией , известной из предыдущих вычислений. Вводя, как и ранее оси координат запишем уравнения равновесия ведущего звена

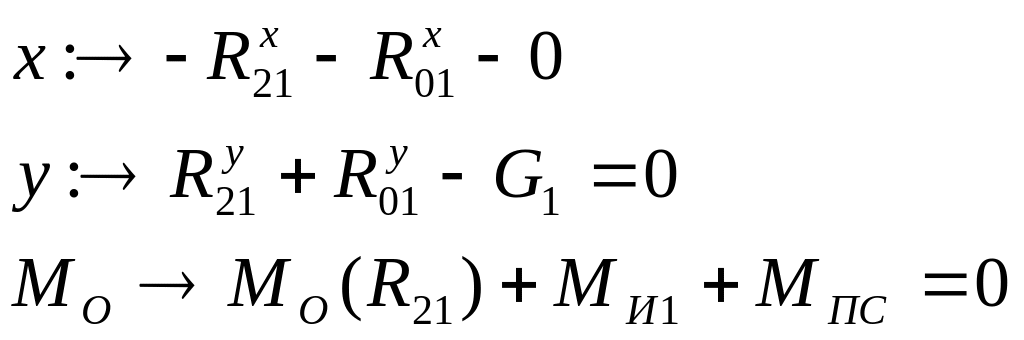
Откуда находим неизвестные:

Полная величина реакции в шарнире (О) будет

А ее направление определиться направляющим косинусом