6.6 Механический коэффициент полезного действия

При работе механизма в установившемся режиме, как следует из выражения (6.11), работа движущих сил идет на преодоление сил полезного и вредного сопротивлений. Для оценки качества механизма с точки зрения использования, поступающей энергии вводится понятие коэффициента полезного действия механизма (КПД) – как отношение абсолютной величины работы (или средней мощности) сил полезного сопротивления к работе (или средней мощности) движущих сил за один полный цикл установившегося движения механизма. Т.е.

(6.16)

Как видно из определения, чем выше КПД, тем более рационально используется поступающая энергия в механизме.

Кроме КПД в практике используется коэффициент потерь, который определяется как отношение величины работы (или средней мощности) сил вредных сопротивлений к работе (или средней мощности) движущих сил. Т.е.

(6.17)

Соотношение между этими коэффициентами очевидно будет

(6.18)

6.7 Кпд сложного механизма

При совместной работе нескольких механизмов в составе машинного агрегата КПД последнего будет определяться как КПД отдельных механизмов, так и способом их соединения. Несколько механизмов в составе сложного могут соединяться последовательно, параллельно или смешанным образом.

Последовательное соединение.

Пусть сложный механизм состоит из последовательно соединенных n механизмов (Рис 6.2а).

Работа источника энергии ( ), приводящая в движение весь механизм, является работой движущих сил для первого механизма.

Работа сил полезного сопротивления для этого механизма ( ) является, в свою очередь, работой движущих сил для второго механизма и т.д. Работой сил полезного сопротивления для всего сложного механизма будет являться работа сил полезного сопротивления последнего звена ( ). Если известны КПД каждого входящего механизма ( ), то по определению КПД получим

Откуда КПД сложного механизма, состоящего из последовательно соединенных между собой n механизмов, будет равна

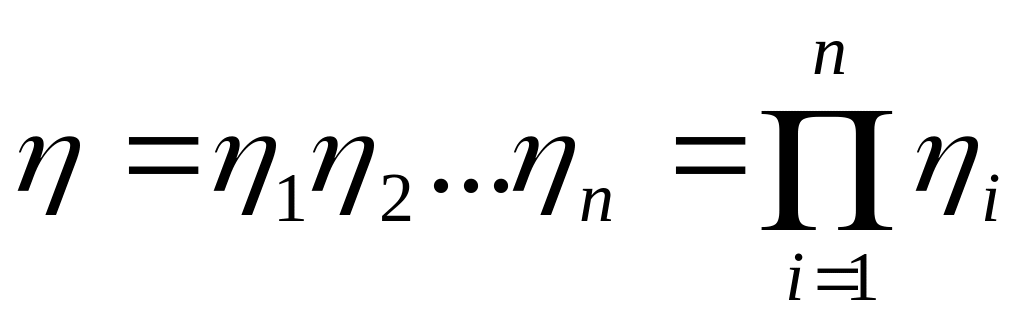(6.19)

Рис. 6.2

При параллельном соединении механизмов в составе сложного как видно из (Рис 6.2б) работа движущих сил источника энергии на входе распределяется между отдельными механизмами, а работа сил полезного сопротивления будет так же равна сумме работ отдельных механизмов т.е.

Учитывая, что

получим

(6.20)

При равенстве всех КПД входящих механизмов, т.е. получим .

Если работа движущих сил на входе каждого механизма одинакова, т.е. , то КПД сложного механизма будет

6.8 Кпд механизма передачи вращения.

Вращение – наиболее часто применяющийся вид движения ведущего звена, который легко преобразуется в другие виды движения. Поэтому механизмы передачи вращения (редукторы и мультипликаторы) получили широкое распространение и входят в состав большинства механизмов.

Рассмотрим схему механизма передачи вращения в общем виде (Рис 6.2в). На этом рисунке обозначены - угловые скорости ведущего и ведомого звена соответственно, - моменты движущих сил и сил полезного сопротивления. КПД такого механизма по определению будет