6.4 Уравнение движения механизма в конечной форме

Приведение всех сил и моментов, действующих на механизм, а так же всех масс и моментов инерции к одной приведенной силе (приведенному моменту) и одной приведенной массе (приведенному моменту инерции) позволяет описать движение механизма одним уравнением, которое может быть записано либо в конечной (интегральной) форме, либо в виде дифференциального уравнения (дифференциальная форма).

Для вывода уравнения движения механизма в конечной форме воспользуемся известной из теоретической механики теоремой об изменении кинетической энергии механизма

Где и -кинетические энергии механизма в конце и вначале работы соответственно;

- работа всех сил, действующих на механизм за этот промежуток времени, которую, в свою очередь, можно представить как

Где - работа движущих сил;

- работа сил полезных сопротивлений;

- работа сил вредных сопротивлений.

Тогда уравнение движения механизма в конечной форме запишется

(6.7)

Приводя массы звеньев механизма и силы, действующие на механизм к данной точке или к данному звену, это уравнение можно представить в двух формах: форме уравнения сил и уравнения моментов.

Уравнение в форме сил

Мощность всех сил, действующих на механизм можно представить (выражение 6.4)

.

Элементарная работа приведенной силы на перемещении точки приведения будет

Где - дуговая координата точки приведения.

Тогда, приводя все массы звеньев механизма к одной приведенной массе, сосредоточенной в точке приведения, теорему об изменении кинетической энергии можно записать

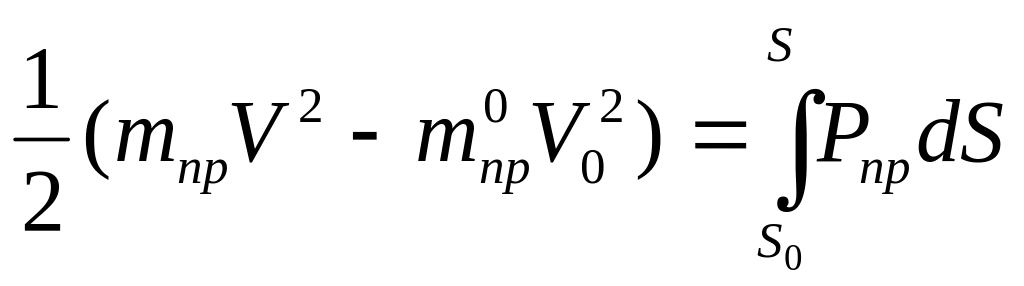(6.8)

Где - приведенные массы в начале и в конце движения механизма,

- скорости точки приведения.

Уравнение в форме моментов выводится аналогично.

Выражение для мощности всех сил будет

Элементарная работа всех сил

Откуда ,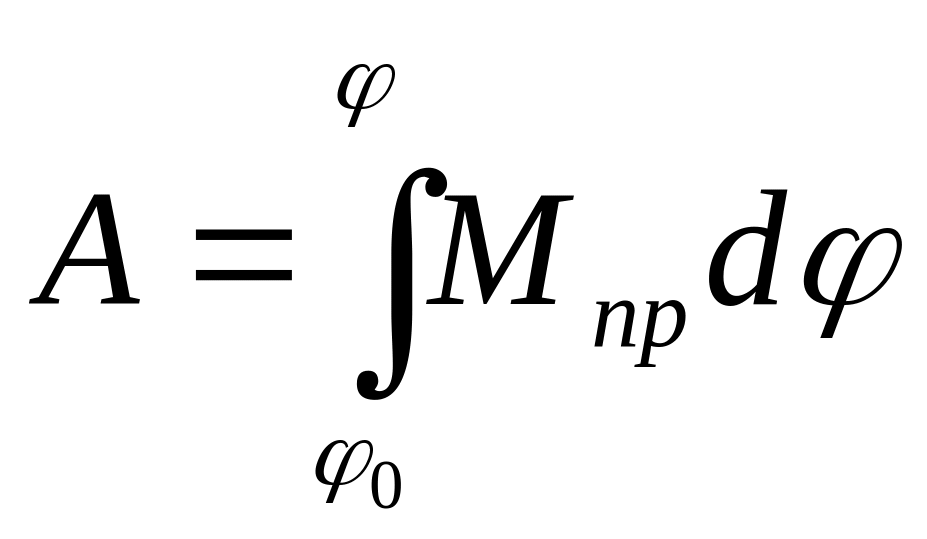

Где - элементарный угол поворота звена приведения.

Приводя все массы механизма к приведенному моменту инерции можно записать уравнение движения механизма в конечной форме в форме моментов

(6.9)

6.5 Три стадии движения механизма

Движение любого механизма можно условно разделить на три основные стадии: разбег, установившееся движение и останов.

Разбег (пуск) – на этой стадии движения скорость ведущего звена увеличивается от 0 до установившегося (рабочего) значения. В начальный момент времени кинетическая энергия механизма равна нулю. Тогда основное уравнение движения в интегральной форме (6.7) запишется

Откуда (6.10)

Т.е. на этой стадии движения механизма работа движущих сил идет на преодоление сил полезного и вредного сопротивления и на увеличения кинетической энергии механизма до установившегося значения. Для сокращения времени пуска механизма и облегчении его вывода на рабочий режим часто выключают силы полезного сопротивления (режим холостого хода). Тогда и уравнение (6.10) запишется

Установившееся движение - скорость ведущего звена остается постоянной (равновесное движение) или колеблется около среднего значения (неравновесное движение). При равновесном движении кинетическая энергия механизма в этом режиме остается постоянной. При неравновесном движении постоянной остается среднее за период значение кинетической энергии. Тогда из уравнения (6.10) получим

(6.11)

При неравновесном движении в установившемся режиме скорость начального звена остается в среднем постоянной, но внутри цикла изменяется от минимального до максимального значения т.е.

.

Неравномерность вращения ведущего звена оценивается коэффициентом неравномерности вращения

(6.12)

Который характеризует размах колебаний угловой скорости ведущего звена по отношению к среднему значению.

Для каждого вида механизмов эта величина задается нормативными документами. Так для металлорежущих станков , для дизельного двигателя - и т.д. Учитывая что можно принять

(6.13)

Тогда 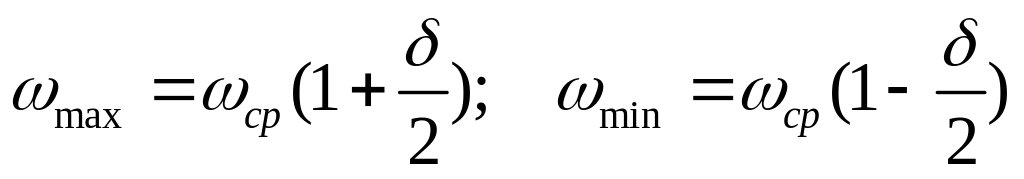(6.14)

Т.е. отличие максимальной и минимальной скорости вращения от средней составляет меньше двух процентов.

Останов (выбег) - на этом этапе движения скорость ведущего звена уменьшается от установившейся до нуля при этом движущие силы отключаются, т.е. . Тогда основное уравнение движения механизма (6.7) запишется

Для уменьшения времени остановки иногда используют специальные тормозные устройства, создающие силы противодействующие движению механизма, работа которых . Тогда получим

(6.15)