5.14 Выбор оптимальных коэффициентов смещения.

При назначении коэффициентов смещения и для любой передачи должны быть выполнены следующие три условия:

1. отсутствие подрезания;

2. отсутствие заострения;

3. непрерывность зацепления.

Первое условие применительно к шестерне выполняется, если ее коэффициент смещения превосходит свой минимальный уровень . Второе и третье условия ограничивают коэффициент смещения шестерни верхними пределами и (отсутствие заострения зуба и необходимым коэффициентом перекрытия ). Эти пределы неодинаковы, и для расчета зубчатой передачи важен тот , который имеет меньшее значение. Таким образом, коэффициент смешения шестерни надо назначать так, чтобы соблюдалось соотношение

.

Аналогично для колеса

.

Внутри указанных пределов коэффициенты смещения надо назначать так, чтобы зависящие от них качественные показатели передачи (плавность хода, износостойкость, прочность и т.д.) имели бы оптимальные значения. При этом надо учитывать конкретные условия работы передачи: быстроходность, характер нагрузки, смазка, материалы шестерни и колеса и т.д.

Для передачи с числом зубьев и можно построить в координатах и область допустимых значений коэффициентов смещения

(Рис 5.14). Эта область ограничена линиями

составляющими блокирующий контур. Допустимые значения коэффициентов смещения содержаться внутри блокирующего контура. Помимо блокирующего контура могут быть показаны и другие вспомогательные линии: и т.д.

В справочниках по расчету зубчатых передач приводятся блокирующие контура и рекомендации по выбору коэффициентов смещения.

Рис. 5.14

5.15 Косозубые и шевронные цилиндрические передачи

В цилиндрических колесах с прямыми зубьями соприкосновение двух сопряженных профилей происходит по прямой линии, параллельной осям колес по всей длине зуба. Если при изготовлении зуба были допущены какие-либо погрешности (неточность профиля, непостоянство шага и т.д.), то эти погрешности могут значительно ухудшить условия работы зубчатой передачи, в частности, например, усиливать шум. Кроме того, как было показано выше, коэффициент перекрытия зубчатых колес с прямыми зубьями ограничен весьма узкими пределами ( ), вследствие чего вся нагрузка распределяется не более чем на две пары зубьев. Это приводит к тому, что применение прямозубых цилиндрических передач, даже при высокой точности изготовления, ограничивается окружными скоростями V<15m/c.

Для увеличения плавности работы зубчатой передачи, уменьшения габаритов, уменьшения влияния погрешности изготовления и увеличения коэффициента перекрытия применяют косозубые и шевронные передачи.

У косозубых и шевронных колес (Рис 5.15а,б) зубья наклонены под некоторым углом к образующей делительного цилиндра, но оси колес являются при этом параллельными.

Рис. 5.15

Нарезание косозубых колес может производиться прямозубой рейкой, как и при изготовлении прямозубых колес; наклон зуба получают поворотом инструмента относительно заготовки на угол . При этом профиль косого зуба в нормальном к его оси сечении будет таким же, как и в прямозубом колесе.

Рассмотрим сечение зубчатого колеса начальным цилиндром (Рис 5.16). Сечение зуба на поверхности этого цилиндра образует винтовую линию (ас), образующей с осью колеса угол -угол скручивания. Дуга , соответствующая этому углу – дуга скручивания. Как видно из Рис 5.16, дуга скручивания определится как

.

Рис. 5.16

В плоскости перпендикулярной оси колеса зацепление происходит так же как в прямозубом колесе, но в каждый момент времени в зацеплении участвуют различные точки профилей. Поэтому влияние погрешности изготовления колеса сказываются значительно меньше, чем для прямозубого зацепления. Полная дуга зацепления по сравнению с прямозубым колесом будет увеличена на величину дуги скручивания

,

Где - дуга зацепления, соответствующая прямозубому колесу.

При одинаковом угловом шаге коэффициент перекрытия будет

(5.31)

Где - коэффициент перекрытия прямозубого колеса с таким же угловым шагом. Как видно из формулы (5.31) коэффициент перекрытия косозубого колеса значительно больше, чем прямозубого и может достигать величины . Следовательно, нагрузка в косозубом колесе распределяется на большее число зубьев, что увеличивает плавность и бесшумность работы зацепления, а так же увеличивает допустимую окружную скорость и уменьшает нагрузку на зуб. Поэтому косозубые колеса широко применяются для высокоскоростных передач.

По аналогии с прямозубым, в косозубом колесе различают основной, начальный, делительный цилиндры. А так же цилиндры вершин и впадин.

Линия пересечения боковой поверхности зуба с поверхностью делительного цилиндра называется – делительной линией зуба. Угол между делительной линией зуба и образующей делительного цилиндра – делительный угол наклона зуба. На делительном цилиндре обычно различают два шага:

- делительный окружной шаг, измеряемый по дуге окружности в торцевом сечении в плоскости перпендикулярной оси колеса.

-делительный нормальный шаг, измеряемый перпендикулярно винтовой линии.

Иногда вводят осевой шаг - , измеряемый в плоскости осевого сечения колеса.

Если развернуть делительный цилиндр, как показано на Рис 5.17, то соотношение между этими величинами будут:

(5.32)

Соответственно вводят окружной модуль- , нормальный модуль- и осевой модуль - , соотношения между которыми определяться согласно формулам (5.32)

(5.33)

Так как нарезание зубьев косозубого колеса выполняется стандартной рейкой, установленной под углом к оси заготовки, за стандартный обычно принимается нормальный модуль.

Рис. 5.17

Основные размеры косозубого колеса, нарезанные без смещения, определяются следующими выражениями:

1. Межосевое расстояние

(5.34)

2. Диаметр делительного цилиндра

(5.35)

3) Диаметр цилиндра вершин

(5.36)

4. Диаметр цилиндра впадин

(5.37)

5. Угол наклона винтовой линии на цилиндре диаметром

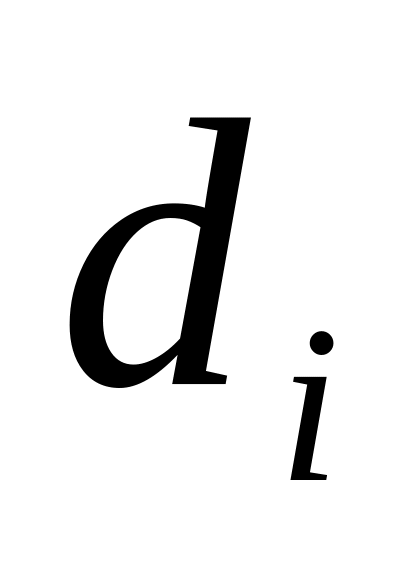
(5.38)

Косозубые цилиндрические колеса, изготовленные методом обкатки, имеют правильный эвольвентный профиль только в плоскости обкатки (в торцевом сечении). В нормальном сечении профиль отличается от эвольвентного. Однако при расчетах этим пренебрегают, считая, что нормальный профиль зуба косозубого колеса соответствует эвольвентному профилю некоторого условного эквивалентного прямозубого колеса. Радиус делительной окружности эквивалентного колеса принимают равным наибольшему радиусу кривизны эллипса, образуемого сечением делительного цилиндра плоскостью NN перпендикулярной винтовой линии на делительном цилиндре (Рис 5.18).

Рис. 5.18

Полуоси эллипса, как видно из Рис 5.18, равны:

Тогда радиус эквивалентного прямозубого колеса будет

Число зубьев эквивалентного колеса найдем, полагая что

.

Так как диаметр делительной окружности равен

Число зубьев эквивалентного колеса будет

(5.39)

Таким образом, косозубое колесо при расчетах можно условно заменить прямозубым эквивалентным колесом с числом зубьев .

Учитывая, что минимальное число зубьев для прямозубого колеса, нарезаемого без смещения, при отсутствии подрезания определяется формулой (5.20), аналогичная формула для косозубого колеса, с учетом (5.39) будет

(5.40)

Следовательно, минимальное число зубьев косозубого колеса может быть значительно меньше, чем для прямозубого, что позволяет уменьшить габариты передачи и увеличить прочность зубьев. Так при , .

Недостатком косозубого зацепления по сравнению с прямозубым является появление осевых усилий, передающиеся на опоры колес.

На Рис 5.19а показано распределение нагрузки в точке зацепления прямозубого колеса.

Усилие Р передается по линии зацепления NN и раскладывается на радиальную и тангенциальную составляющие, соотношение между которыми будет определяться углом зацепления .

(5.41)

Для косозубого колеса (Рис 5.19б) суммарное передаваемое усилие Р будет раскладываться на три составляющие: тангенциальную , передающую крутящий момент, радиальную и осевую составляющие, соотношения между которыми, как видно из Рис 5.19б, будет:

(5.42)

Для компенсации осевых нагрузок на опоры косозубых колес применяют шевронные колеса, представляющие собой два косозубых колеса с противоположным направлением зубьев (Рис 5.15б).

Рис. 5.19