§12 Линейная зависимость и линейная независимость системы строк, столбцов.

Определение 1. Пусть R (R ). Выражение вида , где R, , будем называть линейной комбинацией столбцов (строк) с коэффициентами .

Запись: ЛК будет означать, что столбец (строка) является линейной комбинацией столбцов (строк) .

Определение 2 . Совокупность столбцов (строк) R (R ) будем называть линейно зависимой, если существуют числа R, не равные нулю одновременно и такие, что (1).

В противном случае совокупность будем называть линейно независимой.

Таким образом, одна и та же совокупность столбцов (строк) не может быть одновременно и линейно зависимой, и

линейно независимой.

Заметим, что в равенстве (1) ноль означает нулевой столбец, если - столбцы, и нулевую строку, если - строки.

Пример. Пусть . Очевидно, справедливо равенство: . Следовательно, совокупность строк линейно зависимая.

Часто бывает удобнее пользоваться другим определением линейно независимой совокупности, разумеется, равносильным определению 2.

Определение3. Совокупность столбцов (строк) R (R ) будем называть линейно независимой, если

из равенства нулевому элементу линейной комбинации этих столбцов (строк) следует равенство нулю всех коэффициентов этой линейной комбинации, т.е. из равенства следует, что .

Пример. Пусть . Составим линейную комбинацию этих столбцов и приравняем её к нулевому столбцу: .

Рассмотрим определитель этой системы: . Следовательно, эта система линейных однородных алгебраических уравнений имеет единственное, т.е. нулевое решение .

Таким образом, из равенства следует, что , и, следовательно, совокупность столбцов линейно независимая.

Теорема 1. Совокупность столбцов (строк), содержащая нулевой столбец (нулевую строку) линейно зависима.

Доказательство. Пусть в совокупности R (R ) -ый элемент нулевой, т.е. . Тогда, очевидно, справедливо равенство , причём 1- -ый коэффициент не равен 0.

Таким образом, совокупность столбцов (строк) линейно зависимая по определению 2.

Теорема 2. Если к линейно зависимой совокупности столбцов (строк) добавить ещё несколько, то получившаяся совокупность будет также линейно зависимая.

Доказательство. Пусть совокупность столбцов (строк) R (R ) линейно зависимая, т.е. существуют числа R, не равные нулю одновременно и такие, что . Покажем, что тогда

совокупность R (R ) также линейно зависимая.

Действительно, очевидно, справедливо равенство , причём не все коэффициенты этой линейной комбинации равны 0, т.к. не все коэффициенты равны нулю.

Теорема 3. Если из линейно независимой совокупности столбцов (строк) удалить несколько, то получившаяся совокупность будет также линейно независимой.

Доказательство проведём от противного с использованием теоремы 2. Пусть совокупность столбцов (строк) R (R ) линейно независимая, а совокупность линейно зависимая.

Тогда по теореме 2 исходная совокупность столбцов (строк) будет также линейно зависимая, что противоречит условию, и теорема доказана.

Теорема 4. Критерий линейной зависимости. Для того чтобы совокупность столбцов (строк) была линейно зависимой, необходимо и достаточно, чтобы один из элементов этой совокупности был линейной комбинацией остальных.

Доказательство.

Необходимость. Пусть совокупность столбцов (строк) R (R ) линейно зависимая, т.е. существуют числа R, не равные нулю одновременно и такие, что , и пусть для определённости . Тогда из последнего равенства получаем:

, и необходимость доказана.

Достаточность. Пусть , . Тогда справедливо равенство: , причем . Следовательно, совокупность столбцов (строк) линейно зависимая по определению 2, и достаточность доказана.

Теорема 5. Если после добавления к линейно независимой совокупности столбцов (строк) R (R ) столбца (строки) R (R ) новая совокупность становится линейно зависимой, то

добавленный элемент есть линейная комбинация элементов исходной совокупности, т.е.

ЛК .

Доказательство. По условию совокупность линейно зависимая. Это означает, что существуют числа R, не равные нулю одновременно и такие, что Покажем, что . Пусть это не так, т.е. . Тогда из равенства (2) следует: , причём среди чисел есть ненулевые, т.к. , а не равны нулю одновременно. Тогда из определения 2 следует, что совокупность линейно зависимая, а это противоречит условию.

Таким образом, доказали, что . Тогда из равенства (2) получаем: , и теорема 5 доказана.

Теорема 6. О линейной зависимости линейных комбинаций.

Пусть даны столбцы (строки) R (R ) и пусть столбцы (строки) являются линейными комбинациями . Тогда если , то совокупность линейно зависимая, т е. если число линейных комбинаций больше числа комбинируемых элементов, то эти линейные комбинации линейно зависимы.

Доказательство проведём методом математической индукции по числу комбинируемых элементов, т.е. по .

База математической индукции. Пусть . Тогда по условию . Если , то , и совокупность линейно зависимая по теореме 1. Если , то , и совокупность линейно зависимая по теореме 4, т.к. ЛК .

Следовательно, совокупность линейно зависимая по теореме 2, и база доказана.

Индукционный переход. Докажем, что утверждение теоремы справедливо для случая, когда число комбинируемых элементов равно , если она верна для случая, когда число комбинируемых элементов равно . Пусть

.

Если , то являются линейными комбинациями , и, следовательно,

совокупность линейно зависимая по индукционному предположению. Пусть теперь один из этих коэффициентов, например, не равен нулю.

Рассмотрим теперь совокупность столбцов (строк) таких, что:

.

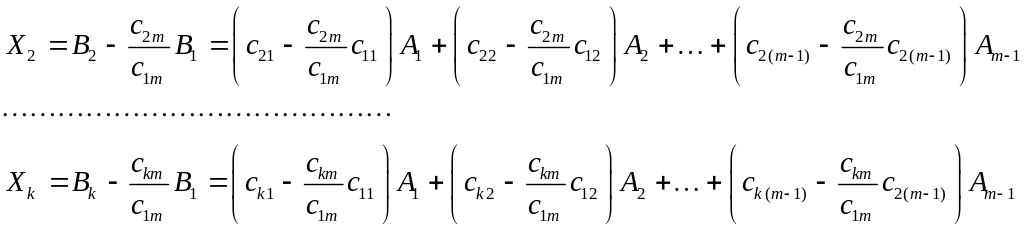Эта совокупность является линейно зависимой по индукционному предположению, т.к. ЛК , причём число линейных комбинаций больше числа комбинируемых элементов , т.к. . Следовательно, существуют числа R, не равные нулю одновременно и такие, что

.

Отсюда следует, что совокупность линейно зависимая, т.к. коэффициенты не равны нулю одновременно. В этом случае величина первого коэффициента не имеет значения, т.к. ненулевой коэффициент имеется среди последних коэффициентов. Теорема 6 доказана.

Теорема 7. О базисных столбцах (строках) матрицы.

Базисные столбцы (строки) матрицы линейно независимы. Остальные столбцы (строки) матрицы являются их линейными комбинациями.

Доказательство. Пусть дана матрица , и пусть её базисный минор стоит в первых строках и первых столбцах, т.е. и . Таким образом, базисными являются столбцы .

I. Докажем, что совокупность является линейно независимой. Составим линейную комбинацию этих столбцов и приравняем её к нулевому столбцу:

. Если выполняются все равенств, то, в частности, выполняются и первые из них, т.е. следующие: . Таким образом, числа являются решениями квадратной системы линейных однородных алгебраических уравнений, определитель которой не равен нулю. По теореме Крамера такая система имеет единственное нулевое решение, т.е. . Итак, из равенства следует, что . Следовательно, по определению 3 совокупность столбцов линейно независимая.

Аналогично доказывается линейная независимость базисных строк, т.е. совокупности .

I I. Теперь докажем, что все остальные столбцы, т.е. столбцы являются линейными комбинациями базисных. Пусть . Рассмотрим определитель , где . Если , то этот определитель является минором матрицы порядка , и потому равен нулю. Если , то этот определитель не является минором матрицы , но он равен нулю как определитель, матрица которого содержит две одинаковые строки. Таким образом, при любом ( )справедливо равенство . Разложим определитель по элементам -ой строки:

(3)

Здесь означает алгебраическое дополнение элемента в определителе . Напомним, что алгебраическое дополнение элемента не зависит от элементов той строки, в которой стоит этот элемент, т.е. в данном случае от элементов -ой строки. Кроме того, . Введём обозначения: для .

Ещё раз отметим, что эти обозначения корректны, т.к. алгебраическое дополнение элемента не зависит от элементов -ой строки, что и отражено в обозначениях. Тогда равенство (3) принимает вид:

, откуда получаем: для любого , т.е.

, где

, и теорема полностью доказана.

Аналогично доказывается, что небазисные строки являются линейными комбинациями базисных строк, т.е. .

Следствие 1. Для того чтобы столбцы (строки) одинаковой высоты (длины) были линейно независимы, необходимо и достаточно, чтобы ранг матрицы, составленной из них, был бы равен их числу.

Иначе: 1)если R , то совокупность линейно независимая .

2)если R , то совокупность линейно независимая .

Доказательство проведём для столбцов. Доказательство для строк аналогично.

Необходимость. Пусть линейно независимы и пусть . Тогда столбцов, входящих в базисный минор, линейно независимы, а остальные столбцы являются их линейными комбинациями.

Пусть, для определённости, совокупность линейно независимая. Тогда по теореме 7 ЛК , и по теореме 4 совокупность линейно зависима. Тогда по теореме 2 линейно зависимой будет и совокупность , что противоречит условию.

Достаточность. Пусть . Тогда все столбцы этой матрицы базисные, и потому совокупность линейно независимая по теореме 7.

Следствие 2. Для того чтобы столбцы (строки) одинаковой высоты (длины) были линейно зависимы, необходимо и достаточно, чтобы ранг матрицы, составленной из них, был бы меньше их числа.

Иначе: 1)если R , то совокупность линейно зависимая .

2)если R , то совокупность линейно зависимая .

Доказательство проведём для столбцов. Доказательство для строк аналогично.

Необходимость. Пусть совокупность линейно зависимая и пусть неравенство

неверно. Тогда справедливо равенство , т.к. ранг матрицы не может быть больше числа её столбцов, т.е. . Тогда по следствию 1 совокупность линейно независимая, что противоречит условию.

Достаточность. Пусть . Тогда совокупность линейно зависимая, т.к. в противном случае по следствию 1 выполнялось бы равенство , что противоречит условию.

Следствие 3. Ранг матрицы равен максимальному числу линейно независимых столбцов (строк) этой матрицы.

Доказательство. Из теоремы 7 следует, что если , то существует линейно независимая совокупность из столбцов этой матрицы, а именно, состоящая из базисных столбцов. Поэтому для доказательства следствия 3 достаточно доказать, что любая совокупность столбцов этой матрицы линейно зависима, если .

Действительно, каждый столбец этой совокупности есть линейная комбинация базисных, а число базисных столбцов равно рангу матрицы, т.е. . Следовательно, по теореме 6 совокупность линейно зависимая, т.к. число линейных комбинаций больше числа комбинируемых столбцов. Следствие 3 доказано. Доказательство для строк аналогично.

Следствие 4. Для того чтобы определитель квадратной матрицы был равен нулю, необходимо и достаточно, чтобы её столбцы (строки) были линейно зависимыми.

Необходимость. Если определитель квадратной матрицы -го порядка равен нулю, то её единственный минор –го порядка, т.е. . Следовательно, ненулевые миноры, в частности, базисный имеют порядок меньший , и таким образом, . Тогда по следствию 2 (достаточность) столбцы этой матрицы линейно зависимые. Доказательство для строк аналогично.

Достаточность. Если столбцы матрицы линейно зависимые, то по следствию 2 (необходимость)

ранг этой матрицы меньше их числа: . Следовательно, единственный минор –го порядка матрицы , т.е. . Доказательство для строк аналогично.

Пример. В §11 было показано, что . Базисный минор этой матрицы стоит в левом верхнем углу: . Следовательно, столбцы - базисные, а потому и линейно независимые. Столбцы есть их линейные комбинации.

.

Базисными строками являются первые три: . Последняя строка есть их линейная комбинация:

.