
- •6.050403 “Прикладне матеріалознавство”
- •Лабораторна робота №6 підбір емпіричних формул у вигляді поліному з застосуванням методу середніх квадратів
- •6.1. Загальні відомості
- •6.2 Завдання на підготовку до лабораторної роботи
- •6.3 Контрольні питання
- •7.2 Завдання на підготовку до лабораторної роботи
- •7.3 Контрольні питання
- •7.4 Матеріали і устаткування
- •7.5 Вказівки з техніки безпеки
- •7.6 Порядок виконання лабораторної роботи
- •7.8 Література
- •Лабораторна робота №8 кореляційний аналіз
- •8.1 Загальні відомості
- •8.2 Завдання на підготовку до лабораторної роботи
- •8.3 Контрольні питання
- •8.4 Матеріали і устаткування
- •8.5 Вказівки з техніки безпеки
- •8.6 Порядок виконання лабораторної роботи
- •8.8 Література
- •Лабораторна робота №9 оформлення результатів наукової роботи
- •9.1 Загальні відомості
- •9.2 Завдання на підготовку до лабораторної роботи
- •9.3 Контрольні питання
- •Додаток а Правила із техніки безпеки при виконанні лабораторних робіт
- •Вимоги безпеки перед початком роботи
- •Вимоги безпеки під час виконання роботи
- •Вимоги безпеки в термічній та препараторських лабораторіях
7.2 Завдання на підготовку до лабораторної роботи
Для виконання лабораторної роботи та пояснення результатів експериментів необхідно пропрацювати загальні відомості до даної роботи та контрольні питання.
7.3 Контрольні питання
7.3.1 Яку модель вважають адекватною?
7.3.2 На якій умові ґрунтуються критерії адекватності моделі?
7.3.3 В чому полягає сутність перевірки моделі на адекватність?
7.3.4 За яких умов використовують критерій Фішера для перевірки адекватності моделі?
7.3.5 Описати методику застосування критерію Фішера для перевірки адекватності моделі?
7.3.6 Яким чином перевіряють однорідність дисперсії?
7.3.7 В чому полягає нульова гіпотеза при перевірці моделі на адекватність?
7.3.8 Описати методику застосування графічного методу перевірки моделі на адекватність.
7.3.9 Описати методику використання коефіцієнта кореляції між сусідніми відхиленнями для перевірки моделі на адекватність.
7.3.10 Описати методику визначення істотності коефіцієнтів моделі порівнянням їх абсолютної величини з довірчим інтервалом.
7.3.11 Описати методику визначення істотності коефіцієнтів моделі за допомогою t - критерію Ст’юдента.
7.4 Матеріали і устаткування
Результати сумісних вимірювань для виконання лабораторної роботи студенти отримують у викладача та можуть використати результати попередніх робіт.
7.5 Вказівки з техніки безпеки
Роботу виконують з дозволу викладача у відповідності з інструкціями із ТБ (додаток А).
7.6 Порядок виконання лабораторної роботи
Ознайомитись з методами оцінювання адекватності математичних залежностей. За результатами експериментальних даних або з використанням даних попередніх робіт підібрати емпіричну формулу застосувавши метод найменших квадратів, перевірити її адекватність та істотність коефіцієнтів.
7.7 Зміст звіту
Мета роботи, загальні відомості. Розрахунок необхідних величин. Аналіз отриманих результатів. Висновки.
7.8 Література
1. Крутов В.И. Основы научных исследований [Текст]: Учеб. для техн. вузов / В.И. Крутов, И.М. Грушко, В.В. Попов и др. Под ред. В.И. Крутова, В.В. Попова.– М.: Высш. шк., 1989. – С. 313-316.
2. Дорожовець М. Опрацювання результатів вимірювань[Текст]: навч. посібник / М. Дорожовець – Львів: Видавництво Національного університету “Львівська політехніка”, 2007.– С. 547-555.
Лабораторна робота №8 кореляційний аналіз
Мета роботи: Освоїти методику розрахунку коефіцієнта кореляції й проведення кореляційного аналізу
8.1 Загальні відомості
Особливістю матеріалознавства є розмаїтість досліджуваних структур, властивостей матеріалів та технологічних процесів, що застосовуються при їх використанні. До них відносяться процеси гартування, відпускання, цементації і ін. При проведенні наукових досліджень в області матеріалознавства також розглядаються питання організації виробництв, оптимізації керування технологічними процесами, конструювання й експлуатації печей та іншого встаткування. Тому при наукових дослідженнях в області матеріалознавства застосовують методи, запозичені зокрема з математики. В даній роботі розглянемо застосування кореляційного аналізу.
Нехай деякий об'єкт характеризується двома величинами X і Y між якими можуть існувати залежностей функціональна, статистична, кореляційна.
Функціональна залежність – це така залежність, коли кожному значенню величини Х відповідає єдине значення величини Y. Залежність задається у вигляді функції y = f(x).
Статистична залежність – це така залежність, коли кожному значенню величини Х відповідає статистичний розподіл величини Y. Ця залежність задається у вигляді кореляційної таблиці.
Кореляційна
залежність – це окремий випадок
статистичної залежності, коли кожному
значенню величини Х відповідає середнє
значення величини Y (![]() )
і зв'язок між ними досить добре описується
функцією
=f(x),
яка називається рівнянням регресії Y
по Х. Аналогічно, якщо кожному значенню
величини Y відповідає середнє значення
)
і зв'язок між ними досить добре описується
функцією
=f(x),
яка називається рівнянням регресії Y
по Х. Аналогічно, якщо кожному значенню
величини Y відповідає середнє значення
![]() ,
то тоді ця функція називається рівнянням
регресії Х по Y. Кореляційний аналіз
дозволяє на підставі вибірки досліджувати
стохастичну залежність між властивостями
досліджуваного об'єкта. Порядок проведення
кореляційного аналізу наступний:
,
то тоді ця функція називається рівнянням
регресії Х по Y. Кореляційний аналіз
дозволяє на підставі вибірки досліджувати
стохастичну залежність між властивостями
досліджуваного об'єкта. Порядок проведення
кореляційного аналізу наступний:
- встановлення наявності зв'язку між властивостями досліджуваного об'єкта за допомогою діаграм розсіювання;
- відбір факторів, що чинять найбільший вплив на досліджуваний об'єкт;
- визначення характеру зв'язку, його напрямку і форми, вибір математичного рівняння для описання виявленого зв'язку;
- визначення параметрів рівняння й показників тісноти зв'язку;
- статистична оцінка вибіркових показників зв'язку.
Наприклад, щоб попередньо визначити наявність кореляційного зв'язку між х і у, наносять точки на графік і будують так зване кореляційне поле. За щільністю групування точок біля прямої або кривої можна бачити наявність кореляційного зв'язку. Так, з рис. 8.1 а видно, що експериментальні дані мають явний зв'язок між х і у, і їх можна апроксимувати прямою АБ, рівновіддаленою від точок, що знаходяться зліва і справа від неї. Експериментальні дані, зображені на рис. 1 б, кореляційного зв'язку не мають.

а – зв’язок існує; б – зв’язку немає
Рисунок 8.1 ‑ Визначення наявності кореляційного зв’язку.
При побудові діаграм розсіювання, необхідно ретельно вибирати шкали горизонтальної й вертикальної осей, оскільки при їхньому неправильному виборі можна одержати помилкову інтерпретацію інформації.
Наявність високого коефіцієнта кореляції не обов'язково вказує на існування причинно-наслідкового взаємозв'язку між змінними.
В одному обстеженні було встановлено, що між індексом споживчих цін і числом пожеж існує сильна позитивна кореляція, тоді зі зменшенням індексу споживчих цін спостерігалося б зменшення числа випадкових загорянь. Проте мабуть це не так. Для скорочення числа випадків загорянь варто було б зосередитися на своєчасному очищенню сміттєвих кошиків від сміття, що може з'явитися джерелом загорянь. При обчисленні коефіцієнта кореляції між двома змінними іноді може проявлятися сильна кореляція, що не підкріплюється або підкріплюється занадто слабкими причинно-наслідковими залежностями між ними. Кореляція такого роду називається помилковою кореляцією.
Тіснота лінійного зв'язку в кореляційному аналізі характеризується спеціальним відносним показником – коефіцієнтом кореляції Браве і Пірсона.
Для вивчення наявності зв'язку між ознаками Х і Y досліджуваного об'єкта необхідно побудувати діаграму розсіювання, а для кількісної оцінки статичного зв'язку за експериментальними даними широко використовувати вибірковий коефіцієнт кореляції, що дозволяє об'єктивно оцінити ступінь залежності
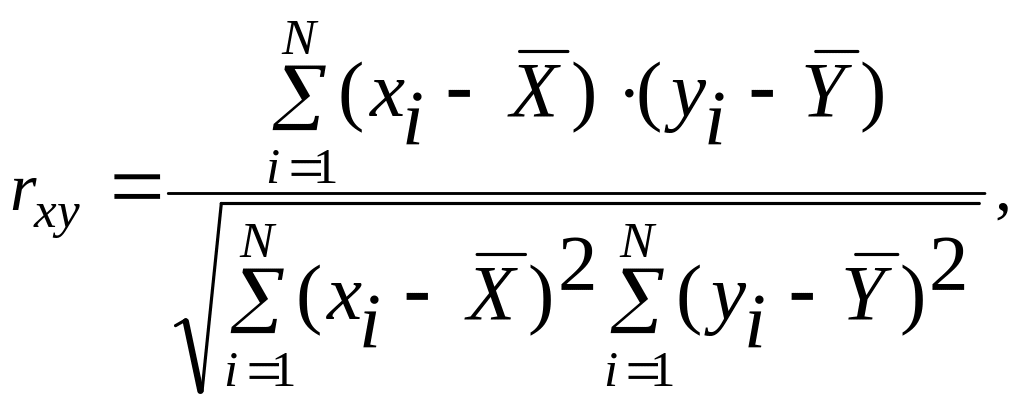 (8.1)
(8.1)
де
![]() – коефіцієнт кореляції; N
– кількість парних спостережень у
вибірці;
– коефіцієнт кореляції; N
– кількість парних спостережень у
вибірці;
![]() і
і
![]() – змінні (
– фактор,
– показник якості);
– змінні (
– фактор,
– показник якості);
![]() і
і
![]() – середні арифметичні відповідно
– фактора і
– показника якості.
– середні арифметичні відповідно
– фактора і
– показника якості.
Розрахунок можна виконати в зручному для обчислень виді за формулою (8.2)
 (8.2)
(8.2)
або використовуючи наступні формули (8.3 – 8.6)
![]() , (8.3)
, (8.3)
 , (8.4)
, (8.4)
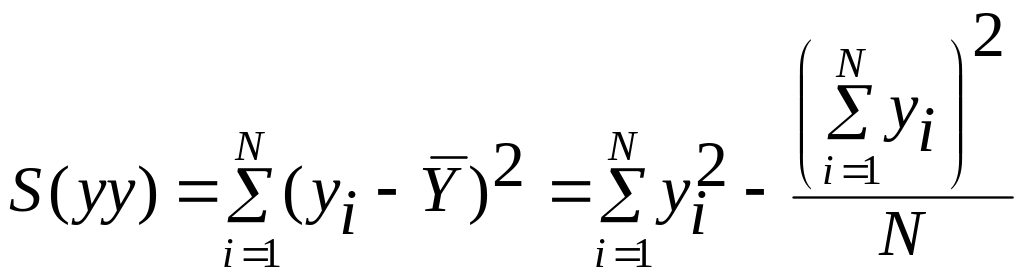 , (8.5)
, (8.5)
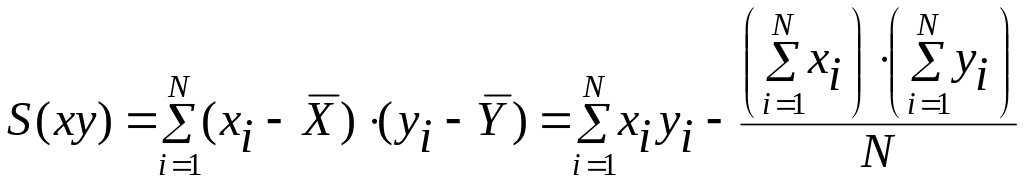 ,
(8.6)
,
(8.6)
де N – число пар вимірів; S(xy) – коваріація.
Для коефіцієнта кореляції двох випадкових змінних Х і У справедливо:
-1 +1, при = 1 є функціональна залежність – всі точки лежать на прямій (дві випадкові змінні тим сильніше корельовані, чим ближче значення до одиниці);
якщо = 0, то ознаки Х і У називаються некорельованими, тобто для двовимірної нормально розподіленої змінної спостерігається стохастична незалежність;
у випадку, > 0, говорять про позитивну кореляцію випадкових величин Х і У, а при < 0 – про негативну кореляцію.
Абсолютна величина | r | вказує на тісноту зв'язку.
Оцінити тісноту лінійного зв'язку можна за шкалою Чаддока (табл. 8.1).
Таблиця 8.1 ‑ Шкала Чаддока
Значення |r| |
0-0,1 |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
1 |
Наявність функціональної лінійної залежності |
немає |
слаб-ка |
по-мір-на |
помі-тна |
висо-ка |
дуже висо-ка |
пов-на |
Коефіцієнт кореляції близький до одиниці, не завжди свідчить про наявність кореляційної залежності між досліджуваними величинами. При оцінці коефіцієнта кореляції необхідно враховувати число пар спостережень N, за якими було проведено його обчислення, оскільки при невеликому числі пар спостережень N значення вибіркового коефіцієнта часто значно відрізняється від дійсного значення коефіцієнта кореляції.
Для обґрунтованих висновків про тісноту залежності між випадковими величинами Х і У за експериментальними даними, необхідно встановити значимість коефіцієнта кореляції, тобто перевірити гіпотезу про рівність коефіцієнта кореляції нулю (Н0: r= 0). Для нормально розподілених випадкових величин випадковість відхилення коефіцієнта кореляції від нуля здійснюють за допомогою t-розподілу Ст’юдента.
Для
цього спочатку висувають гіпотезу, про
те, що величини Х і У– некорельовані.
Потім за формулою (8.7) обчислюють
розрахункове значення
![]() й порівнюють його з табличним значенням
й порівнюють його з табличним значенням
![]() ,
знайденому по додатку Б при числі
ступенів волі f =N–2
і обраному рівні значимості q.
,
знайденому по додатку Б при числі
ступенів волі f =N–2
і обраному рівні значимості q.
![]() (8.7)
(8.7)
Якщо
![]() ,
то висунута гіпотеза про некорельованість
досліджуваних величин не підтверджується,
тобто між ними існує кореляційна
залежність.
,
то висунута гіпотеза про некорельованість
досліджуваних величин не підтверджується,
тобто між ними існує кореляційна
залежність.
Для вирішення питання про значимість коефіцієнта кореляції можна скористатися графіком (рис. 8.2), на якому є три області.

Рисунок 8.2 ‑ Графік для визначення значимості коефіцієнта кореляції
За розрахованим значенням і числом вимірів N знаходимо точку з координатами (N, r). Попадання вказаної точки в область:
А - обмежену нижньою кривою й осями координат, свідчить про не значимість коефіцієнта кореляції (про відсутність кореляційної залежності досліджуваних величин);
В - розташовану між двома кривими, свідчить про значимість коефіцієнта кореляції;
С – розташовану над верхньою кривою, свідчить про високу тісноту кореляційної залежності між величинами, що досліджуються.
Метод судження про існування кореляції за допомогою побудови діаграм розсіювання й обчислення коефіцієнта кореляції, описаний вище, називається кореляційним аналізом.
