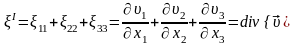- •1.Шар тензоры және кернеу девиаторы.
- •2.Илемдеу өңдірісінің негізгі технологиялық операциялары.
- •3.Қосиінді баспақтар. Орындалу механизмдері. Технологиялық белгілері бойынша классификациясы.
- •11.1Сурет. Қосиінді баспақтардың орындаушы механизмдерінін сұлбалары.
- •11.2 Сурет – Технологиялық қолданылуына байланысты қосиінді баспақтардың классификациясы.
- •1.Дайындама көлемінің өзгермеу принципі.
- •2.Илемдеу әдістері. Металды қарпу шарттары.
- •2.2 Сурет. Жанасу ұзындығын l анықтау (қарпу доғасының бойлық проекциясын)
- •3.Илемдеу орнақтары. Қолданылуы, классификациясы.
- •1.1 Сурет. Илем сортаменті
- •1.Деформация тензоры.
- •1)Кернеу тензоры. Еңкіш алаңдардағы кернеулерді анықтау.
- •1.3 Сурет – Элементарлы тетраэдр
- •3)Жетекті пневматикалық тоқпақтар. Қолданылуы. Классификациясы.Негізгі параметрлері. Тоқпақ пәк-нің жұмыс режімі.
- •1)Максималды жанама кернеулер және оның анықталуы.
- •2)Суықтай илемдеу.
- •3)Гидравликалық баспақтар. Жұмыс істеу принципі және есептеуі.
- •6.1 Сурет - Тоқпақтардың классификациясы
- •6.2 Сурет - Тоқпақтардың сұлбалары.
- •6.3 Сурет – Соғумен деформациялаудың пәк массалар қатынасына тәуелділігі
- •Илемдеу орнақтары. Қолданылуы, классификациясы.
- •Илемділік пішінөзгеруі кезіңдегі кернеулер және деформациялар арасыңдағы байланыс.
- •1) Дайындаманы тесіп, қалың қабырғалы гильза алу;
- •2) Гильзаны құбырға илемдеу;
- •3) Құбыр қалыңдығын әртүрлі және сопақ болмау үшін және ішкі, сыртқы беттерін жақсарту үшін илеу.
- •Құймасыз илемдеу.
- •1.Газды жағу үшін құралдары, олардың түрлері.
- •2. Соғу кезіңдегі созу операциясы. Созу кезіңдегі кермелеуді интенсификациялау әдістері. Созу процесінің түрлері.
- •3.Ыстықтайқалыптау баспақтары. Қолданылуы, құрылымының ерекшеліктері, жұмысы..
- •1..Деформация жылдамдығы және деформациялау жылдамдығы.
- •8.2 Сурет Тұтас ортаның ағысы
- •2.Металды сымдау процесінің негізі.
- •3.Илемдеу кезіңдегі деформация ошағы, металды біліктермен қарпу бұрышы, деформация ұзыңдығының аймағы және түйісу алаңы.
- •2.2 Сурет. Жанасу ұзындығын l анықтау (қарпу доғасының бойлық проекциясын)
- •1.Монокристалдың суық пластикалық деформациясы.
- •2.Сымдау орнағынынң негізгі түзілімдері. Сымдағыштар конструкциясы волок. Сымдаштардың қолдану аймағы.
- •3.Қосиінді баспақтардың сырғақтары және бағыттаушылары. Конструкциясы, материалдары және есептеуі.
- •15.6 Сурет. Баспақ сырғағы
- •- Билет
- •3... Жетекті пневматикалық тоқпақтар
- •1...Материалдарды ыстықтай және суықтай қө кемшіліктері және артықшылықтары.
- •2...Қаңылтырды қалыптаудың пішінөзгерту операциялары.
- •3...Бұрама баспақтар (Винтті баспақтар). Жұмыс істеу принципі және классификациясы.
- •6.1 Сурет - Тоқпақтардың классификациясы
- •6.2 Сурет - Тоқпақтардың сұлбалары.
- •6.3 Сурет – Соғумен деформациялаудың пәк массалар қатынасына тәуелділігі
- •1.Қаңылтырды кесу қайшылары. Конструкция ерекшеліктері және есептеуі.
- •2. Илемдеудің қарапайым процесі. Біліктерге әсер ететін күш бағыттары.
- •3.Сымдарды, жұқа қабырғалы құбырларды өндіру.
- •1.Созу операциялары. Созу түрлері.
- •2.1 Сурет Түзеткішпен ұзартудың сұлбасы
- •2.Қосиінді машиналардың бұлғақтары.
- •3.Профилдерді, шыбықтарды және құбырларды өндіру.
- •1.Серпімді және пластикалық деформация
- •2.Әдіп, шақтама, кенерме. Олардың қызметі, қалыптау кезіңде қолданылуы.
- •3.Тоқпақтар. Жұмыс істеу принципі. Классификациясы.
- •1.Серпімді және пластикалық деформация
- •6.1 Сурет - Тоқпақтардың классификациясы
- •6.2 Сурет - Тоқпақтардың сұлбалары.
- •6.3 Сурет – Соғумен деформациялаудың пәк массалар қатынасына тәуелділігі
- •1...Қорытпалар туралы жалпы түсінік.
- •2....Салқындату кезіндегі аустениттің диффузионды түрленуі. Тілімшелі және түйіршікті перлиттің түзілу сұлбасы. Олардың қасиеттерінің қысқаша сипаттамасы.
- •2.Машина жасау зауыттарын жобалаудағы жалпы талаптар. Өндірісті дайындау.
- •3.Қорытпалар ақаулары және құюдан, пісіруден және термиялық өңдеуден кейінгі өнімнің сапасын бақылау.
- •1)Полиморфты түрленусіз шынықтыру процессінің мазмұны. Қортыпалардың табиғи және жасанды ескіруі.
- •2) Бетінің жоғары қаттылығымен материалдар. Тозудың абразивті, шаршау және кавитациялық түрлеріне тұрақты материалдар.
1..Деформация жылдамдығы және деформациялау жылдамдығы.
Деформация
жылдамдығы тензоры.
Деформациялар
жылдамдықтары.
Қараушы кеңістігінде бекітілген
декарттық координаттар жүйесін хi
қолданайық. Тұтас орта қозғалатын
аймақта көлемі W
болатын элементі бөліп алайық және осы
көлемде орналасқын М
және N
нүктелеріне қарайық. Бөлінген М
нүктенің радиус-векторы
 болсын, ал оған жақын орналасқан N
нүктесінің радиус-векторы
болсын, ал оған жақын орналасқан N
нүктесінің радиус-векторы
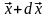 болсын (8.2 – сурет). М
нүктесінің жылдамдығы
болсын (8.2 – сурет). М
нүктесінің жылдамдығы
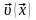 ,
ал көрші N
нүктесінің жылдамдығы
,
ал көрші N
нүктесінің жылдамдығы
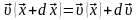 тең болсын, онда дифференциал мынаған
тең:
тең болсын, онда дифференциал мынаған
тең:
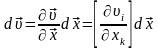 .
.
Тензорды
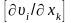 (
(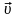 векторының векторлық аргумент бойынша
туындысы) симметриялық және қисық
симметриялық тензорлардың қосындысына
бөліп мынаны табамыз:
векторының векторлық аргумент бойынша
туындысы) симметриялық және қисық
симметриялық тензорлардың қосындысына
бөліп мынаны табамыз:
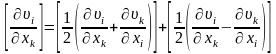 .
(8.3)
.
(8.3)

8.2 Сурет Тұтас ортаның ағысы
Осылай тензорды симметриялық және қисық симметриялық тензорлардың қосындысына бөле отырып N нүктесінің жылдамдығын былай табайық:
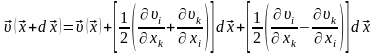 .
(8.4)
.
(8.4)
Үшінші қосындыны өзгертейік. Оқулық [1] келтірілген мәліметтерді пайдалана отырып қисық симметриялы тензорды мынандай түрге келтіруге болады:
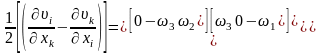 ,
,
мұндағы
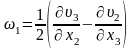 ;
;
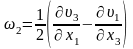 ;
;
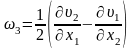 .
.
Жылдамдық
құйынын есептеудің формуласын еске ала
отырып, вектор
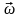 (сыңарлары
(сыңарлары
 )
жылдамдық өрісімен
мынандай теңдікпен байланысты екендігін
еске түсіреміз:
)
жылдамдық өрісімен
мынандай теңдікпен байланысты екендігін
еске түсіреміз:
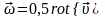 .
.
Осындай математикалық талдаудан кейін мынаны жазуға болады:
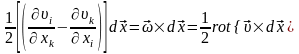 .
.
Анықталған формулаларды (8.4) теңдеуіне қойып мынандай теңдеуді аламыз:
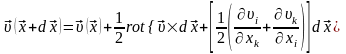 .
(8.5)
.
(8.5)
Жоғарыда
жазылған ең соңғы формула N
нүктесіндегі жылдамдық үш қосылғыштың
қосындысынан тұратынын көрсетеді.
Бірінші қосылғыш, ол элемент W-ның
үдемелі қозғалысының жылдамдығы
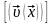 ,
екінші қосылғыш, ол қатты дененің
айналуымен байланысты жылдамдық
,
екінші қосылғыш, ол қатты дененің
айналуымен байланысты жылдамдық
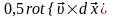 ,
ал үшінші қосылғыш, ол элементтің
илемділік деформациясымен байланысты
жылдамдық
,
ал үшінші қосылғыш, ол элементтің
илемділік деформациясымен байланысты
жылдамдық
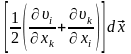 .
.
Деформация
жылдамдығының тензоры.
Мынандай симметриялық тензорды:
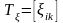 ,
(8.6)
,
(8.6)
мұндағы
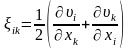 ,
(8.7)
,
(8.7)
деформация жылдамдығы тензоры деп атайды.
Осы тензордың сыңарларында қандай геометриялық мән бар екендігін қарайық.
t
уақытысына мынандай өсімшені берейік:
dt.
Онда ортаның бөлшектері мынандай өте
кішкентай мөлшерге орын ауыстырады:
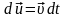 .
.
Орын
ауыстыру өрісіне
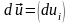 мынандай деформация тензоры сәйкес
келеді:
мынандай деформация тензоры сәйкес
келеді:
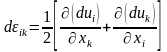 .
.
Деформация
сыңарларын
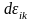 уақыт өсімшесіне dt
бөле отырып, осы dt-ны
нөльге ұмтылдырайық. Сонда алынатын
мынандай мөлшер:
уақыт өсімшесіне dt
бөле отырып, осы dt-ны
нөльге ұмтылдырайық. Сонда алынатын
мынандай мөлшер:
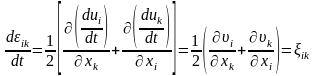 (8.8)
(8.8)
деформация жылдамдығы деп аталады.
Тензордың
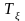 қиғаш сызықтағы сыңарлары элементарлы
кесіндінің салыстырмалы ұзаруы жылдамдығы
болып саналады. Осы салыстырмалы ұзару
жылдамдығы координатты оське параллельді
болады.
қиғаш сызықтағы сыңарлары элементарлы
кесіндінің салыстырмалы ұзаруы жылдамдығы
болып саналады. Осы салыстырмалы ұзару
жылдамдығы координатты оське параллельді
болады.
Тензордың бұйірдегі сыңарларын тік бұрышты кесінділердің бұрылу жылдамдығы немесе ығысу деформациясының жылдамдығы деп атайды.
Басты деформация жылдамдығы. Симметриялы деформация жылдамдығы тензорын координатты осьтерді бұру арқылы мынандай диагональды түрге келтіруге болады:
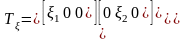 .
(8.9)
.
(8.9)
Деформация жылдамдығының бас сыңарлары мынандай теңсіздікті қанағаттандырады: ξ1 ≥ ξ2 ≥ ξ3.
Жаңа
координатты жүйеде тензордың бұйірдегі
сыңарлары нөльге тең болады, яғни нөльден
айырмашылықта тек координатты осьтер
бағытындағы сызықты деформация
жылдамдықтары болады. Басқаша айытқанда
жаңа координатты осьте тензордың ығысу
деформациясы жылдамдықтары нөльге тең
болады. Осындайда, координатты
жазықтықтарға параллельді қырлары
(биіктігі dl)
және
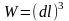 көлемі бар элементарлы куб dt
уақытысында қырлары dl(1
+ ξi)dt
және көлемі ω болатын тікбұрышты
параллелепипедке айналады. Осындайда,
тым жоғары реттікті шексіз кішкентайға
дейінгі дәлдікпен көлемнің салыстырмалы
өзгеруі мынаған тең:
көлемі бар элементарлы куб dt
уақытысында қырлары dl(1
+ ξi)dt
және көлемі ω болатын тікбұрышты
параллелепипедке айналады. Осындайда,
тым жоғары реттікті шексіз кішкентайға
дейінгі дәлдікпен көлемнің салыстырмалы
өзгеруі мынаған тең:
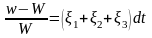 .
.
Деформация
жылдамдығының бас сыңарлары мынандай
кубтық теңдеудің нақты түбірлері болады:
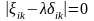 немесе жайылған түрде жазған кезде
немесе жайылған түрде жазған кезде
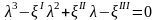 .
(8.10)
.
(8.10)
Деформация жылдамдығы тензорының инвариантары мынаған тең:
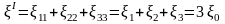 ;
(8.11)
;
(8.11)
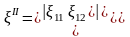 ;
(8.12)
;
(8.12)
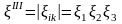 .
(8.13)
.
(8.13)
Бірінші инвариантың физикалық мағанасы бар. Бұл мағана бойынша бірінші инвариант көлемнің салыстырмалы өзгеруінің жылдамдығына тең. Осы физикалық мағана мынандай теңдіктен де шығады: