
- •Глава 4 Основы теории обнаружения сигналов на фоне шумов
- •Помехи в каналах радиотехнических систем. Совместное прохождение сигнала и шума через тракт приемника
- •Основная терминология теории статистических решений
- •Статистическая теория обнаружения сигнала на фоне помех (шумов).
- •4.3.1. Двухальтернативная задача обнаружения сигналов.
- •Ошибки при решении задачи обнаружения сигнала.
- •4.4 Критерии оптимального обнаружения сигналов на фоне помех (шумов)
- •4.4.1. Критерий идеального наблюдателя (критерий Котельникова – Зигерта).
- •4.4.2. Критерий Неймана – Пирсона.
- •4.4.3. Критерий Вальда–Вольфовича.
4.3.1. Двухальтернативная задача обнаружения сигналов.
Рассмотрим случай, когда сигнал принимает одно из двух возможных значений (1 или 0). В этом случае принятое колебание можно записать в виде
|
(4.15) |
Если
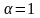 - сигнал есть, а при
- сигнал есть, а при
 - сигнала нет (только шум).
- сигнала нет (только шум).
Наличие
шума
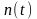 делает
Y(t)
случайной величиной. Приемник должен
оптимальным образом определить, чему
равно
делает
Y(t)
случайной величиной. Приемник должен
оптимальным образом определить, чему
равно
 .
.
Если S(t) носит дискретный характер, то нужно знать распределение вероятности P(S/Y).
Если сигнал непрерывный, то нужно знать его плотность вероятности (S/Y).
Понятно, что и P(S/Y) и (S/Y) можно получить только в результате опыта, поэтому эти распределения вероятностей называют апостериорными.
Нас в дальнейшем будут интересовать дискретные сигналы. В этом случае формула (4.15) примет вид
|
(4.16) |
|
(4.17) |
|
|
Апостериорная вероятность P(SUш/Y) будет определяться условной вероятностью того, что в реализации Y(t) сигнал есть.
Апостериорная вероятность P(Uш/Y) будет определяться условной вероятностью того, что в реализации Y(t) только шум.
Таким образом, приемник имеет дело с двумя гипотезами:
-
сигнал есть
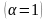 ,
апостериорная вероятность такого
события P(SUш/Y)
является условной вероятностью того,
что Y
состоит из сигнала и шума;
,
апостериорная вероятность такого
события P(SUш/Y)
является условной вероятностью того,
что Y
состоит из сигнала и шума;
-
сигнала нет
 ,
апостериорная вероятность такого
события P(Uш/Y)
является условной вероятностью, что
принят только шум.
,
апостериорная вероятность такого
события P(Uш/Y)
является условной вероятностью, что
принят только шум.
Как видно, здесь одна гипотеза исключает другую, т.е. они несовместимы, поэтому такую задачу обнаружения называют двухальтернативной.
Анализируя P(SUш/Y) и P(Uш/Y) по определенному правилу, приемник может принять одну из гипотез
|
(4.18) |
 -
сигнал есть;
-
сигнал есть;
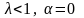 -
только шум.
-
только шум.
Но
P(SUш/Y)
и P(Uш/Y)
есть условные вероятностные характеристики,
а
 - это их отношение. Отсюда могут возникнуть
ошибки двух родов.
- это их отношение. Отсюда могут возникнуть
ошибки двух родов.

Рис. 4.9
На выходе детектора приемника сигнал имеет вид, показанный на рис. 4.9.
Ошибки при решении задачи обнаружения сигнала.
Итак, возникают ошибки двух родов:
- ошибка первого рода - ложная тревога. Она оценивается условной вероятностью
|
(4.19) |
- ошибка второго рода - пропуск цели. Она оценивается условной вероятностью
|
(4.20) |
Ошибки
PЛТ
и
РПЦ
зависят от отношения сигнал/шум по
энергии и выражаются величиной
 .
Кроме того, они зависят от порога
регистрации VПОР
(рис.
4.5).
.
Кроме того, они зависят от порога
регистрации VПОР
(рис.
4.5).
Полная вероятность ошибки равна
|
(4.21) |
Где Р(Uш) - априорная вероятность шума (вероятность правильного обнаружения шума); Р(SUш) - априорная вероятность сигнала и шума; Р(SUш/Uш) и Р(Uш/SUш) - это апостериорные условные вероятности соответственно того, что в принятой реализации есть сигнал или только шум.
Никакие приборы не могут определить условные вероятности Р(SUш/Uш) и Р(Uш/SUш), входящие в выражение (4.21). Эти условные вероятности принято записывать в виде P(SUш/Y) и P(Uш/Y).
Для того чтобы вычислить вероятность ошибки, нужно знать априорные вероятности Р(SUш) и Р(Uш), а так же обратные вероятности:
P(Y/SUш)
-
вероятность того, что принимаемая
реализация
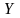 образована сигналом и шумом;
образована сигналом и шумом;
P(Y/Uш) - вероятность того, что реализация образована только шумом.
Эти обратные вероятности были получены Байесом и называются функциями правдоподобия.
Отношение функций правдоподобия называется коэффициентом правдоподобия
|
(4.22) |
Согласно формуле Байеса
|
(4.23) |
|
(4.24) |
Здесь Y – это одна и та же реализация принятая приемником, которая может содержать сигнал и шум или только шум.
Подставляя в выражение (4.18) полученные условные вероятности, по формуле Байеса найдем решение, которое позволит с определенной вероятностью принять одну из гипотез - есть сигнал в принятой реализации Y сигнал или его нет.
Формула принятия решения на основе (4.18) имеет вид
|
(4.25) |
Таким образом
|
(4.26) |
|
|
Априорные
вероятности
Р(SUш)
и
Р(Uш)
известны
заранее. Следовательно, дело в выборе
порога VПОР
который в свою очередь влияет на L.
Величину VПОР
выбирают исходя из знания априорных
вероятностей
 и
и
 ,
т.е.
,
т.е.
|
(4.27) |
|
|
Таким образом, операция принятия решения сводится к неравенству
. |
(4.28) |
При условии, что PЛТ и РПЦ одинаково нежелательны, решение сводится к следующему
- - сигнал есть;
- сигнал есть;
- - в принятой реализации только шум.
- в принятой реализации только шум.
Принятие решения в случае приема случайных сигналов с неизвестными параметрами ставят вероятности PЛТ и РПЦ в совершенно неоднозначную ситуацию.
Так, например, в радиолокации случайными параметрами могут быть дальность до объекта, его координаты, доплеровский сдвиг частот и т.п.
Вероятности
PЛТ
и
РПЦ
существенно
неравнозначны и зависят от конкретной
ситуации, ибо принятие решения ведет к
определенным серьезным последствиям.
Поэтому в формулу принятия решения в
данном случае вносится некоторая
величина
 ,
которая называется ценой
решения.
Это особенно важно в радиолокации.
,
которая называется ценой
решения.
Это особенно важно в радиолокации.
Сама же формула принятия решения в этом случае принимает вид
|
(4.29) |
Итак, если - сигнал есть; если - только шум; а в случае L = 1 - это критерий идеального наблюдателя, который рассматривается в параграфе 4.3. Таким образом, величина L показывает, какая из гипотез наиболее правдоподобна.

 .
. ;
; .
. ,
, ;
; .
. ,
, .
.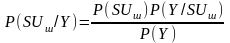 ;
; .
.
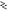 1.
1. 1.
1. .
. .
.