21

Глава 4 Основы теории обнаружения сигналов на фоне шумов

1. Помехи в каналах радиотехнических систем. Совместное прохождение сигнала и шума через тракт приемника

Обнаружение называется процесс принятия решения о наличии или отсутствии цели в каждом элементарном разрешаемом объеме РЛС. Трудность обнаружения возникает в тех случаях, когда сигналы принимаются в присутствии помех. В каналах радиотехнических систем действуют флуктуационные, импульсные и сосредоточенные помехи. Наибольший интерес представляет собой флуктуационная помеха, поскольку она имеет место во всех каналах радиотехнических систем. Борьба с флуктуационной помехой является одной из главных задач обеспечения помехоустойчивости любой радиотехнической системы. Флуктуационная помеха близка по структуре к “белому” шуму, относится к сплошным помехам с бесконечным спектром и равномерной спектральной мощностью 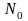. На практике белый шум по спектр ограничен полосой пропускания приемника. Таким образом, флуктуационная помеха это случайный процесс, структура которого описывается одномерной плотностью вероятности стационарного случайного процесса, т.е. имеет нормальное (Гауссовское) распределение вида

,

(4.1)

где 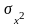- дисперсия (при 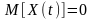– мощность флуктуационной помехи). Характеризует степень разброса величины относительно среднего;

Х - флуктуация случайного процесса (флуктуационной помехи);

- математическое ожидание (среднее значение) случайного процесса (флуктуационной помехи). Определяет максимум распределения, наиболее вероятное значение величины случайного процесса (флуктуационной помехи).

Смысл нормального распределения становится понятен из его формы. Наиболее вероятные значения случайной величины расположены вблизи его пика (среднего). По мере удаления от него, вероятность значений уменьшается и если значение расположено в «хвосте» распределения, то оно очень маловероятно. Типичные формы нормального распределения для различных средних и дисперсии представлены на рис. 4.1.

Рис. 4.1

Плотность вероятности Р(Х) уменьшается с увеличением значений Х, а график плотности вероятности нормального распределения симметричен относительно нуля (рис. 4.1,а).

Рис. 4.1

Если 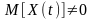, то кривая Р(Х) сместится вправо, как это показано на (рис. 4.1,б), но нормальное распределение останется неизменным.

Задачей статистической теории радиотехнических систем является прием сигналов на фоне шумов. Понятно, что при появлении сигнала математическое ожидание случайного процесса уже не будет равно нулю, а будет зависеть от величины отношения энергии сигнала к спектральной плотности шума.

Зная распределения плотностей вероятностей Р(Х) на входе приемника при наличии и отсутствии сигнала, можно найти статистические характеристики флуктуационной помехи заменив Р(Х) на P(U_ш)

Математическое ожидание для шума можно

,

(4.2)

а для сигнала и шума

.

(4.3)

Отличие математического ожидания М_СШ от нуля говорит о том, что в принимаемом сигнале на входе приемника присутствует информационный или случайный сигнал.

Рис. 4.2

Дисперсия при находится по формуле

.

(4.4)

Если на вход детектора Д поступает шум 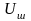, то на его выходе приемника будет получена огибающая этого шума (рис. 4.2,а).

На выходе приемника плотность вероятности огибающей шума описывается законом Релея (рис. 4.2,б)

,

(4.5)

где - это математическое ожидание огибающей шума на выходе приемника (рис. 4.3)

При наличии только шума, отношение сигнал/шум на выходе приемника равно

,

(4.6)

где N₀ – спектральная плотность шума;

Е_С – энергия сигнала.

Рис. 4.3

Рассмотрим, что произойдет с плотностью вероятности на выходе приемника при наличии сигнала. Уже отмечалось, что сигнал на входе приемника смещает вправо гауссовскую кривую (рис. 4.1.б). Величина смещения кривой на выходе приемника (рис. 4.3) определяется энергией сигнала Е_с, т.е. чем больше отношение сигнал/шум, тем больше кривая распределения плотности вероятности смещается вправо и приближается к нормальному закону распределения. При отношении сигнал/шум равным пяти, кривая P(V_СШ) описывается нормальным законом распределения плотности вероятности.

Очевидно, что при некоторых отношениях сигнал/шум кривые и пересекаются (рис. 4.3). Это значит, что при определенном пороге регистрации шум может быть принят за сигнал, или сигнал окажется ниже порога и будет пропущен.

Для разных значений , семейство кривых распределения плотности вероятности P(V_СШ) показано на рис. 4.4. Эти кривые описываются обобщенным законом Релея или законом Райса

,

(4.7)

где 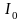- модифицированная функция Бесселя нулевого порядка (табличное значение).

Рис. 4.4

Закон Райса играет фундаментальную роль при обнаружении сигнала на фоне шума.

При выбранном пороге V_ПОР регистрации сигнала (рис. 4.5) возможны ошибки двух родов:

- вероятность ложной тревоги - Р_ЛТ;

- вероятность пропуска цели - Р_ПЦ.

Поскольку кривые распределения плотности вероятности шума и сигнала и шума пересекаются, а регистрация сигнала обычно ведется по установленному порогу V_ПОР, то всегда могут возникнуть ситуации, когда сигнал есть, но он окажется ниже порога. Это случай пропуска цели Р_ПЦ.

В свою очередь, при отсутствии сигнала, шум может превзойти установленный порог. Это случай ложной тревоги Р_ЛТ.

Практическая ценность закона Райса состоит в следующем:

- он позволяет определить оптимальное значение V_ПОР в приемнике и ослабить действие шума;

- он дает возможность вычислить вероятность превышения этого порога шумом, т.е. определить Р_ЛТ, или найти вероятность того, что сигнал окажется ниже V_ПОР, т.е определить Р_ПЦ.

Рис. 4.5

Увеличение 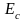всегда желательно, т.к. кривая распределения сигнал/шум смещается вправо (рис. 4.5), и притом же пороге V_ПОР уменьшается вероятность пропуска цели Р_ПЦ. Кроме того, увеличивая V_ПОР можно уменьшить вероятность ложной тревоги Р_ЛТ.

К роме вероятностей Р_ЛТ и Р_ПЦ существует еще вероятность правильного обнаружения D. Эта вероятность так же как Р_ЛТ и Р_ПЦ зависит от величины , т.е. от отношения сигнал/шум на выходе приемника, и рассчитывается при Р_ЛТ = const.

Зависимость D от q при заданной Р_ЛТ называется характеристиками обнаружения (рис. 4.6.). Они позволяют при заданной q_min определить D для фиксированного значения Р_ЛТ, и, наоборот. При этом Р_ЛТ имеет порядок 10^-1 – 10^-5.

Р ассмотрение чисто гипотетической ситуации – обнаружение сигнала с полностью известными параметрами – позволяет оценить теоретический предел улучшения характеристик обнаружения. При обнаружении указанного сигнала неизвестным является сам факт наличия или отсутствия сигнала.

При обнаружении одиночного сигнала с полностью известными параметрами, характеристики обнаружения могут быть оценины с помощью приближенной формулы

. (4.8)

На рис. 4.7 представлены характеристики обнаружения с полностью известными параметрами.

Если производиться обнаружение не одного, а N_c одинаковых сигналов, то суммарное отношение сигнал/шум на входе приемника возрастет в N_c раз и будет иметь выражение

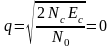
При приеме одиночного сигнала со случайной начальной фазой характеристики обнаружения описываются следующей приблизительной формулой

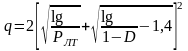. (4.9)

Если принимается последовательность Nc импульсных сигналов со случайной начальной фазой, то на характеристику обнаружения существенно влияет наличие взаимосвязи фаз отдельных сигналов. Пачку импульсных сигналов называют когерентной, если в пределах всей пачки имеет место определенная зависимость фазы колебаний от времени. Характеристики обнаружения когерентной пачки импульсов со случайной начальной фазой определяются соотношением (4.9) .

Пачку импульсов называют некогерентной в том случае, если начальные фазы отдельных сигналов статистически независимы. После системы обработки результирующее отношение сигнал/шум некогерентной пачки импульсов оказывается меньшим, чем у когерентной (при одинаковой суммарной энергии сигналов на входе приемника). Для Nc>>1 характеристики обнаружения сигналов с неизвестной начальной фазой могут быть определены с помощью приближенной формулы

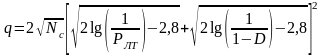(4.10)

Если закон распределения начальной фазы сигнала равномерный в пределах от 0 до 2, а распределение амплитуд подчинено закону Релея, тогда характеристики обнаружения можно найти следующим образом

. (4.11)

При обнаружении пачки Nc некогерентных импульсов с флуктуирующими начальной фазой и амплитудой при Nc>>1 праведлива приближенная формула

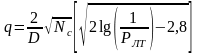. (4.12)

В большинстве элементов приемного тракта имеет место уменьшение отношения сигнал/шум на выходе по сравнению с его значением на входе. Это уменьшение отношения сигнал/шум принято называть потерями при обработке d_i. Потери выражаются либо в разах, либо в децибелах.

Если в приемнике имеется n элементов с потерями, то суммарные потери тракта равны

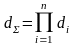. (4.13)

Для того чтобы обеспечить обнаружение сигналов с заданными вероятностями D и Р_ЛТ, при использовании реального приемника следует иметь на входе отношение сигнал/шум в Σ a раз больше значения q, определяемого по одной из формул (4.8), (4.9), (4.10), (4.11), (4.12) или по графику на рис. 4.7.

Ниже перечислены основные виды потерь:

а) потери d_а в антенне, возникающие вследствие изменения амплитуды принимаемых сигналов при сканировании антенны. В среднем можно принять d_а 1,5;

б) потери d_вч в высокочастотном тракте, вызываемые затуханием энергии сигналов в фидерах и антенных коммутаторах. В среднем d_вч 1,6;

в) потери d_дет в детекторе зависят от отношения сигнал/шум и количества накапливаемых импульсов. При приближенных расчетах используют усредненную характеристику потерь в детекторе в соответствии с рис. 4.8;

Рис. 4.8.

г) потери d_ко , вызванные заменой оптимального фильтра в приемнике квазиоптимальным, согласованным только по полосе пропускания. Значения коэффициента d_ко приведены в таблице 4.1, где f_ф – полоса пропускания фильтра по половинной мощности, τ – длительность импульса по половине максимального значения напряжения;

д) потери оператора d_оп, связанные с тем, что для фиксации оператором отметки цели на индикаторе должно иметь место некоторое превышение яркости отметки над шумовым фоном. В среднем можно принять d_оп 1,5;

Таблица 4.1.

Радиоимпульс	Фильтр	fфτ	dко
Прямоугольный	Идеально прямоугольный	1,37	1,21
Прямоугольный	Гауссов	0,72	1,26
Гауссов	Гауссов	0,44	1
Прямоугольный	Одиночный резонансный контур	0,4	1,24
Прямоугольный	Два резонансных контура	0,613	1,14
Прямоугольный	Пять резонансных контуров	0,672	1,12

е) потери d_ас при автоматическом съеме данных, объясняющиеся тем, что отсчет выходного напряжения производится не в тот момент, когда сигнальная составляющая достигает своего максимума. Можно считать, что d_ас = 2.

При решении ряда практических задач полезно использовать коэффициент различимости k_р, представляющий собой отношение энергии Ec одного импульсного сигнала к спектральной плотности N₀ шума при условии обнаружения пачки из Nc с вероятностями D и Р_ЛТ:

, (4.14)

где q определяется по одной из формул (4.8), (4.9), (4.11), либо по графику на рис. 1, как если бы принимался один сигнал.
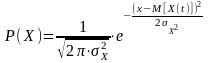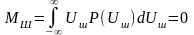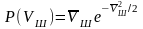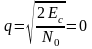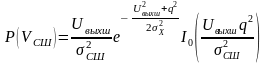