Представление лф в базисе Шеффера с ограничениями на число входов логических элементов
Для представления ЛФ в базисе Шеффера (элементы И-НЕ) она минимизируется (осуществляется склейка единиц в картах Карно) и берется двойная инверсия полученной минимальной ДНФ. Инверсия ДНФ раскрывается по правилу де Моргана, и сумма преобразуется в произведение инверсных значений слагаемых. Ограничение на число входов ЛЭ определяет ограничение на число слагаемых в ДНФ под знаком инверсии, поэтому двойную инверсию не следует применять к суммам с числом слагаемых, превышающим максимальное число входов используемых для реализации ЛЭ. В этом случае задача может быть решена двумя путями.
Первый путь – формальный. Исходная минимальная ДНФ ЛФ рассматривается как сумма сумм. Двойные инверсии берутся над группами слагаемых, число которых не превышает заданного ограничениями значения. Двойные инверсии берутся также над суммами групп. Такой подход наиболее прост, но его использование приводит к появлению дополнительных инверторов в схеме и часто не позволяет получить наиболее экономичную схему.
Второй путь - факторизация (выделение общих фрагментов) логического выражения, заданного в ДНФ. Слагаемые минимальной ДНФ разбиваются на группы, имеющие общие сомножители, которые выносятся за скобки. Полученная в каждой группе сумма также может быть факторизована. Факторизацию целесообразно закончить, когда не осталось сумм с числом слагаемых, превышающим заданные ограничения. Перевод каждой суммы (общей и по группам) в базис И-НЕ осуществляется известным способом. Различная группировка исходных слагаемых минимальной ДНФ приводит к различным логическим структурам, отличающимся и быстродействием, и аппаратурными затратами.
Построение кс по логическому выражению
Для построения КС логическое выражение должно быть записано в требуемом базисе. Далее осуществляется определение глубины вложенности функций Шеффера. Для этого в логическом выражении последовательно по ступеням выполнения, начиная от выхода к входам, нумеруются функции Шеффера (например, проставляется номер возле соответствующей инверсии). Функции Шеффера, значение которой определяет значение искомой функции, присваивается номер 1. Функциям, определяющим аргументы функции первого уровня, присваивается номер 2 и т.д., пока входные переменные функций не будут задаваться только исходными аргументами. Количество уровней определяет "ширину" схемы, максимальное количество элементов в каком-либо уровне определяет "высоту" схемы.
Собственно построение КС начинается с ориентировочного определения мест расположения ЛЭ. Лист по ширине разбивается на вертикальные столбцы, в каждом из которых располагаются ЛЭ одного уровня. Схема рисуется, начиная с ЛЭ первого уровня (справа налево). В левой части рисунка предусматривается область для размещения инверторов и шин входных переменных.
Пример синтеза комбинационной схемы
Набор используемых в примере элементов представлен на .
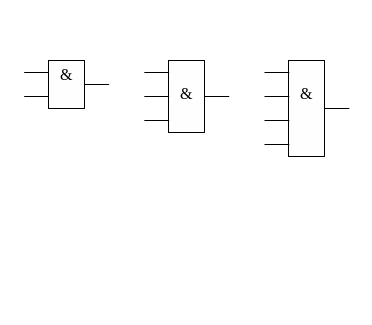
Рис.2.2. Используемые при синтезе элементы и разводка их выводов.
Пусть требуется синтезировать схему, реализующую логическую функцию от пяти аргументов: y = f(x5, x4 ,x3 ,x2 ,x1). Функция не полностью определена и задана в списочной форме:
F1=(0,2,5,6,8-10,13,15,17,19-21,25,28);
Fн=(12,23,29,30).
Построим таблицу истинности, предусмотрев в ней дополнительные графы yтеор. и yэксп.
Графа yисх. соответствует заданной ЛФ. Графа yтеор. заполняется после доопределения функции в процессе минимизации. Графа yэксп. заполняется по результатам эксперимента.
Номер набора |
x5 |
x4 |
x3 |
x2 |
x1 |
yисх |
yтеор |
yэксп |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
2 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
3 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
6 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
8 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
10 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
11 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
12 |
0 |
1 |
1 |
0 |
0 |
н |
0 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
14 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
15 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
16 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
17 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
18 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
19 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
20 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
22 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
23 |
1 |
0 |
1 |
1 |
1 |
н |
1 |
|
24 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
25 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
26 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
27 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
28 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
29 |
1 |
1 |
1 |
0 |
1 |
н |
1 |
|
30 |
1 |
1 |
1 |
1 |
0 |
н |
0 |
|
31 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
Построим карту Карно (2.3) и произведем склеивание в соответствии с методикой, изложенной в подразделе 1.1.3.
Единицы, помеченные
точкой (1
),
имеют единственный вариант склеивания
(охватывающий максимальное количество
единиц) и эти склейки составляют ядро
функции (склейки 1...5). Неопределенности,
охваченные склейками, доопределяются
единицами, неохваченные - нулями, и
заполняем графу yтеор.
в таблице истинности.
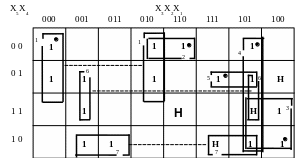
Рис.2.3. Пример построения карты Карно.
По результатам склеивания запишем ЛФ в минимальной ДНФ:
.
Выполним факторизацию логического выражения (вынесение за скобки) и переход к базису Шеффера с ограничениями (ЛЭ 2И-НЕ, 3И-НЕ, 4И-НЕ):
Пометив уровни вложенности функций Шеффера в логическом выражении, строим в графическом редакторе принципиальную схему, которая приведена на Error: Reference source not found2.11.