2.6 Дополнительные сведения из теории переключательных функций.
- не полностью определенные переключательные функции
- скобочные формы
- переход к универсальным базисам
Не полностью определенные ПФ
Не полностью определенной называется ПФ из n аргументов, значения которых определены не на всех 2n аргументах
Т.е наборы, на которых он не определена, называются запрещенными. Соответственно набору запрещено соответствие или ему запрещено появление.
Запрещенный набор обладает теми свойствами, что не может появиться на входе устройства реализующего данную ПФ.
Запрещенные наборы могут быть использованы при синтезе устройства, реализующего ПФ
Пример:
x4 |
x3 |
x2 |
x1 |
f |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
- |
0 |
1 |
0 |
1 |
- |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
- |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Минимизация конъюнктивных нормальных форм
Цель: построение минимальной КНФ.
2 способа:
1. Реализовать минимизацию ДНФ, а потом каким-либо способом (через формулы де Моргана) перейти к КНФ.
2. Непосредственная минимизация КНФ (по способу зеркально аналогичному минимизации ДНФ).
На картах Карно:
Контуры, охватывающие 0.
В записи дизъюнкций инвертируют аргументы
Скобочные формы.
Общего
метода минимизации скобочных форм нет.
(Бинарные программы (алгоритмы), два типа: условный переход и присвоение).
Запись и минимизация в неканонических базисах.
В не избыточных базисах невозможна минимизация.
Переход к неканоническому базисы: стрелка пирса, штрих Шеффера.
Есть способ через минимальную КНФ и минимальную ДНФ.
Полином Жегалкина
X3 |
X2 |
X1 |
g |
F |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
Порождающая матрица:
Каждый элемент в случае 1 заменить порождающей матрицей, а случае 0:
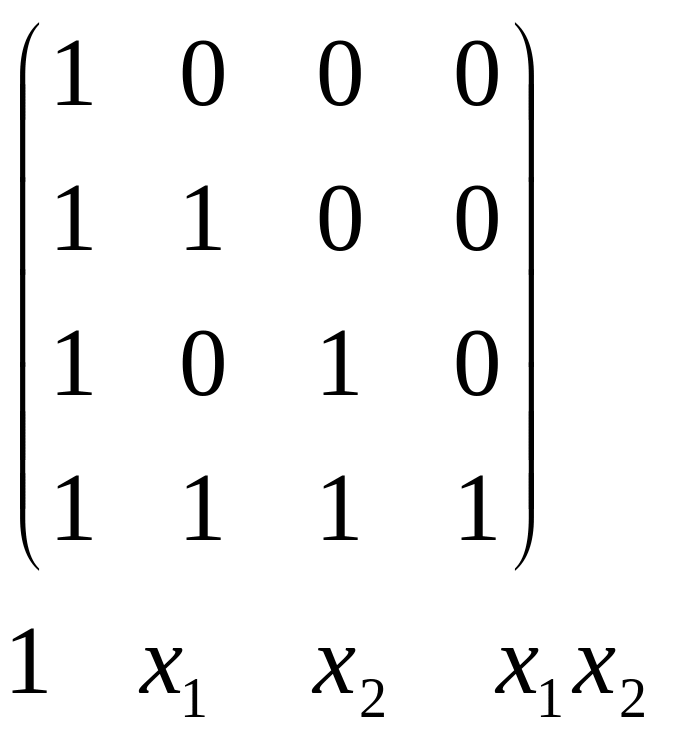
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
x1 |
x2 |
x1x2 |
x3 |
x1x3 |
x2x3 |
x1x2x3 |