Логические основы цифровой вычислительной техники 2.1 Физическое представление информации в ЦВМ. Понятие об элементах структуры ЦВМ.

Существует три способа физического представления символов алфавита в ЦВМ:

1. потенциальный

2. импульсный

3. динамический

два состояния 1 и 0, да и нет, нет и да

Для ЦВМ характерна не только дискретность сигналов, но и дискретность моментов времени, в которые они рассматриваются. Интервал между соседними дискретными моментами времени называется такт.

3 типа элементов:

логические

запоминающие

вспомогательные

Теория автоматов.

Назовем устройство, осуществляющее преобразование дискретной информации входной в выходную – АВТОМАТ.

2 случая функционирования автоматов:

1. Информация на выходе А в каждый момент времени определяется лишь комбинацией значений входных переменных. Автоматы без памяти или комбинационные автоматы (схемы).

Y=(X)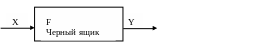

X = {x₁,x₂,…,x_n}

Y = {y₁,y₂,…y_n}

2. Входная информация определяется ещё и предысторией автомата. Автомат с памятью.

В практической вычислительной технике автоматы с памятью рассматриваются как конечные автоматы (т. е. число состояний устройства конечно).

Самое абстрактное описание F:

ВС – вспомогательные элементы.

КС – комбинационная схема.

ДЭ – дополнительные элементы.

2.2 Переключательные функции: определение и основные понятия.

Будем называть переключательной функцией функцию следующего вида:

причем:

если (обозначает зависимость функции от каждой переменной)

( )

Все переменные и сама f определены на .

Синонимы: булева функция, логическая функция, функция алгебры логики.

В отличие от непрерывной функции переключательная функция определена на конечном наборе значений аргументов, сама принимает конечное число значений и в самом простом случае может быть задана таблично.

Общий вид таблицы:

X1	X2	…	Xn-1	Xn	f
0	0	…	0	0	F(0,0..,0)
0	0	…	0	1	F(0,0,...,1)
…	…	…	…	…	…
0	0	…	1	0	F(0,0,…,1,0)

Код Грея.

Такая таблица (таблица истинности) полностью описывает переключательную функцию.

Таблица истинности избыточна, мы можем, например, усечь таблицу, исключив строки с нулевым результатом. Усечение таблицы истинности.

Мы можем добавить столбец для описания функции от тех же аргументов, например

n – столбцов для аргументов

m – столбцов для функций

Количество функций от n аргументов равняется

- две переключательные функции могут оказаться равными, если они принимают одни и те же значения при одном и том же наборе аргументов.

1. Переключательная функция называется существенно зависимой от аргумента x_i, если

2. Если же от аргумента функция x_i существенно не зависит, то аргумент называется фиктивным.

Количество аргументов существенно зависящих от n определяется следующей рекурсивной формулой:

2.3 Элементарные логические функции. Система логических функций.

Элементарные логические функции – функции существенно зависящие от одного или двух аргументов.

1 аргумент:

X	1	0	x	⌐x
0	1	0	0	1
1	1	0	1	0

x1	x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
		Пустое множество	↓ Стрелка Пирса	Обратные импликации		Обратные импликации		Исключающее или	Штрих Шевффера	Конъюнкция	Функция равнозначности ~		Импликация →		Импликация ←	Дизъюнкция	1

f₀ и f₁₅ фиктивно зависит от x₁ и x₂; f₀ = 0 f₁₅ = 1

f1= f2= f3= f4= f5= f6= f7=

f8= f9= f10= f11= f12= f13= f14=

Условимся называть некий набор элементарных переключательных функций, используемых для записи выражений, соответствующих более сложных переключательных функций – базисом.

Полным базисом (системой) переключательной функции называют такую совокупность элементов ПФ, с помощью которой путем подстановки и суперпозиции может быть любая ПФ любого конечного числа аргументов.

Полные базисы:

Первый базис избыточен, это неплохо, так как может упрощать синтез выражений.

Тьюринг, Пост.

Замкнутый класс логических функций – функции, обладающие свойствами замкнутого класса, через них можно выразить только функции того же класса.

5 замкнутых классов – особенные.

1. Сохраняющие константу 0.

2. Сохраняющие константу 1.

3. Самодвойственные

4. Монотонные (возрастающие).

5. «Линейные».

Теорема о функциональной полноте базиса. Теорема Поста и Яблонского.

Для того что система элементов ПФ была функционально полной, необходимо и достаточно, чтобы она включала в себя элементарные функции (хотя бы по одной), не принадлежащие к 5 замкнутым классам.

1.

f(0,0,…,0) = 0

2. f(1,1,…1) = 1

3.

4. Монотонность

x_i =1

x_j = 0

x_i>x_j

x_j = 0 x_i =0 x_i=x_j

x_j = 1 x_i =1 x_i=x_j

Определение монотонности

Функция называется монотонной, если

При условиях

И так на всем наборе из всех 2ⁿ аргументов

5. Свойство «линейности»

попадают между 0,1,

	0	1	Самодвойств.	Монотонность	Линейность
	+	+	-	+	-
	+	+	-	+	-
~	-	-	+	-	+
	+	-	-	-	+
1	-

Базис Жегалкина:

Стрелка Пирса:

-

-

-

-

-

Булева:

Жегалкина:

Алгебра Гильберта:

Алгебра Новикова: