3. Расчет дополнительных перемещений оси шпинделя, вызванных податливостью опор
Обозначим
упругое перемещение опоры A,
а через
- упругое перемещение опоры B
(рис.2.21).
Рис.2.21. Схема для расчета упругих перемещений опор шпинделя
Запишем выражения для определения дополнительного перемещения оси шпинделя yоп и дополнительного угла наклона оп с учетом податливости опор:
;
(2.120)
. (2.121)
Приближенное значение полного упругого перемещения опоры можно определить по формуле
, (2.122)
где e - податливость опоры; K - коэффициент, учитывающий характер посадки подшипника в опоре (K = 1, если подшипник установлен с натягом; K = 2, если подшипник установлен с зазором); R - реакция в опоре.
Податливость опоры e является величиной, обратной жесткости подшипника j
. (2.123)
Формула (2.123) справедлива для случая, когда в опоре установлен один подшипник. Если в одной опоре установлено несколько подшипников, то общая податливость опоры определяется по формуле
. (2.124)
На рис.2.22 представлены графики зависимости радиальной жесткости j подшипника от его внутреннего диаметра для наиболее распространенных типов шпиндельных подшипников качения [16].
С
высокой степенью приближения данные
графики могут быть описаны функциональными
зависимостями вида
:
а) для подшипников типа 3182100
; (2.125)
б) для подшипников типа 2007100
; (2.126)
в) для подшипников типов 46200, 46100
. (2.127)
Рис.2.22. Зависимость радиальной жесткости подшипника от его внутреннего диаметра
4. Расчет перемещений оси шпинделя, вызванных наличием реактивного момента в передней опоре
Если в передней опоре расположено несколько рядов тел качения, то при изгибе шпинделя в опоре создается реактивный (защемляющий) момент Mр, направленный противоположно моменту нагрузки. В расчетах, для определения реактивного момента пользуются линейной зависимостью
,
(2.128)
где Mн - момент нагрузки, действующий в передней опоре, определяется по формуле
;
(2.129)
-
коэффициент, зависящий от типа и
количества подшипников, расположенных
в передней опоре, значения приводятся
в табл.2.16.
Расчетная схема для определения перемещений, вызванных наличием реактивного момента приводится на рис.2.23. Расчет деформаций шпинделя выполняется аналогично п.п. 1 – 3, рассмотренным выше.
Таблица 2.16.
Значения коэффициента защемления
-
Подшипники, установленные в передней опоре
Коэффициент защемления
0,45...0,65
0,30...0,45
0,30...0,45
0,20...0,30
0,10...0,20
0,10...0,20
4.1. Определение опорных реакций от действия реактивного момента в передней опоре
Уравнение моментов относительно опоры A (см. рис.2.23)
;
,
откуда
. (2.130)
Уравнение проекций сил на ось y
;
,
откуда
. (2.131)
y
RB
RA
Mr
x
B
A
IV
III
II
I
Рис.2.23. Расчетная схема для определения угловых и линейных перемещений оси шпинделя, вызванных наличием реактивного момента
4.2. Определение перемещений оси шпинделя без учета упругости опор от действия реактивного момента в передней опоре
Составим дифференциальные уравнения изогнутой оси для каждого участка и проинтегрируем их.
Первый
участок (
):
;
; (2.132)
. (2.133)
Второй
участок (
):
;
; (2.134)
. (2.135)
Третий
участок (
):
;
; (2.136)
. (2.137)
Четвертый
участок (
):
;
; (2.138)
. (2.139)
Составляем
уравнения для определения постоянных
интегрирования
.
При
.
При
При
При
Решив эти уравнения, можно определить постоянные интегрирования , входящие в формулы (2.132) - (2.139), которые позволяют определить угловые и линейные перемещения оси шпинделя, вызванные реактивным моментом в передней опоре, без учета упругости опор (соответственно шп.р = y' и yшп.р).
4.3. Расчет дополнительных перемещений оси шпинделя, вызванных податливостью опор от действия реактивного момента в передней опоре шпинделя
Упругие перемещения опор шпинделя вычисляются по формуле (2.122), а дополнительное перемещение оси шпинделя yоп.р и дополнительный угол наклона оп.р – по формулам (2.120) и (2.121).
5. Определение суммарных значений перемещений оси шпинделя в одной плоскости
Суммарные значения угла наклона и перемещения оси шпинделя с учетом податливости его опор и с учетом реактивного момента, действующего в передней опоре, в одной плоскости определяются по формулам
(2.140)
Компоненты которых определяются по методике, описанной выше.
6. Расчет результирующих значений перемещений оси шпинделя
Как уже указывалось, расчет перемещений оси шпинделя необходимо производить в двух плоскостях (ZX и YX). В каждой плоскости определяются деформации в требуемых сечениях. Затем находятся результирующие величины:
; (2.141)
. (2.142)
Полученные
значения сравниваются с допустимыми
для данного сечения
и
.
Конструктивные схемы 2 и 3.
y
x
P5
RB
RA
P3
M3
M5
B
A
V
IV
III
II
I
Рис.2.24. Расчетная схема для определения угловых и линейных перемещений оси шпинделя
1. Определение опорных реакций
Уравнение моментов относительно опоры A (рис.2.24)
;
,
откуда
. (2.143)
Уравнение проекций сил на ось y
; ,
откуда
. (2.144)
2. Определение линейного и углового перемещений оси шпинделя без учета упругости опор
Составляем дифференциальные уравнения изогнутой оси для каждого участка в соответствии с рис.2.24 и интегрируем их.
Первый
участок (
):
;
; (2.145)
. (2.146)
Второй
участок (
):
;
; (2.147)
. (2.148)
Третий
участок (
):
;
; (2.149)
. (2.150)
Четвертый
участок (
):
;
; (2.151)
. (2.152)
Пятый
участок (
):
;
; (2.153)
. (2.154)
Составляем
уравнения для определения постоянных
интегрирования
.
При
При
При
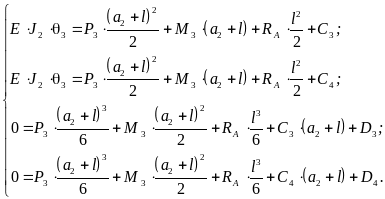
При
Решив
эти уравнения, можно найти постоянные
интегрирования
,
входящие в формулы (2.145) - (2.154),
которые позволяют определить угловые
(шп
= y')
и линейные (yшп)
перемещения оси шпинделя без учета
упругости опор.
3. Расчет дополнительных перемещений оси шпинделя, вызванных податливостью опор
Обозначим упругое перемещение опоры A, а через - упругое перемещение опоры B (рис.2.25).
y
L
x
Рис.2.25. Схема для расчета упругих перемещений опор шпинделя
Значение полного упругого перемещения в опоре определяется, как и для схемы 1, по формуле (2.122). Для определения дополнительного перемещения оси шпинделя yоп и дополнительного угла наклона оп с учетом податливости опор используем следующие выражения:
; (2.155)
. (2.156)
4. Расчет перемещений оси шпинделя, вызванных наличием реактивного момента в передней опоре
Расчетная схема представлена на рис.2.26.
y
RB
RA
Mr
A
V
IV
III
II
I
x
B
Рис.2.26. Расчетная схема для определения угловых и линейных перемещений оси шпинделя, вызванных наличием реактивного момента
Реактивный момент и опорные реакции определяются по формулам (2.128), (2.130), (2.131).
4.1. Определение перемещений оси шпинделя без учета упругости опор от действия реактивного момента в передней опоре
Составляем дифференциальные уравнения изогнутой оси для каждого участка и интегрируем их.
Первый участок ( ):
;
; (2.157)
. (2.158)
Второй участок ( ):
;
; (2.159)
. (2.160)
Третий участок ( ):
;
; (2.161)
. (2.162)
Четвертый участок ( ):
;
; (2.163)
. (2.164)
Пятый участок ( ):
;
; (2.165)
. (2.166)
Составляем
уравнения для определения постоянных
интегрирования
.
При
При
При
При
Решив
эти уравнения, можно найти постоянные
интегрирования
,
входящие в формулы (2.157) - (2.166),
которые позволяют определить угловые
и линейные перемещения оси шпинделя
(соответственно шп.р = y'
и yшп.р),
вызванные реактивным моментом в передней
опоре без учета податливости опор.
4.2. Расчет дополнительных перемещений оси шпинделя, вызванных податливостью опор от действия реактивного момента в передней опоре
Упругие
перемещения опор шпинделя вычисляются
по формуле (2.122), а дополнительное
перемещение оси шпинделя
и дополнительный угол наклона
- по формулам (2.155) и (2.156).
4.3. Суммарные и результирующие значения перемещений оси шпинделя вычисляются по формулам (2.140) - (2.142).
К
y
онструктивная
схема 4.
P3
P5
M5
M3
RA
RB
RC
x
С
B
A
III
VII
VI
V
IV
II
I
Рис.2.27. Расчетная схема для определения угловых и линейных перемещений оси шпинделя
Уравнения статики:
1)
;
; (2.167)
2)
;
. (2.168)
Расчетная схема шпинделя (рис.2.27) является статически неопределимой - чисто опорных реакций, равное трем, превышает число уравнений статики, равное двум. Поэтому для расчета необходимо составить дополнительные уравнения, выражающие условие совместности деформаций, которые вместе с обычными уравнениями равновесия и позволяют определить все опорные реакции и перемещения оси шпинделя.
1. Определение линейного и углового перемещений оси шпинделя
Составляем дифференциальные уравнения изогнутой оси для каждого участка в соответствии с рис.2.27 и интегрируем их.
Первый
участок (
):
;
; (2.169)
. (2.170)
Второй
участок (
):
;
; (2.171)
. (2.172)
Третий
участок (
):
;
; (2.173)
. (2.174)
Четвертый
участок (
):
;
; (2.175)
. (2.176)
Пятый
участок (
):
;
; (2.177)
(2.178)
Шестой
участок (
):
;
(2.179)
(2.180)
Седьмой
участок (
):
;
(2.181)
(2.182)
Составляем
уравнения совместности деформаций,
которые вместе с уравнениями (2.167),
(2.168) позволяют определить постоянные
интегрирования
и
реакции опор
.
При
;
П р и м е ч а н и е.
Здесь и далее
-
податливость соответствующей опоры,
вычисляется по формуле (2.123),
- коэффициент, учитывающий характер
посадки подшипника в опоре (2.122).
При
При
При
При
При
При
Таким
образом, по формулам (2.169) - (2.182) определяются
линейные и угловые перемещения оси
шпинделя без учета защемляющего момента
(
и
).
2. Расчет перемещений оси шпинделя, вызванных наличием защемляющего момента в передней опоре
y
RC
С
VI
Mr
B
A
RA
III
V
IV
II
I
RB
x
Рис.2.28. Расчетная схема для определения угловых и линейных перемещений оси шпинделя
Уравнения статики:
1)
;
; (2.183)
2)
;
. (2.184)
Составляем дифференциальные уравнения изогнутой оси для каждого участка в соответствии с рис.2.28 и интегрируем их.
Первый участок ( ):
;
; (2.185)
. (2.186)
Второй участок ( ):
;
; (2.187)
. (2.188)
Третий участок ( ):
;
; (2.189)
. (2.190)
Четвертый
участок (
):
;
; (2.191)
. (2.192)
Пятый участок ( ):
;
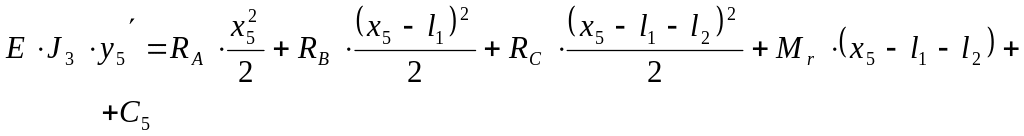; (2.193)
. (2.194)
Шестой
участок (
):
;
; (2.195)
.
(2.196)
Для определения постоянных интегрирования составляем уравнения совместности деформаций.
При
;
При
При
При
При
При
Решение
этих уравнений совместно с (2.183) и (2.184)
позволяет найти реакции опор
и постоянные интегрирования
,
а по формулам (2.185) - (2.196) можно определить
линейные и угловые перемещения оси
шпинделя, вызванные наличием защемляющего
момента в передней опоре:
шп.р
= y'
и yшп.р.
3. Определение суммарных и результирующих значений перемещений оси шпинделя
Суммарные значения угла наклона и перемещений оси шпинделя в одной плоскости определяются по формулам:
(2.197)
Результирующие значения перемещений оси шпинделя вычисляются по формулам (2.141) - (2.142).
2.6.5. Вычисление допустимых перемещений шпинделя.
Допустимый прогиб можно определить исходя из точности обработки на станке. В этом случае значение составляет некоторую долю от допуска наиболее характерной чистовой обработки, а критерием жесткости является условие [29, 33]:
, (2.198)
где
- наибольший прогиб оси шпинделя в месте
резания, непосредственно влияющий на
точность обработки.
Оценка жесткости этим методом применяется для специальных станков, предназначенных для обработки определенного изделия. Для универсальных станков применение данного метода затруднительно в связи с широким диапазоном номенклатуры обрабатываемых деталей.
При приближенных расчетах допустимый прогиб шпинделя выбирают исходя из опыта эксплуатации станков. Часто допустимый прогиб переднего конца шпинделя вычисляется по формуле [31]
, (2.199)
где
- межопорное расстояние.
Недостатком
этого метода может служить тот факт,
что при некотором значении
шпиндель удовлетворяет условию жесткости
,
а при l
= lопт
(оптимальном межопорном расстоянии),
когда lопт
< l,
условие жесткости может и не выполняться,
хотя прогиб переднего конца шпинделя
будет меньше.
Для станков общего назначения допустимый прогиб переднего конца шпинделя предпочтительнее выбирать в зависимости от класса точности станка. Его можно принимать по формуле [31]
, (2.200)
где
- допуск на осевое биение конца шпинделя
по нормам точности станка,
приводится в табл.2.17 - 2.25;
Для удовлетворительной работы зубчатых колес наибольший допустимый прогиб оси шпинделя под ними
, (2.201)
где
- модуль зубчатого колеса, под которым
проверяется прогиб.
Допустимый
угол наклона оси шпинделя в передней
опоре
рад.
Если
условия
или
для данного сечения не выполняются, то
необходимо пересмотреть конструктивные
параметры шпиндельного узла с целью
повышения его жесткости.
Таблица 2.17
Осевое биение шпинделя передней бабки, мкм. ГОСТ 18097-93. Станки токарно-винторезные и токарные.
-
Наибольший диаметр
Осевое биение для станков класса точности
заготовки, мм
Н
П
В
А
10
5
3
2
15
5
3
2
Таблица 2.18