Застосування подвійних та потрійних інтегралів до задач
механіки і фізики
Обчислення маси
плоскої пластинки: Якщо пластинка
лежить у площині
і має форму замкненої області
,
в кожній точці якої задана поверхнева
густина
,
то маса
пластинки обчислюється за формулою:
.
Якщо матеріальне
тіло
має
об’ємну густину
,
то маса тіла обчислюється за формулою:
.
Обчислення статичних моментів: статичні моменти плоскої матеріальної пластинки визначаються за формулами:
.
Якщо тіло знаходиться у просторі , то статичні моменти тіла відносно координатних площин знаходяться за формулами:
.
Координати центра маси: координати центра маси матеріальної пластини обчислюються за формулами:
.
У випадку трьохвимірного простору:
ІДЗ №1
1. Представити
подвійний інтеграл
у вигляді повторного інтеграла із
зовнішнім інтегруванням по
і зовнішнім інтегруванням по
,
якщо область D
задана вказаними лініями:
Область D
зображена на рисунку 1.1, обмежена лініями
,
.
Рис.
1.1
Виразимо змінну через :
Знайдемо точки
перетину ліній
і
:
-
не задовольняє умову.
Отже, маємо:
.
2. Обчислити
подвійний інтеграл по області D,
обмежений вказаними лініями:
Область D зображена на рисунку 1.2.
Рис.
1.2
Оскільки область D симетрична відносно вісі , то:
.
3. Обчислити подвійний інтеграл, використовуючи полярні координати:
.
Область D зображена на рисунку 1.3.
Рис.
1.3
Перейдемо до полярної системи координат:
,
,
.
Маємо:
.
4. Обчислити площу плоскої області D, обмеженої заданими лініями:
.
Подана плоска
фігура обмежена зверху параболою
,
а знизу прямою
(рис. 1.4).
Рис.
1.4
Знайдемо точки перетину параболи із лінією:
Якщо
,
то
.
Якщо
,
то
.
Маємо точки перетину заданих ліній: (2;-6), (-2;-6).
Оскільки область D симетрична відносно осі Оу, то маємо:
.
5. За допомогою подвійних інтегралів обчислити в полярних координатах площу плоскої фігури, обмеженої вказаними лініями:
.
Перейдемо до полярної системи координат:
Рис.
1.5
Рівняння лінії у
полярних координатах має вигляд:
.
Оскільки лінія симетрична відносно осі
Ox й Оу, то площа плоскої
фігури дорівнює:
.
6. Обчислити об’єм тіла, обмеженого заданими поверхнями:
.
Рис.
1.6
Дане тіло обмежено
зверху площиною
(рис. 1.6), тому його об’єм визначаємо
наступним чином:
.
ІДЗ №2
1.
Розставити межі інтегрування у потрійному
інтегралі
,
якщо область V
обмежена вказаними поверхнями. Накреслити
область інтегруваня:
.
Область інтегрування зображена на рисунках 2.1, 2.1а.
Рис. 2.1рис. 2.1а
.
2. Обчислити потрійний інтеграл:
.
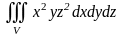
Область
зображена на рис. 2.2.
Рис. 2.2
.
3.
Обчислити потрійний інтеграл за допомогою
циліндричних або сферичних координат:
.
На рисунку 2.3
зображена область V та її
проекція D на
площину
.
Рис.
2.3
Виконаємо деякі
перетворення рівнянь
:
Перейдемо до
циліндричних координат
:
;
;
.
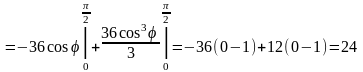4. За
допомогою потрійного інтеграла обчислити
об’єм тіла, обмеженого вказаними
лініями:
.
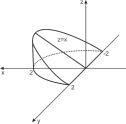Рис.
2.4
Рівняння
визначає зрізаний циліндр, інші поверхні
є площинами (рис. 2.4). Отже, маємо:
.
ІДЗ № 3
1. Обчислити масу неоднорідної пластинки D, обмеженої заданими лініями, якщо поверхнева густина в кожній точці :
.
Для обчислення
маси
плоскої пластини ,поданою поверхневою
густиною
скористаємось фізичним змістом подвійного
інтеграла і формулою
,
де область інтегрування зображена на
рисунку 3.1.
Отже, маса пластинки:
.
Рис.
3.1
2. Обчислити статичний момент однорідної пластини D, обмеженої вказаними лініями, відносно вказаної осі, використавши полярні координати:
.
Рис.
3.2
Перейдемо до полярних координат:
Статичний момент
відносно осі
даної пластини визначається за формулою
.
У полярній системі координат область
D (рис. 3.2) перетворюється
на область
.
Отже, маємо:
.
3. Обчислити координати центра мас однорідного тіла, що займає область V, обмежену заданими поверхнями:
.
Дане тіло (рис. 3.3
)симетричне відносно осі
,
тому
,
.
Рис.
3.3
Перейдемо до циліндричних координат за формулами:
Тоді одержуємо:
Отже,
,
а центр маси має
координати
