Зміст

1. Означення подвійного інтеграла

2. Основні властивості подвійних інтегралів

3. Обчислення подвійного інтеграла

4. Перехід до полярних координат

5. Обчислення площ плоских фігур

6. Обчислення об’єму циліндричного тіла

7. Означення потрійного інтеграла

8. Обчислення потрійного інтеграла

9. Перехід до циліндричних координат потрійному інтегралі

10. Перехід до сферичних координат у просторі

11. Застосування подвійних та потрійних інтегралів до задач механіки і фізики

ІДЗ №1

ІДЗ №2

ІДЗ №3

Список літератури

1. Означення подвійного інтеграла

кратнНехай функція визначена в обмеженій замкнутій області площини . Розіб’ємо область довільним чином на елементарних областей, площі котрих, як і самі області, позначатимемо . У кожній елементарній області виберемо довільну точку .

Інтегральною сумою для функції по області називається сума вигляду: 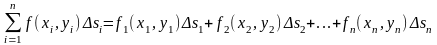. (1)

Діаметром замкнутої обмеженої області називається найбільша відстань між двома точками межі цієї області.

Подвійним інтегралом від функції по області називається границя інтегральної суми (1) за умови, що найбільший із діаметрів , прямує до нуля: .

Подвійний інтеграл позначають так:

.

2. Основні властивості подвійних інтегралів

1. .

2. , де с – const.

3. Якщо область складається із двох областей і , які не мають спільних точок, то

.

4. Якщо дві функції в області задовольняють нерівність , то

.

5. Якщо функція 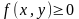в області , то .

.

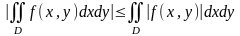3. Обчислення подвійного інтеграла

Область називається правильною в напрямі осі (осі ), якщо будь-яка пряма, яка проходить через внутрішню точку області , паралельно осі (осі ), перетинає межу області у двох точках і .

Якщо область правильна в напрямі осі і проектується на вісь у відрізок , то її межа розбивається на 2 лінії: , яка задається рівнянням , і , рівняння якої 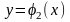. Тоді область задається системою нерівностей: .

При такому заданні області подвійний інтеграл по цій області обчислюється за формулою:

(1.2).

Інтеграл називається повторним або двократним. Інтеграл називається внутрішнім інтегралом. У ньому інтегрування ведеться по змінній , а - const. Отже

.

Якщо область є правильною в напрямі осі , то її можна задати нерівностями: .

Тоді подвійний інтеграл по області обчислюється за формулою:

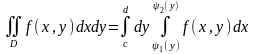(1.3).

Інтеграл називається повторним або двократним.

Інтеграл називається внутрішнім інтегралом. В ньому інтегрування ведеться по змінній , а const. Отже, маємо:

.

Якщо область правильна у напрямі осі та осі , то справедливі формули (1.2) і (1.3).

Якщо порівняти формули (1.2) і (1.3), то маємо:

(1.4).

Перехід від лівої частини формули (1.4), до правої і навпаки називається зміною порядку інтегрування.

4. Перехід до полярних координат

Прямокутні декартові координати , і полярні координати , зв’язані відношенням: .

Якобіан .

Тоді формула переходу до полярних координат набуває вигляду:

.

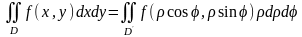де область задана в декартовій системі координат , а - відповідна їй область в полярній системі координат.

5. Обчислення площ плоских фігур

Площа плоскої фігури обчислюється за формулою:

.

У випадку полярної системи координат

.

6. Обчислення об’єму циліндричного тіла

Об’єм циліндричного тіла, обмеженого зверху неперервною поверхнею , знизу площиною і з боків циліндричною поверхнею, твірні якої паралельні осі , а напрямною є контур, що обмежує область , обчислюється за формулою

.

Якщо обчислення ведеться у полярних координатах, то

.

Це є геометричним змістом подвійного інтеграла.