
- •Федеральное агентство по образованию рф
- •Основы рефлектометрии
- •1.1 Рэлеевское рассеяние в волоконных световодах
- •1.2 Бриллюэновское рассеяние в волоконных световодах
- •1.3 Рамановское рассеяние в волоконных световодах
- •1.4 Эффект антистоксова излучения
- •2.1 Рефлектометрия во временной области
- •2.1.1 Рефлектометрия во временной области – традиционный подход.
- •2.1.2 Когерентная временная рефлектометрия.
- •2.1.3 Корреляционная рефлектометрия с применением псевдослучайного сигнала.
- •2.1.4 Слабокорреляционная рефлектометрия.
- •2.1.5 Рефлектометрия на основе счета фотонов.
- •2.2 Рефлектометрия в частотной области
- •2.2.1 Рефлектометрия с частотным сканированием.
- •2.2.2 Рефлектометрия с синтезом функции когерентности.
- •2.3 Поляризационная рефлектометрия
- •2.4 Выводы по главе
- •3.1 Временной когерентный симметричный рефлектометр
- •3.2 Симметричный некогерентный рефлектометр
- •3.3 Симметричный рефлектометр с синтезом функции когерентности
- •3.4 Обсуждение результатов
- •4.1 Изгибные потери в оптических волокнах
- •4.2 Искажения формы контура волоконной решетки Брэгга
- •4.3 Симметричные методы контроля изгибных потерь в вс и искажений контура врб
- •4.3.1 Симметричное зондирование участков вс с изгибными потерями
- •4.3.2 Симметричное зондирование контура врб
- •4.3.3 Мониторинг профиля контуров нескольких врб в волп
- •5.1 Системы несимметричной бриллюэновской рефлектометрии
- •5.2 Симметричный бриллюэновский рефлектометр
- •5.2.1 Физические принципы работы системы с симметричным двухчастотным гетеродинированием.
- •5.2.2 Схема экспериментальной установки.
- •5.2.3 Выводы по разделу.
- •5.3 Вопросы применения бриллюэновского рефлектометра
- •5.3.1 Бриллюэновский датчик механического напряжения вс.
- •3.3.2 Бриллюэновский датчик температуры.
- •6.1 Лазерные диоды
- •6.1.1 Многомодовые (mlm) лазеры, или лазеры с резонаторами Фабри-Перо.
- •6.1.2 Одномодовые (slm) лазеры.
- •6.1.3 Полупроводниковый лазер с распределенной обратной связью (dfb).
- •6.1.5 Лазер с вертикальной резонаторной полостью и излучающей поверхностью (vcsel).
- •7.1 Амплитудно-фазовый метод преобразования одночастотного колебания в симметричное двухчастотное
- •7.2 Спектр выходного излучения амплитудно-фазовых электрооптических уфдли
- •7.3 Влияния параметров преобразования частоты на спектральный состав излучения на выходе аэм
- •7.4 Реализация симметричного уфдли
- •8.2 Конструкция детектора на основе кремниевого фотодиода
- •8.3 Обзор фотодиодных детекторов на основе InGaAs
- •8.4 Лавинные фотодиоды (apd)
- •8.4.1 Рабочие параметры apd.
- •8.4.2 Типы apd.
- •8.4.3 Apd с разделением процессов поглощения и умножения (sam apd).
- •8.5 Оптические приемники
- •Заключение
- •Список литературы
- •Глава 1 6
- •Глава 2 21
- •Глава 3 36
- •Глава 4 45
- •Глава 5 61
- •Глава 6 70
- •Глава 7 79
- •Глава 8 98
4.3 Симметричные методы контроля изгибных потерь в вс и искажений контура врб
4.3.1 Симметричное зондирование участков вс с изгибными потерями
Двухчастотное зондирование участков ВС с изгибными потерями реализовано на основе двухчастотной некогерентной рефлектометрии [24].
Рассмотрим отрезок волокна, который носит изгибной характер и приведен на рис.4.5.
На отрезке
![]() присутствуют внутренние потери α1,
обусловленные релеевским обратным
рассеянием. На отрезке
присутствуют внутренние потери α1,
обусловленные релеевским обратным
рассеянием. На отрезке
![]() присутствуют внешние потери, которые
вызваны микроизгибами оптического
волокна. Так как при приложении
механического натяжения мы получаем
снижение уровня сигнала обратного
рассеяния по сравнению с состоянием
покоя, то потери в зоне дефекта равны
присутствуют внешние потери, которые
вызваны микроизгибами оптического
волокна. Так как при приложении
механического натяжения мы получаем
снижение уровня сигнала обратного
рассеяния по сравнению с состоянием
покоя, то потери в зоне дефекта равны
![]() .
На отрезке
.
На отрезке
![]() ,
где L
– общая длина волокна, мы возвращаемся
к внутренним потерям
,
где L
– общая длина волокна, мы возвращаемся
к внутренним потерям
![]() .
.

Рис.4.5. Структура исследуемого отрезка оптического волокна
В параграфе 3.3 было получено выражение для обратно-рассеянной мощности с рассматриваемого участка:
 ,
(4.9)
,
(4.9)
где
![]()
потери в зоне скрутки, распределенные
по длине волокна.
потери в зоне скрутки, распределенные
по длине волокна.
Взяв отношение постоянных компонент к переменным в выражении (4.9) получим глубину модуляции M, определяемую как
![]() .
(4.10)
.
(4.10)
Два предельных случая могут быть определены как
![]() .
(4.11)
.
(4.11)
Для малых значений
![]() глубина модуляции стремиться к 1 и
глубина модуляции стремиться к 1 и
![]() периодически уменьшается до 0. Для
значений
больше 1 коэффициент модуляции
экспоненциально уменьшается. На рис.4.6
показано экспоненциальное уменьшение
глубины модуляции с увеличением
.
периодически уменьшается до 0. Для
значений
больше 1 коэффициент модуляции
экспоненциально уменьшается. На рис.4.6
показано экспоненциальное уменьшение
глубины модуляции с увеличением
.
M (αLL)
(αLL)
αLL
Рис.4.6. Зависимость глубины модуляции от параметра LL
Если
определить 1% глубину модуляции как
предельно регистрируемую, то система
может быть работоспособна в диапазоне
![]() ,
достигающем 2,7.
,
достигающем 2,7.
При общей длине ВС с изгибными участками в 500 м получим =5,4103 нп/м. Это соответствует потерям ВС с набором изгибных участков в состоянии покоя 27 дБ/км. Собственные потери ВС без изгибных участков составляют 0,5 – 1 дБ/км. При уровне потерь отдельного изгибного участка в состоянии покоя 0,01 дБ/м в ВС может быть около 30 изгибных участков. При большем количестве ВС становится неработоспособным.
Если определить 10% глубину модуляции как предельно регистрируемую, то система может быть работоспособна в диапазоне , достигающем 1,5. При общей длине ВС с изгибными участками в 500 м получим =3103 нп/м. Это соответствует потерям ВС с набором изгибных участков в состоянии покоя 14 дБ/км. При уровне потерь отдельного изгибного участка в состоянии покоя 0,01 дБ/м может быть около 10-15 изгибных участков, что вполне достаточно для обеспечения необходимого отношения сигнал/шум при передаче информации.
4.3.2 Симметричное зондирование контура врб
При анализе взаимодействия симметричного двухчастотного излучения выберем некоторый абстрактный контур, отражающий нормированную зависимость коэффициента отражения от частоты, характерную для ВРБ [25, 26].
Обобщенную амплитудно-частотную характеристику абстрактного контура, на вход которого подается двухчастотный сигнал, можно определить с помощью следующего выражения:
![]() ,
(4.12)
,
(4.12)
где
![]()
обобщенная расстройка контура.
обобщенная расстройка контура.
В принципе возможны два вида анализа: анализ по каждой составляющей отдельно, назовем его дифференциальным, и анализ по огибающей двухчастотного сигнала, назовем его интегральным. Физически оба метода реальны и соответствуют дифференциальному и интегральному зондированию контуров центральных пиков ВРБ. Рассмотрим особенности взаимодействия двухчастотного колебания с контуром при интегральном анализе.
Амплитудно-частотная и фазочастотная характеристики абстрактного контура, на вход которого подается двухчастотный сигнал, представлены на рис.4.7.
По расположению
средней обобщенной расстройки
двухчастот-ного сигнала,
![]() ,
АЧХ и ФЧХ абстрактного контура можно
разделить на три области:
,
АЧХ и ФЧХ абстрактного контура можно
разделить на три области:
Средняя обобщенная расстройка располагается в интервале
 (область I).
В этом случае:
(область I).
В этом случае:
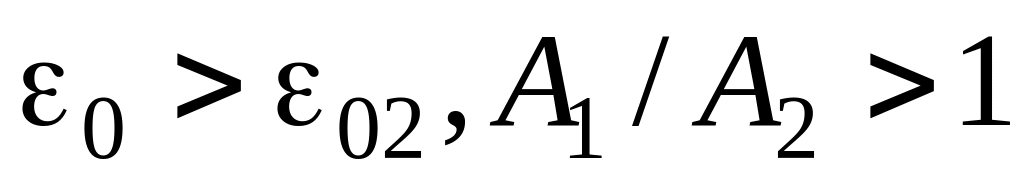 ;
;С
Рис.4.7. АЧХ и ФЧХ абстрактного контура ВРБ
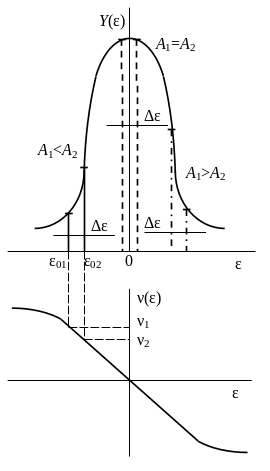 редняя
обобщенная расстройка:
редняя
обобщенная расстройка:
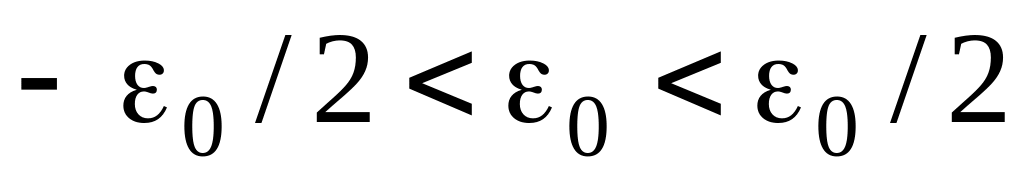 (область II);
(область II);Средняя обобщенная расстройка:
 (область
III).
В этом случае
(область
III).
В этом случае
 .
.
Из рис.4.7 видно,
что значения фаз составляющих выходного
двухчастотного сигнала
![]() ,
,
![]() соответствуют значениям ФЧХ абстрактного
контура на соответству-ющих значениях
обобщенной расстройки составляющих
двухчастот-ного сигнала,
соответствуют значениям ФЧХ абстрактного
контура на соответству-ющих значениях
обобщенной расстройки составляющих
двухчастот-ного сигнала,
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() .
.
С учетом того, что
![]() ,
а
,
а
![]() ,
получим уравнения для зависимостей
фаз составляющих выходного двухчастотного
сигнала от обобщенной расстройки,
,
получим уравнения для зависимостей
фаз составляющих выходного двухчастотного
сигнала от обобщенной расстройки,
![]() и
и
![]() :
:
![]() (4.13)
(4.13)
![]() .
(4.14)
.
(4.14)
Амплитуда и фаза
выходного двухчастотного сигнала, как
следует из рис. 4.7, зависят от значения
средней обобщенной расстройки
и
расстройки между частотами
![]() .
Рассмотрим вопрос об изменении амплитуды
и фазы огибающей выходного двухчастотного
сигнала
.
Рассмотрим вопрос об изменении амплитуды
и фазы огибающей выходного двухчастотного
сигнала
![]() при прохождении его через абстрактный
контур. Огибающая выходного двухчастотного
сигнала описывается выражением вида:
при прохождении его через абстрактный
контур. Огибающая выходного двухчастотного
сигнала описывается выражением вида:
![]() ,
(4.15)
,
(4.15)
где
![]()
результирующее значение амплитуды
выходного двухчастотного сигнала,
результирующее значение амплитуды
выходного двухчастотного сигнала,
![]()
мгновенная фаза,
мгновенная фаза,
![]()
мгновенная частота двухчастотного
колебания.
мгновенная частота двухчастотного
колебания.
Определим
результирующее значение амплитуды
огибающей выходного двухчастотного
сигнала
![]() и получим зависимость коэффициента
амплитудной модуляции. Получим
и получим зависимость коэффициента
амплитудной модуляции. Получим
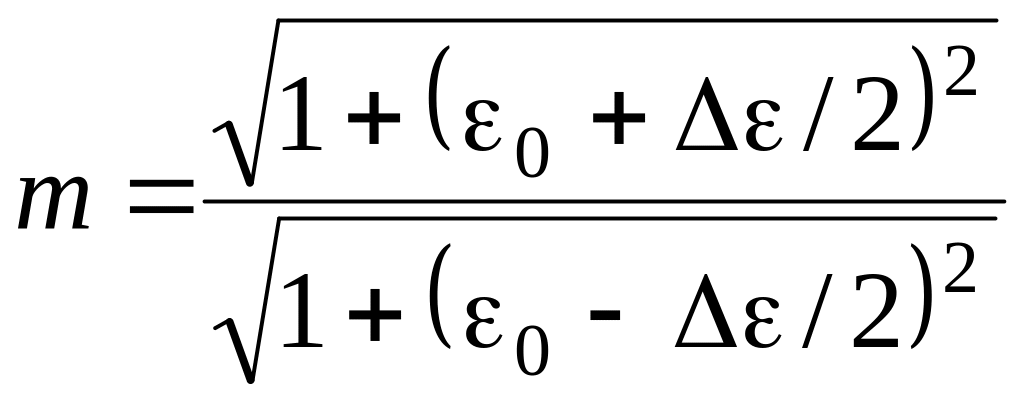 .
(4.16)
.
(4.16)
Из выражения (4.16)
видно, что коэффициент модуляции зависит
от средней обобщенной расстройки
двухчастотного сигнала
и от расстройки между частотами
двухчастотного сигнала
.
Зависимость
коэффициента модуляции от средней
обобщенной расстройки двухчастотного
сигнала,
![]() при разных значениях расстройки между
частотами составляющих
,
представлена на рис.4.8.
при разных значениях расстройки между
частотами составляющих
,
представлена на рис.4.8.
Из рис.4.8 видно,
что кривая зависимости
непрерывная функция с явно выраженным
максимумом в момент
![]() .
Максимум
точка возврата 1-го рода. Функция убывает
до минимума, возрастает до единицы,
снова убывает до минимума. Крутизна
кривой
зависит от расстройки между частотами
.
Оценим эту зависимость.
.
Максимум
точка возврата 1-го рода. Функция убывает
до минимума, возрастает до единицы,
снова убывает до минимума. Крутизна
кривой
зависит от расстройки между частотами
.
Оценим эту зависимость.
Зависимость
крутизны кривой
от расстройки между частотами,
![]() ,
представлена на рис.4.9. Как видно из
рис.4.9 данная кривая имеет явно выраженный
максимум при значении
=2.
То есть, максимальная крутизна кривой
зависимости
соответствует случаю, когда расстройка
между частотами
равна полосе пропускания исследуемого
абстрактного контура. Следовательно,
при значении
=2,
погрешности определения амплитуды
огибающей выходного сигнала будут
минимальны.
,
представлена на рис.4.9. Как видно из
рис.4.9 данная кривая имеет явно выраженный
максимум при значении
=2.
То есть, максимальная крутизна кривой
зависимости
соответствует случаю, когда расстройка
между частотами
равна полосе пропускания исследуемого
абстрактного контура. Следовательно,
при значении
=2,
погрешности определения амплитуды
огибающей выходного сигнала будут
минимальны.
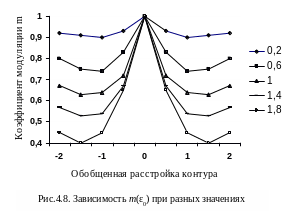
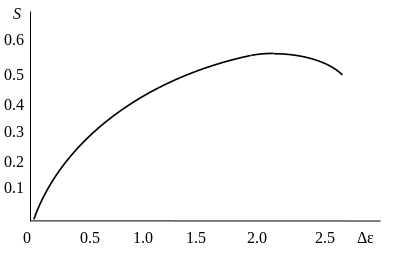
Рис.4.9. Зависимость
![]()
Рассмотрим зависимость разности фаз составляющих выходного сигнала от значения средней обобщенной расстройки сигнала при разных значениях расстройки между частотами . Результаты расчетов представлены на рис. 4.10.
Из рис.4.10 видно,
что графики зависимости
![]()
кривые 3-го порядка проходят через нуль
при
кривые 3-го порядка проходят через нуль
при
![]() .
Функция
непрерывна,
возрастает до максимума, убывает до
минимума и снова возрастает.
.
Функция
непрерывна,
возрастает до максимума, убывает до
минимума и снова возрастает.
Далее определим,
чему равно смещение фазы
![]() огибающей выходного двухчастотного
сигнала относительно фазы входного
сигнала.
огибающей выходного двухчастотного
сигнала относительно фазы входного
сигнала.

Сдвиг фазы огибающей выходного сигнала относительно фазы входного будет равняться:
![]() (4.17)
(4.17)
![]() (4.18)
(4.18)
где
![]()
сдвиг фазы первой и второй составляющих
выходного двухчастотного сигнала, а
сдвиг фазы первой и второй составляющих
выходного двухчастотного сигнала, а
![]()
сдвиг фазы результирующего значения
амплитуды выходного двухчастотного
сигнала
.
Проведя ряд достаточно громоздких
преобразований, которые нет необходимости
отражать в теле работы, обозначив как
сдвиг фазы результирующего значения
амплитуды выходного двухчастотного
сигнала
.
Проведя ряд достаточно громоздких
преобразований, которые нет необходимости
отражать в теле работы, обозначив как
![]() и
и
![]() соответственно выражения
соответственно выражения
![]() и
и
![]() , выражения (4.17) и (4.18) примут вид (4.19) и
(4.20):
, выражения (4.17) и (4.18) примут вид (4.19) и
(4.20):
 (4.19)
(4.19)
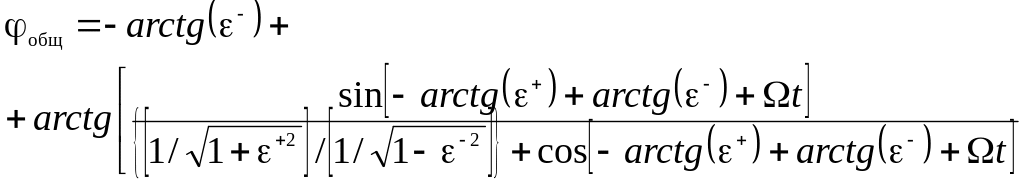 (4.20)
(4.20)
Из выражений
(4.19), (4.20) видно, что смещение фазы
огибающей выходного двухчастотного
сигнала относительно фазы входного
сигнала зависит от значения средней
обобщенной расстройки сигнала
и от значения
расстройки между частотами
.
Результаты расчетов зависимости
![]() при разных
для
при разных
для
![]() ,
по выражению (4.19), представлены на
рис.4.11.
,
по выражению (4.19), представлены на
рис.4.11.
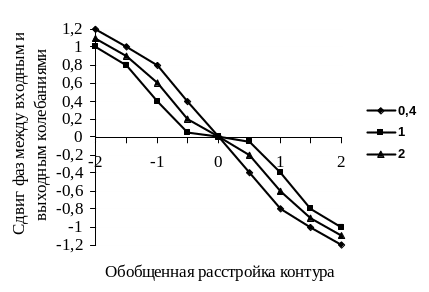
Рис.4.11. Зависимость
![]() при разных
при разных
Из рис.4.11 видно, что при значении средней обобщенной расстройки двухчастотного сигнала , смещение фазы огибающей выходного двухчастотного сигнала относительно фазы огибающей входного сигнала равен нулю. При равенстве расстройки между частотами составляющих двухчастотного сигнала полосе пропускания исследуемого контура, наблюдается максимальная чувствительность к изменению средней частоты двухчастотного сигнала.
Общее выражение
для выходного двухчастотного сигнала
абстрактного контура при
![]() ,
имеет следующий вид:
,
имеет следующий вид:
 (4.21)
(4.21)
Результаты расчетов огибающей выходного сигнала (4.21) приведены на рис.4.12.
Из рис.4.12 видно, что в момент достижения средней частоты двухчастотного сигнала резонансной частоты абстрактного контура, огибающая выходного сигнала по фазе совпадает с огибающей двухчастотного сигнала на входе. При этом коэффициент модуляции огибающей выходного двухчастотного сигнала равен единице.
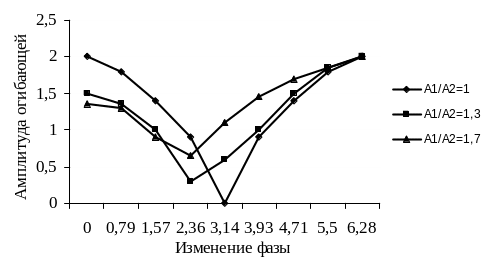
Рис.4.12. Огибающая
выходного двухчастотного сигнала
![]()
Проведя данный анализ можно сделать следующие выводы.
При исследовании воздействия двухчастотного сигнала на абстрактные контуры различных типов при различных способах обработки сигналов на их выходе, показано, что максимальная чувствительность к изменению средней частоты двухчастотного сигнала достигается при значении расстройки между составляющими двухчастотного сигнала равной полосе пропускания исследуемого контура.
Результаты исследований поведения огибающей и мгновенной фазы двухчастотного сигнала на выходе абстрактного контура показали, что в момент достижения средней частоты двухчастотного сигнала резонансной частоты абстрактного контура, огибающая выходного сигнала по фазе совпадает с огибающей двухчастотного сигнала на входе. При этом коэффициент модуляции огибающей выходного двухчастотного сигнала равен единице.
Таким образом, учитывая характеристики крутизны амплитудных и фазовых параметров, можно очень точно определять ширину центрального пика и центральную частоту ВРБ, а, следовательно, регистрировать изменение частоты ее настройки и формы контура.
