3.2 Симметричный некогерентный рефлектометр

Рассмотрим отрезок ВС, который представлен на рис.3.2. На отрезке присутствуют внутренние потери , обусловленные рэлеевским обратным рассеянием. На отрезке присутствуют внешние потери, которые вызваны микроизгибами ВС (дефект). Так как при приложении механического натяжения мы получаем снижение уровня сигнала обратного рассеяния по сравнению с состоянием покоя, то потери в зоне дефекта равны . На отрезке , где L – общая длина ВС, мы возвращаемся к внутренним потерям α₁.

Для отрезка мощность сигнала обратного рассеяния с участка может быть описана как

, (3.7)

где  мощность источника зондирования,  коэффициент внутренних потерь (нп/м), A – фактор обратного рассеяния и k_w – волновой вектор для ЛЧМ-модуляции на АМ-поднесущей.

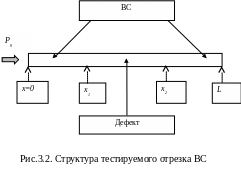
Аналогично для и на рис.3.2 получим

, (3.8)

. (3.9)

Выражения (3.7) – (3.9) могут быть проинтегрированы и объединены в общее уравнение для обратнорассеянного сигнала. Примем , тогда в состоянии покоя обратно-рассеянная мощность с рассматриваемого участка может быть представлена как

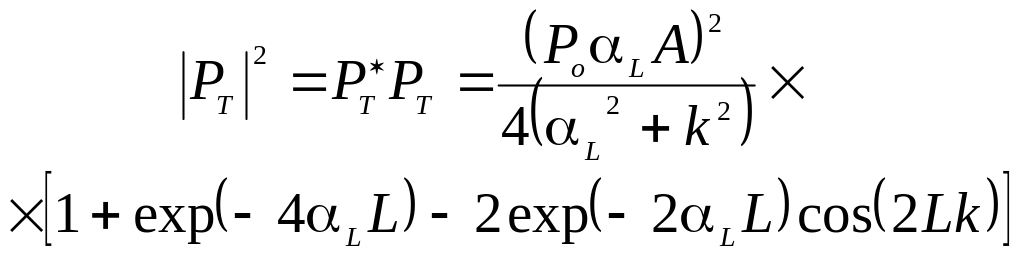. (3.10)

где  потери в зоне изгибов ВС, распределенные по длине ВС.

Если ввести линейное изменение частоты с постоянной скоростью , то мы получим периодическое изменение . Мы можем записать косинусную составляющую в уравнении (3.10) с учетом линейного изменения частоты как

. (3.11)

Возможности анализа рефлектометрического сигнала в некогерентном симметричном рефлектометре могут быть развиты в двух направлениях. Для первого из них, взяв отношение постоянных компонент к переменным в выражении (3.11) получим коэффициент (глубину модуляции), задавшись которым, как некоей предельно регистрируемой величиной, можно определить максимальную длину тестируемого ВС или максимальные общие потери и максимальное количество тестируемых узлов (мультиплексоров, ответвителей и т.д.). Второе направление определяется возможностью тестирования избирательных элементов ВС, например волоконных решеток Брэгга.

3.3 Симметричный рефлектометр с синтезом функции когерентности

При использовании пошагового изменения частоты, а не постоянного свипирования изменение частотнозависимой амплитуды и фазы зондирующего сигнала с преобразованием Фурье позволяет сформировать отклик подобный отклику временного рефлектометра. Данный метод называется методом с синтезом функции когерентности.

Появившиеся работы о применении методов синтеза когерентных функций треугольной и прямоугольной формы, определяют перспективность применения ступенчатой ЛЧМ и в данных системах.

Спектральную плотность ЛЧМ сигнала можно определить, пользуясь общей формулой

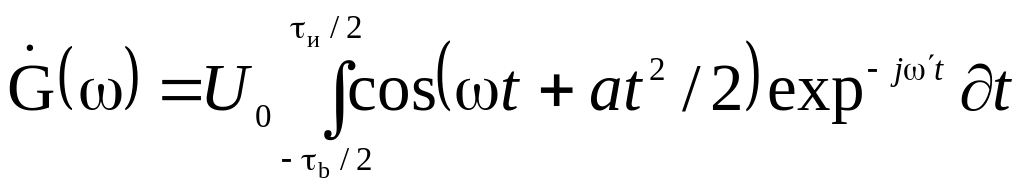. (3.12)

Расчет функции показывает, что при больших значениях m100 форма спектра ЛЧМ сигнала близка к прямоугольной. Поскольку в частотных системах используется непрерывное излучение, то излученный оптический сигнал является гармоническим и модулированным. Отраженный от локальной неоднородности ВС или элемента ВОЛП сигнал представляет собой его запаздывающее повторение, дополнительно модулированное за счет изменения характеристик объектов отражения и собственно ВС, как среды распространения. Поскольку и сигнал гетеродина также является гармоническим и модулированным, то при взаимодействии его с отраженным сигналом всегда будут выполняться условия «почти когерентного» излучения.

Сигнал на выходе фотодетектора системы с синтезированием функции когерентности может быть описан в виде

, (3.13)

где   коэффициент отражения неоднородности, n  изменение коэффициента преломления,  закон изменения частоты .

Интеграл в фигурных скобках представляет синтезируемую функцию когерентности. Основное преимущество метода заключается в возможности получения прямого измерения  без проведения сложных вычислений, что объясняется возможностью приведения синтезированной функции когерентности и функции корреляции по n к виду дельта-функции. Сканирование пика функции когерентности достигается изменением значения частоты , при этом пространственное разрешение будет определяться как

, (3.14)

где N – число ступеней аппроксимации функции когерентности.

Преимущество амплитудно-фазовых симметричных УФДЛИ заключается в возможности перестройки частоты по заданному закону с заданной скоростью. При этом , а следовательно может быть достигнуто очень высокое пространственное разрешение. Основное ограничение на достижение пространственного разрешения в субмиллиметровой области накладывает нелинейность модуляционных характеристик электрооптических модуляторов, которая приводит как к искажению законов модуляции и синтеза функции когерентности, так и к появлению ее субпиков (паразитных спектральных составляющих). Последнее приводит к снижению динамического диапазона измерений, который в основном определяется характеристиками гетеродинного детектирования.

Рассмотрим влияние нелинейности модуляционных характеристик на возможность получения достоверных пространственных измерений. Опираясь на результаты классических исследований [11], можно определить требования к функциям удовлетворяющим возможности проведения ЛЧМ измерений:

• на протяжении каждого полупериода модуляции связь между – частотой, определяющей координату z, и собственно z должна быть однозначной;

• во всем заданном интервале измерений L средняя за полупериод частота должна линейно зависеть от времени запаздывания, определяемого координатой z.

Легко видеть, что при выполнении второго условия первое условие выполняется автоматически. К группе функций, удовлетворяющих второму условию, относятся функции [11]: не имеющие ни экстремумов, ни точек перегиба; не имеющие экстремумов, но имеющие точки перегиба; имеющие два экстремума, разделенные отрезком времени, меньшим, чем минимальное время задержки. При определенных условиях могут рассматриваться синусоидальное и прямоугольное изменение частоты.

Получаемые с помощью амплитудно-фазовых симметричных УФДЛИ спектральные соотношения (количественные характеристики которых будут рассмотрены в главе 6) безусловно удовлетворяют требованиям, налагаемым на возможность использования функций для ступенчатого ЛЧМ зондирования ВС.

С другой стороны эквивалентное импульсному синтезированное зондирование ВС приводит к возможности измерения температурных полей, которое характерно для импульсных систем с бриллюэновским или рамановским рассеянием. При этом сканирование двухчастотного излучения позволяет раздельно локализовать стоксовскую и антистокосовскую компоненты.