Аналитические модели потоков сообщений
В локальных вычислительных сетях и системах в случае пиковых нагрузок возникают очереди сообщений, приводящие к задержке их обработки и передачи.
Известно, что при анализе и проектировании ЛВС необходимо ответить на следующие вопросы:
- какова длина очереди сообщений?
- сколько времени сообщению приходится ждать в очереди?
- какова вероятность передачи сообщения.
Ответы на поставленные вопросы были получены на основе применения результатов теории массового обслуживания. Принцип теории массового обслуживания при расчете ЛВС основан на том, что события, вызывающие ввод данных в систему от абонентских аппаратов, происходят независимо друг от друга. Поскольку таких абонентов много, то вероятность поступления сообщения в данный интервал времени от какого-либо конкретного абонентского аппарата, весьма мала. По этой же причине поступление в это же время одного или даже нескольких сообщений от любых, безразлично каких, источников является весьма вероятным событием.
Распределение Пуассона
Если поток сообщений, поступающих на обработку, удовлетворяет требованиям:
- стационарности, т.е. вероятность свершения некоторого числа событий за данный интервал времени не зависит от расположения этого интервала, а зависит лишь от его длины;
- независимости событий, т.е. сообщения поступают независимо друг от друга;
ординарности - сообщения поступают по одному и поступление одновременно двух сообщений невозможно, то такая система, сообщений подчиняется закону распределения вероятностей Пуассона, а поток сообщений носит название "пуассоновский".
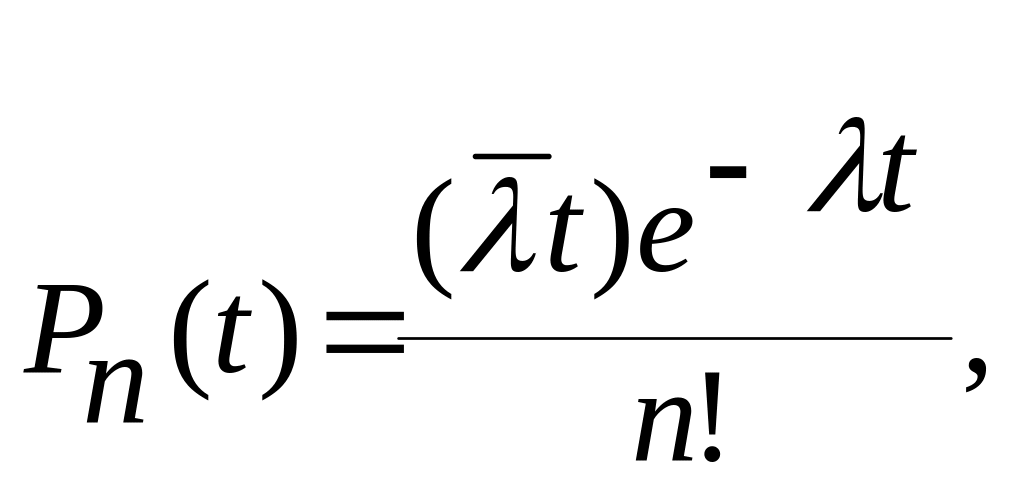(1)
где
- вероятность того, что в течение интервала
времени t поступит на обработку ровно
n сообщений;
-
средняя интенсивность поступления
сообщений в одну секунду.
Очевидно, что
- среднее число сообщений, поступающих
в систему за рассматриваемый интервал
времени t.
(2)
характеризует
закон плотностей распределения
вероятностей того, что при среднем числе
сообщений, поступающих за некоторый
промежуток времени, в систему поступит
ровно
сообщений.
Нетрудно показать, что
(3)
Дисперсия Dn(t), характеризующая отклонение числа заявок от среднего значения, определяется для закона Пуассона:
(4)
среднеквадратическое отклонение
(5)
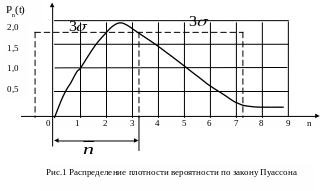
График Pn(t) = f(n) при заданном значении n показан на рис.1. Следует отметить, что в интервале З укладывается 95% площади, ограниченной кривой Рп (t) и осью абсцисс.
Функция распределения вероятностей Fn(t) определяет вероятность того, что за данный интервал времени t в систему поступит не более n сообщений:
(6)
Очевидно, что
(7)
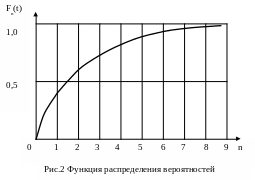
График Fn
(t) для заданного значения
приведен
на рис. 2.
Из соотношения (1), характеризующего закон Пуассона, определим вероятность того, что за время t не поступит ни одного сообщения:
(8)
Вероятность того, что за промежуток времени t поступит хотя бы одно сообщение
(9)
Функция F(t) - есть функция распределения вероятностей того, что действительный интервал между двумя соседними сообщениями окажется меньше или равен /. Время t называют еще периодом поступления сообщений. Плотность распределения вероятностей
(10)
определяется как производная F(t). Произведение Р() указывает вероятность того, что период поступления соседних сообщений находится в интервале от t до t +. Среднее значение интервала между двумя соседними сообщениями определяется по обычной формуле:
(11)
Действительно, среднее время между двумя соседними сообщениями есть величина, обратная средней частоте поступления сообщений Среднеквадратическое отклонение (т) определяется через дисперсию D().
Откуда
(12)
откуда
(13)
Для экспоненциального закона распределения временных характеристик справедливо соотношение:
(14)
Соответствие экспериментальных данных соотношению (14) говорит о том, что распределение плотностей вероятностей экспоненциально.