Қазақстан Республикасы Білім және ғылым министрлігі

Академик Е.А. Бөкетов атындағы

Қарағанды мемлекеттік университеті

Мауленова Т.К

Азобензолдар құрылымы мен қасиеттерін DFT әдісімен есептеулер.

Дипломдық жұмыс

5В060600 – «Химия» мамандығы

Қ арағанды 2015

Қазақстан Республикасы Білім және ғылым министрлігі

Академик Е.А. Бөкетов атындағы

Қарағанды мемлекеттік университеті

«Қорғауға жіберілді»

Физикалық және аналитикалық химия кафедрасының меңгерушісі

_____________А.С. Масалимов

Дипломдық жұмыс Тақырыбы: «Азобензолдар құрылымы мен қасиеттерін dft әдісімен есептеулер.»

5В060600 – «Химия» мамандығы

Орындады: Мауленова Т.К

Ғылыми жетекшісі х.ғ.к., доцент Л.Қ. Абуляисова

Қ арағанды 2015

МАЗМҰНЫ

	Кіріспе………………………………………………………………….	6
1	Азобензол	9
1.1		10
1.2		11
1.3		13
1.4		14
2		16
2.1		18
2.2		22
2.3		27
2.4		32
3		37
3.1		39
3.1.1		43
3.1.2		47
4		49
4.1		49
4.1.1		51
4.1.2		54
4.1.3		55
4.1.4		57
4.1.5		60
4.2		62
4.2.1		64
4.2.2		67
4.2.3		68
4.2.4		69
4.2.5		72
	Қорытынды…………………………………………………………….	75
	Пайдаланылған әдебиеттер тізімі……………………………………	78
	Қосымшалар……………………………………………………………	80

Кіріспе

1.1

15. Теория функционала плотности.

«Традиционные» методы квантовой химии, основанные на методе Хар-три-Фока в качестве отправной точки и использующие представление о вол-новой функции как характеристики состоянию квантовой системы, в прин-ципе могут дать точный ответ о строении, энергии и химических свойствах исследуемого соединения. Для этого необходим полный учет энергии корре-лированного движения электронов и представление АО, не содержащее по-грешности базисного набора. В настоящий момент такие расчеты возможны только для самых простых молекул. Даже наиболее удачные приближения к Full CI, такие как СС или MCSCF, применимы к молекулярным системам, содержащим порядка 10 тяжелых атомов.

Очень привлекательной альтернативой этим методам является подход, основанный на использовании теории функционала плотности (Density Func-tional Theory, DFT). Оказалось, что DFT методы, несмотря на подчас очень грубые приближения, во многих случаях и для многих систем дают результа-ты на уровне или даже превышающие по точности таковые, полученные ме-тодами объединенных кластеров или квадратичного КВ. И это при затратах времени и компьютерных ресурсов таких же, как и в методе Хартри-Фока! Неудивительно, что лучшие DFT методы сейчас сильно потеснили HF мето-ды. Кратко рассмотрим основные понятия и представления теории функцио-нала плотности.

15.1. Общие положения.

Что такое функционал? Функция – это соответствие одного числового ряда другому, т.е. функция «берет» число и «возвращает» сопоставленное ему число: y = f(x). Функционал же ставит в соответствие число и функцию, которая, в свою очередь, сопоставлена другому числу, т.е. y = F[f(x)] или просто y = F[f]. С функционалом можно проводить те же операции, что и с функцией (например, дифференцировать): ∫=−+=dxxfxfFfFffFfF)()(][][][δδδδδ )()()()()()(122121FxfFFxfFFFxfδδδδδδ+= и т.д.

В методах DFT ключевой физической величиной является электронная плотность ρ, которая суть функция координат всех составляющих систему электронов. Для одного электрона в методе Хартри-Фока 2)()(rriiϕρ=, а электронная плотность, создаваемая всеми электронами молекулы равна

2

Σ==Niitotalrr12)()(ϕρ.

В течение многих лет использование электронной плотности для описа-ния квантовой системы было скорее интуитивным, чем строго обоснован-ным. Электронная плотность гораздо более привлекательна, чем волновая функция. Во-первых, она физически определена и, в принципе, измеряема в отличие от волновой функции, не имеющей физического смысла. Во-вторых, волновая функция N-электронной системы зависит от 3N координат электро-нов (или даже 4N, если принимать во внимание спин), тогда как электронная плотность всегда есть функция от трех координат независимо от числа элек-тронов в молекуле. Проблема заключается в том, что было неизвестно, суще-ствует ли взаимозависимость между электронной плотностью и энергией, и если она существует, каков ее конкретный вид.

15.2. Теорема Хоэнберга и Кона.

В 1964 году Хоэнберг и Кон доказали теорему, что свойства основного состояния являются функционалом электронной плотности ρ, что явилось вторым рождением DFT. Конкретнее говоря, согласно теореме Хоэнберга и Кона энергия основного состояния молекулы является функционалом электронной плотности Etotal[ρ], и энергия минимальна, если ρ является точной электронной плотностью основного состояния.

Эта теорема доказывается с использованием принципа «от обратного». Рассмотрим следующую цепочку логических рассуждений.

1. Пусть нам известно точное значение электронной плотности основно-го невырожденного состояния ρ(r).

2. Допустим, что плотности ρ(r) соответствуют два различных операто-ра – потенциалы V и V’.

3. Следовательно, для одной и той же плотности существуют

а) два различных Гамильтониана H и H’;

б) два различных набора собственных волновых функций Ψ и Ψ’;

в) два различных значения E0 и E0’, E0 = <Ψ|H|Ψ> и E0’ = <Ψ’|H’|Ψ’>.

4. Используя вариационный принцип (см. раздел 9.2), рассчитаем энер-гию для Ψ’ с гамильтонианом H:

.)'('')'ˆˆ(''')'ˆˆ('''ˆ''ˆ'000∫∫∫∫∫−+=Ψ−Ψ+==Ψ−Ψ+ΨΨ=ΨΨ<drVVEdrVVEdrHHdrHdrHEρ

5. Аналогичным образом рассчитаем энергию для Ψ с гамильтонианом H’.

∫∫∫∫∫−−=Ψ−Ψ−==Ψ−Ψ+ΨΨ=ΨΨ<.)'()'ˆˆ()ˆ'ˆ(ˆ'ˆ'000drVVEdrVVEdrHHdrHdrHEρ

6. Сложим два последних уравнения:

3

E0 + E0’ < E0 + E0’.

Получили абсурдный результат. Следовательно, исходная посылка о возможности существования двух различных потенциалов для одной элек-тронной плотности ρ(r) неверна! Отметим также, что доказательство опира-лось на вариационный принцип, поэтому оно справедливо только для основ-ных состояний.

15.3. Ранние методы теории функционала плотности.

Хотя теорема Хоэнберга и Кона дает строгое доказательство взаимосвя-зи Etotal и ρ, она не дает никакого правила, чтобы построить этот функционал. Полная энергия квантовой системы равна

Etotal = T + Ene + J + K + Enn.

При использовании приближения Борна-Оппенгеймера энергия межъя-дерного отталкивания постоянна, Enn = const. Энергия притяжения электро-нов к ядрам Ene и кулоновская энергия отталкивания электронов J могут быть выражены через электронную плотность точно так же, как в теории Хартри-Фока: drrrZdrrrZrrENNiMiine)()()()]([ρϕϕρααααΣ∫ΣΣ∫−=−= 21212121222121)()(21)(1)(21)]([drdrrrrrdrdrrrrrrJjiij∫∫∫∫−=−=ρρϕϕρ

В ранних попытках вывести функционалы для кинетической (T) и об-менной (K) энергий систему электронов рассматривали как однородный электронный газ. Так, в модели Томаса-Ферми-Дирака: .343,)(][,)3(103,)(][3/13/43/223/5⎟⎠⎞⎜⎝⎛=−===∫∫πρρπρρXXDFFTFC drrCKC drrCT

Эти уравнения использовали в физике твердого тела, но для химических систем они оказались непригодны: модель Томаса-Ферми-Дирака не пред-сказывала химического связывания, т.е. молекулы в рамках этой теории про-сто не существовали! Для исправления ситуации был использован так назы-ваемый подход градиентной коррекции, согласно которому T и K зависят не только от плотности ρ, но и от ее производных. Подробнее об этом см. ниже.

Нельзя не упомянуть такого предшественника DFT методов, как метод Xα Слэтера (1951). Слэтер дал приближенное решение хартри-фоковских Ћ9_ИҐ-___‰уравнений, причем обменная энергия рассчитывается в виде []∫+⎟⎠⎞⎜⎝⎛−=,)()(4349],[3/43/43/1drrrEXβαβααρρπαρρ

4

где α – подобранный параметр для каждого атома Периодической таблицы. Для большинства атомов α = 0.7 ÷ 0.8. Не следует путать этот параметр с греческими символами в обозначениях α и β. Эти обозначения относятся к так называемым спиновым плотностям, т.е. электронным плотностям, созда-ваемым отдельно системами α и β электронов.

15.4. Метод Кона-Шама.

Начало использованию DFT методов в вычислительной химии положило внедрение в расчетную схему орбиталей, предложенное Коном и Шамом. Основная идея теории Кона-Шама состоит в разделении функционала кине-тической энергии на две части, первая вычисляется точно с использованием формально построенных орбиталей, отвечающих системе невзаимодейст-вующих электронов TS, вторая представляет собой поправочный член – кор-рекцию (correction), TC:

T[] = TS[] + TC[], .21][2Σ∇−=MiiiiSTϕϕρ

Несомненным достоинством предложенного подхода является то, что описание молекулярной системы практически полностью аналогично хартри-фоковскому, а именно:

а) для построения орбиталей используется метод ЛКАО (см. раздел 11.4);

б) описание атомных орбиталей осуществляется теми же базисными на-борами (см. разделы 12.2 – 12.6);

в) орбитали и их энергии находятся итерационным путем с помощью процедуры самосогласования. Аналогами уравнений Хартри-Фока-Рутаана (см. раздел 11.5) в теории функционала плотности являются уравнения Кона-Шама:

Σ===−NiiN cSK1.,...,2,1,0)(ννμνμνμε

Матрица Kμν в DFT приближениях аналогична матрице Фока. Энергии орбиталей Кона-Шама находят из векового уравнения: .0=−μνμνεSKi

Несколько слов о недостатках метода Кона-Шама. Орбитали Кона-Шама и их энергии не имеют такого значения, как хартри-фоковские орбитали и εi, равные в рамках теоремы Купманса потенциалу ионизации с противополож-ным знаком, –IP. Данные орбитали сконструированы лишь так, чтобы давать наилучшее описание электронной плотности ρ, а энергии орбиталей Кона-Шама позволяют вычислить Etotal как функционал электронной плотности.

Тем не менее, практика использования DFT методов показала, что орби-тали Кона-Шама во многих случаях очень близки к хартри-фоковским орби-

5

талям, что оправдывает их использование в качестве пробной волновой функции даже в таких проблемных методах как CASSCF.

Коррекция к кинетической энергии TC в методе Кона-Шама просто включается в обменный член K и, таким образом, полная электронная энер-гия в теории функционала плотности вычисляется в виде:

EDFT[ρ] = TS[ρ] + Ene[ρ] + J[ρ] + EXC[ρ],

TS – кинетическая энергия, рассчитываемая с помощью детерминанта Слэте-ра (S), составленного из орбиталей Кона-Шама; EXC – корреляционно-обменный функционал, причем обменный член дает больший вклад (напри-мер, для атома Ne EX = -12.11 a.e., EC = -0.39 a.e.).

15.5. Сравнение методов Хартри-Фока и Кона-Шама.

Как видно из предыдущего обсуждения и уравнения для полной энергии EDFT, для точного решения многоэлектронной задачи осталось найти корре-ляционно-обменную энергию, включающую в себя, как видно из названия, энергию электронной корреляции. Другими словами, теория функционала плотности, несмотря на однодетерминантное представление волновой функ-ции, учитывает корреляционную энергию и, в принципе, способна это сде-лать точно. Единственная проблема состоит в том, что вид корреляционно-обменного функционала неизвестен, а потому необходимо искать его при-ближенное описание. Прежде чем познакомиться с существующими подхо-дами к описанию EXC дадим краткую сравнительную характеристику теорий Хартри-Фока и функционала плотности.

Как отмечено выше, обе теории имеют очень похожий математический аппарат, основаны на вариационном принципе, используют итерационную процедуру и имеют примерно одинаковую затратность порядка N4. В то же время, между методом Хартри-Фока и DFT существуют и принципиальные различия, которые сформулируем в виде вопросов:

1. Возможно ли в принципе получение точного решения? Если бы было известно точное значение EXC, DFT давала бы возможность вычислить точное значение полной энергии, включающее электронную корреляцию. И это при таких же вычислительных затратах, как и для расчета некоррелиро-ванной хартри-фоковской энергии! Правда не исключено, что точный EXC[ρ] функционал может быть настолько сложным, что вычислительные затраты станут сопоставимыми с таковыми для точного решения уравнения Шредин-гера традиционными методами волновой механики. Метод Хартри-Фока в принципе не способен дать точного решения волнового уравнения, а дости-жим лишь хартри-фоковский предел (см. раздел 12.6 и 13.1).

2. Строго ли решаются уравнения теории? В методе Хартри-Фока система одноэлектронных уравнений решается строго, т.к. итерационная процедура в принципе позволяет достичь любого разумно малого порога сходимости решения. Хотя в DFT приближениях также используется проце-дура самосогласования, элементы матрицы Кона-Шама рассчитываются при-ближенно, нестрого, т.к. неизвестен точный вид корреляционно-обменного функционала.

6

Поскольку точный вид EXC[ρ] пока неизвестен, актуальным является во-прос: какие вычислительные затраты необходимы для получения результата заданной точности? В этом отношении методы DFT выглядят чрезвычайно привлекательными.

15.6. Корреляционно-обменный функционал.

Оказывается возможным доказать, что обменно-корреляционный по-тенциал является уникальным функционалом, строгим для всех систем. Од-нако конкретный вид этого потенциала неясен. Различные DFT методы отли-чаются друг от друга только выбором формы EXC[ρ] функционала, наличием различных наборов подгоночных параметров.

Обычным подходом является разделение EXC на обменный EX и корреля-ционный EC потенциалы, хотя строгость такого разделения не установлена:

()(.)()()()(][][][ ) ∫∫+=+=drrrdrrrEEECXCXXCρερρερρρρ

15.6.1. Приближение локальной плотности.

Предложено несколько вариантов конкретного вида функционалов EX и EC. В ранних и более простых вариантах DFT использовали приближение ло-кальной плотности (или более общий случай – локальной спиновой плотно-сти – Local Spin Density Approximation, LSDA), предполагающее, что локаль-но электронная плотность представляет собой однородный электронный газ, что эквивалентно медленно изменяющейся функции плотности. Обменная энергия вычисляется по формуле Дирака:

(),2][3/13/13/1βαρρρε+−=XLSDAXC

коэффициент CX имеет тот же смысл, что и приведенный в разделе 15.3.

Это же уравнение может быть записано в терминах общей плотности и спиновой поляризации ζ:

[].,)1()1(2][3/43/43/13/1βαβαρρρρζζζρρε+−=−++−= CXLSDAX

Корреляционную энергию однородного электронного газа рассчитывают по аналитической интерполяционной формуле Воско, Уилка и Нюсэ (Vosko, Wilk, Nusair), содержащей неполяризованную (ζ = 0) и поляризованную (ζ = 1) составляющие: [],)()0,()1,()1()0()()()0,(),(44ζζεεζζεεζεfrrffrrrScScSaScSVWNC−++−′′+=

где .)12(22)1()1()(433/13/43/43/1−−−++=⎟⎠⎞⎜⎝⎛=ζζζπρfи rS

7

Функционалы εc и εa определяются по формулам, содержащим ряд под-гоночных параметров. Так согласно формуле, предложенной Пердью и Ван-гом (Perdew, Wang, 1991, PW91): ,)(211ln)1(24433221291/⎟⎟⎠⎞⎜⎜⎝⎛+++++−=xxxxaxaPWacββββαρε

где x = rS1/2; a, α, β1, β2, β3, β4 – некоторые константы.

Точность методов, основанных на приближении LSDA сопоставима с точностью хартри-фоковских методов.

15.6.2. Методы градиентной коррекции.

Более точные результаты дают методы градиентной коррекции (General-ized Gradient Approximation, GGA), связывающие EX и EC не только с плотно-стью ρ, но и с ее первой (∇ρ) и второй (∇2ρ) производными. Было предложе-но несколько функциональных зависимостей в виде поправок к LSDA функ-ционалам. Например, обменная поправка Бекке (Becke, 1988): .,sinh61,3/4123/1888888ρρββρεεεε∇=+−=ΔΔ+=−x xxx BXBXLDAXBX

Параметр β подобран по известным данным для атомов. Также широко используется обменный и корреляционный функционалы с поправками, оп-ределенными Пердью и Вангом. Например, формула для обменного функ-ционала имеет вид: ,)(sinh1))exp(()(sinh125211224321191⎟⎟⎠⎞⎜⎜⎝⎛++−+++=−−xaxaxaxbxaaxaxaLDAXPWXεε

где a1-5 и b – подобранные константы, а x имеет тот же смысл, что и в преды-дущем уравнении. Корреляционный функционал имеет вид:

.9191PWCLDACPWCεεεΔ+=

Аналитическую формулу для поправки к корреляционному функциона-лу PW91 можно найти в специальной литературе. 91PWCεΔ

Также был предложен ряд функционалов с градиентной коррекцией (не поправок!). Например, один из наиболее популярных корреляционных функ-ционалов предложен Ли, Янгом и Парром (Lee, Yang, Parr, LYP): ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∇+∇−∇−−∇+∇+−+−=−222222223/123218)1(4αββαβαααααρρρρρρρρρρωρρρρεXabdaLYPC

()()()()(),112)45(747)2(1442212223/83/83/2ββααβαβαρρρρδρρρδρδρρ∇+∇−+∇+∇××−−∇−++=−FCX

8

,1,)1()exp(3/13/1313/143/13/1−−−−++=+−=ρρρρρωddcρδ dc/

константа CF определена в разделе 15.3, a, b, c и d – параметры, определен-ные подгонкой к экспериментальным данным для атома гелия. Добавление нелокальных членов к LSDA функционалу заметно повышает качество рас-четов как структурных параметров молекул, так и энергетических характери-стик.

15.6.3. Гибридные методы.

Наконец, получили развитие так называемые гибридные методы, в кото-рых в выражение для EX вносится вклад, рассчитываемый так же, как обмен-ная энергия в методе Хартри-Фока (только используются, конечно, орбитали Кона-Шама).

Например, трехпараметровый функционал Бекке (B3) – пример гибрид-ного функционала:

,)1(883GGACVWNCBXHFXLSDAXBXCEcEEbEaEaEΔ⋅++Δ⋅+⋅+−=

где хартри-фоковская обменная энергия HFXE с вкладом a входит в выраже-ние для обменного функционала. Формулы для второго и четвертого членов суммы приведены в разделе 15.6.1, для третьего слагаемого – в разделе 15.6.2. Последний член суммы – есть градиентная коррекция корре-ляционного функционала. В зависимости от вида поправки получается та или иная конкретная реализация DFT гибридного метода. Так, использование по-правки Пердью и Ванга (GGA ≡ PW91) дает популярный метод B3PW91. В наиболее используемом в настоящее время DFT методе вместо ис-пользуется корреляционный функционал Ли, Янга и Парра LYP, приводя к известному акрониму B3LYP. Так как функционал LYP содержит и локаль-ный, и _ё_ИЋ9____нелокальный члены, то корреляционно-обменный функционал метода B3LYP в действительности имеет вид: GGACEΔGGACEΔ

,)1()1(883LYPCVWNCBXHFXLSDAXLYPBXCEcEcEbEaEaE⋅+−+Δ⋅+⋅+−=

a, b и c – константы, которые были подобраны Бекке с использованием на-дежных экспериментальных данных для репрезентативного набора сравни-тельно простых химических соединений (так называемый G1-набор).

Другие примеры гибридных функционалов: MPW1PW91 – однопара-метровый гибридный функционал с модифицированным обменным функ-ционалом Пердью и Ванга и корреляционным функционалом PW91, данный DFT метод используется для расчета химических сдвигов и констант сверх-тонкого взаимодействия спектров ЯМР с превосходной степенью точности; G961LYP – однопараметровый гибридный функционал с обменным функ-ционалом Джилла G96 и корреляционным функционалом LYP и т.д.

Широкое практическое использование гибридных DFT методов обу-словлено уникальным сочетанием низкой затратности приближения и высо-кой степени точности результатов расчетов, сравнимой (а иногда и превосхо-

9

дящей!) с точностью таких сложных многодетерминантных методов как MP2, MP4, QCISD и CCSD.

15.7. Вычислительные особенности DFT методов.

Орбитали Кона-Шама ищут в виде линейной комбинации АО аналогич-но методу Хартри-Фока-Рутаана

.Σ⋅=Niicαααχϕ

Коэффициенты разложения cαi определяют по уравнениям, аналогичным уравнениям Хартри-Фока-Рутаана, при этом матрица Фока заменяется на матрицу Кона-Шама: .212XCneKSVJVH+++∇−=

Элемент матрицы

∫=.drHHKSβααβχχ

Все вычисления аналогичны методу Хартри-Фока за исключением об-менно-корреляционной части

[]∫∫∇==.)(),(drrrVdrVEXCXCXCβαβαχρρχχχ

Так как сам функционал VXC сложным образом зависит от переменной интегрирования (через электронную плотность), найти этот интеграл можно только численно. Для этого выбирается пространственная сетка интегри-рования. Обычно выбирают 1000 – 30000 точек интегрирования на каждый атом.

Рассмотрим размеры сетки интегрирования на примере наиболее из-вестных квантовохимических программ. По умолчанию в программе Gaus-sian сетка интегрирования (75, 302), т.е. она состоит из 75 радиальных оболо-чек с 302 угловыми точками на каждую оболочку. В программе GAMESS сетка похуже (63, 302), однако, она может настраиваться более тонким обра-зом, чем в программе Gaussian (например, для каждого типа атомов может быть выбрана своя сетка интегрирования).

Очевидно, чем больше сетка, т.е. меньше шаг интегрирования, тем точ-нее результат численного интегрирования. Поэтому энергия молекулы в ме-тодах DFT в принципе зависит от выбора сетки, и сравнивать энергии раз-личных систем можно только при идентичных сетках! Сетка для EXC играет такую же роль, как базис для остальных вкладов энергии в Etotal. Более того, несовершенство сетки может приводить к ошибкам суперпозиции сеток (grid superposition error) аналогично ошибкам суперпозиции базисных наборов для несовершенных базисов.

10

15.8. Качество расчета методов функционала плотности.

Как уже отмечалось выше, качество лучших DFT методов сравнимо с качеством расчетов самыми сложными пост-хартри-фоковскими приближе-ниями. В таблице приведены средняя ошибка Δср и максимальное отклонение Δmax (в ккал/моль) результатов расчета энтальпий образования, потенциалов ионизации и некоторых других энергетических характеристик тестового G2-набора химических соединений. Видно, что метод Хартри-Фока характеризу-ется неудовлетворительно большими погрешностями, причем ситуацию не исправляет улучшение базисного набора. Локальный DFT метод SVWN зна-чительно улучшает соответствие расчета эксперименту, однако, погрешность расчета остается достаточно высокой. Лучшие результаты показывает метод теории возмущений MP2. Использование гибридного функционала даже со сравнительно простым базисным набором 6-31G(d) дает результаты не хуже результатов MP2 расчетов со сложным базисом. А улучшение базисного на-бора позволяет еще заметно снизить погрешность расчета, доведя ее всего до 3.1 ккал/моль!

Лучшие DFT методы хорошо воспроизводят распределение электронной плотности по молекуле. Ниже приведены дипольные моменты (в Дебаях) не-которых соединений, рассчитанные различными приближениями с использо-ванием базиса DZ-качества. Видно улучшение качества расчета в таблице слева направо. Так, DFT метод с градиентной коррекцией BLYP показывает лучшие результаты, чем HF и MP2, особенно для проблемных случаев (моле-кула CO). Гибридный функционал B3LYP обеспечивает прекрасное соответ-ствие расчета эксперименту.

11

В заключение рассмотрим вопрос, являются ли методы DFT полуэмпи-рическими или ab initio методами?

Если ab initio означает отсутствие эмпирических параметров, подобран-ных для соответствия расчетных характеристик экспериментальным, то не-которые разновидности DFT являются ab initio, а некоторые – нет. Однако, число этих параметров значительно меньше, чем в традиционных полуэмпи-рических методах. Например, PM3 метод использует по 18 подобранных па-раметров для каждого атома Периодической таблицы, тогда как В88 обмен-ный функционал включает только одну подобранную константу, используе-мую для всей Периодической таблицы.

Если ab initio означает, что данный метод в принципе способен дать точный результат, то DFT методы, безусловно, являются ab initio методами. При условии использования совершенного базисного набора единственной проблемой DFT методов является неизвестная форма функционала для рас-чета корреляционно-обменной энергии.

Наконец, DFT методы характеризуются исключительно высо-кой точностью, совершенно недоступной даже для лучших полуэм-пирических методов (MNDO, AM1, PM3) и сопоставимой с точно-стью весьма сложных ab initio методов, основанных на использова-нии теории возмущений и конфигурационного взаимодействия.__

http://www.qchem.ru/d/lect/khsl_qchem/16Lecture-15.pdf

Теория функционала плотности (англ. density functional theory, DFT) — метод расчёта электронной структуры систем многих частиц в квантовой физике и квантовой химии. В частности, применяется для расчёта электронной структуры молекул и конденсированного вещества. Является одним из наиболее широко используемых и универсальных методов в вычислительной физике и вычислительной химии.

Модель Томаса — Ферми[править | править вики-текст]

Основная статья: Теория Томаса — Ферми

Методу теории функционала плотности предшествовала модель Томаса — Ферми, развитая Л. Томасом и Энрико Ферми в 1927 г. Они рассчитали энергию атома как сумму его кинетической энергии, представленной в видефункционала электронной плотности, и потенциальной энергии взаимодействия электронов с ядром и друг с другом; энергия взаимодействия также была выражена через электронную плотность.

Несмотря на заметную роль, которую модель Томаса — Ферми сыграла в развитии квантовой механики, её точность была недостаточной, поскольку не учитывалось обменное взаимодействие, в отличие, например, отметода Хартри — Фока. В 1928 г. Поль Дирак уточнил функционал энергии в модели Томаса — Ферми, добавив к нему слагаемое, описывающее обменное взаимодействие (это слагаемое также имело вид функционала электронной плотности).

Несмотря на это, для ряда применений модель Томаса — Ферми — Дирака не давала удовлетворительного результата. Основным источником погрешности являлось выражение кинетической энергии, приводящее к погрешности в вычислении обменной энергии. Кроме того, не учитывалась энергия электронной корреляции.

Теоремы Хоэнберга — Кона[править | править вики-текст]

Хотя теория функционала плотности и базируется на ставшей классической модели Томаса — Ферми, надёжное теоретическое обоснование под нее было подведено только с формулировкой теорем Хоэнберга — Кона(названных так в честь Пьера Хоэнберга (англ.) и Уолтера Кона).

Первая теорема утверждает, что существует взаимно однозначное соответствие между плотностью основного состояния электронной подсистемы, находящейся во внешнем потенциале атомных ядер, и самим потенциалом ядер. Первая теорема является теоремой существования и не дает метода построения такого соответствия.

Вторая теорема представляет собой вариационный принцип квантовой механики, сформулированный для функционала плотности и утверждает, что энергия электронной подсистемы, записанная как функционал электронной плотности, имеет минимум, равный энергии основного состояния.

Первоначально теоремы Хоэнберга — Кона были сформулированы только для основного состояния электронной подсистемы в отсутствие магнитного поля. Они могут быть обобщены путём введения зависимости от времени, что позволяет использовать этот формализм для расчета состояний возбуждённых электронов^[1].

Описание метода[править | править вики-текст]

Традиционные методы определения электронной структуры, в частности, метод Хартри — Фока и производные от него, описывают систему с помощью многоэлектронной волновой функции. Основная цель теории функционала плотности — при описании электронной подсистемы заменить многоэлектронную волновую функцию электронной плотностью. Это ведет к существенному упрощению задачи, поскольку многоэлектронная волновая функция зависит от   переменных — по 3 пространственных координаты на каждый из   электронов, в то время как плотность — функция лишь трёх пространственных координат.

Как правило, метод теории функционала плотности используется совместно с формализмом Кона — Шэма, в рамках которого трудноразрешимая задача об описании нескольких взаимодействующих электронов в статическом внешнем поле (атомных ядер) сводится к более простой задаче о независимых электронах, которые движутся в некотором эффективном потенциале. Этот эффективный потенциал включает в себя статический потенциал атомных ядер, а также учитывает кулоновские эффекты, в частности, обменное взаимодействие и электронную корреляцию.

Описание двух последних взаимодействий и представляет собой основную сложность метода теории функционала плотности в формулировке Кона — Шэма. Простейшим приближением здесь является приближение локальной плотности, основанное на точном расчёте обменной энергии для пространственно однородного электронного газа, который может быть выполнен в рамках модели Томаса — Ферми и из которого можно получить также и корреляционную энергию электронного газа.

Метод теории функционала плотности широко применяется для расчётов в физике твёрдого тела с 1970-х годов. В ряде случаев даже использование простого приближения локальной плотности дает удовлетворительные результаты, соответствующие экспериментальным данным, причём вычислительная сложность метода невысока относительно других подходов к проблеме многих частиц в квантовой механике. Тем не менее, долгое время метод был недостаточно точен для расчётов в области квантовой химии, пока в 1990-х годах не произошёл заметный сдвиг в описании обменного и корреляционного взаимодействий. В настоящее время метод теории функционала плотности является главным подходом в обеих областях. Впрочем, несмотря на прогресс в теории, все ещё имеются проблемы в приложении метода к описанию межмолекулярных сил, в особенности Ван-дер-Ваальсовых сил и дисперсионного взаимодействия, а также в расчётах ширины запрещённой зоны в полупроводниках.

Сложности с расчётом дисперсионного взаимодействия в рамках теории функционала плотности (которые возникают, как минимум, в том случае, когда этот метод не дополняется другими) делают метод теории функционала плотности малопригодным для систем, в которых дисперсионные силы являются преобладающими (например, при рассмотрении взаимодействия между атомами благородных газов) или систем, в которых дисперсионные силы имеют тот же порядок, что и другие взаимодействия (например, в органических молекулах). Решение этой проблемы является предметом современных исследований.

Формальное обоснование метода[править | править вики-текст]

Согласно приближению Борна — Оппенгеймера, которое применяется в большинстве расчётов электронной структуры, ядра, входящие в состав рассматриваемой системы, считаются неподвижными. Электростатический потенциал  , создаваемый этими «неподвижными» ядрами, является внешним для электронов. Стационарное состояние электронов описывается волновой функцией  , которая является решением уравнения Шрёдингера

где   — гамильтониан электронной подсистемы,   — количество электронов,   описывает электрон-электронное взаимодействие. Операторы   и   одинаковы для всех систем, в то время как вид   зависит от конкретной системы. Как видно, основное отличие одночастичной задачи от задачи многих тел состоит в наличии слагаемого, описывающего электрон-электронное взаимодействие,  . Существует большое количество методов решения многочастичного уравнения Шрёдингера, основанных на разложении волновой функции с использованиемопределителя Слэтера. Простейший из них — метод Хартри — Фока, на основе которого развит ряд современных методов. Общей проблемой для них является значительная вычислительная трудоёмкость, из-за которой область применения метода Хартри — Фока и производных от него ограничена не слишком большими системами.

Метод теории функционала плотности в значительной степени решает проблему расчёта систем, включающих большое число частиц, путём сведения задачи о системе многих тел с потенциалом электрон-электронного взаимодействия   к одночастичной задаче, в которой слагаемое   отсутствует.

Плотность частиц,  , с помощью которой и строится формализм теории функционала плотности, задается выражением:

Хоэнберг и Кон в 1964 показали^[2], что это выражение может быть обращено: по заданной плотности частиц в основном состоянии,  , можно найти соответствующую волновую функцию основного состояния  . Иными словами,   — единственный функционал от  , то есть

а, следовательно, все остальные наблюдаемые физические величины   также являются функционалами  :

В частности, для энергии основного состояния можно записать

где вклад внешнего потенциала   может быть переписан через плотность частиц:

Функционалы   и   одинаковы для всех систем, а  , очевидно, зависит от вида рассматриваемой системы. Для заданной системы вид   известен, и можно минимизировать функционал

относительно распределения плотности частиц  , если, конечно, имеются выражения для   и  . В результате минимизации получается плотность частиц в основном состоянии  , а вместе с ней и все наблюдаемые в основном состоянии величины.

Вариационная задача отыскания минимума функционала энергии   может быть решена с помощью метода множителей Лагранжа, как это и было сделано Коном и Шэмом в 1965 г^[3]. Таким образом, функционал энергии в приведённом выше выражении может быть записан как эффективный функционал плотности частиц в одночастичной системе:

где   означает кинетическую энергию свободной частицы, а   — эффективный внешний потенциал для электронной подсистемы. Ясно, что   если   взят в виде

Решение так называемых уравнений Кона — Шэма для вспомогательной системы, из которой исключено электрон-электронное взаимодействие,

даёт орбитали  , по которым восстанавливается электронная плотность   исходной многочастичной системы:

Эффективный одночастичный потенциал   записывается как

где второе слагаемое — слагаемое Хартри — описывает электрон-электронное кулоновское отталкивание, а последнее слагаемое   называется обменно-корреляционным потенциалом. Здесь   включает все многочастичные взаимодействия.

Поскольку слагаемое Хартри и член   зависят от плотности  , которая зависит от  , которая, в свою очередь, зависит от  , решение самосогласованных уравнений Кона — Шэма может быть произведено с помощью итеративной процедуры последовательных приближений. Как правило, отталкиваясь от начального приближения для  , рассчитывается соответствующее слагаемое  , для которого затем решаются уравнения Кона — Шэма, из которых получается  . Отсюда можно получить следующее приближение для плотности и т. д.

Приближения[править | править вики-текст]

Основная проблема, связанная с методом теории функционала плотности заключается в том, что точные аналитические выражения для функционалов обменной и корреляционной энергии известны только для частного случая газа свободных электронов. Тем не менее, существующие приближения позволяют рассчитать ряд физических величин с достаточной точностью. В физических приложениях наиболее распространено приближение локальной плотности (LDA), в котором принято, что функционал, вычисляемый для некоторой точки пространства, зависит только от плотности в этой точке:

Приближение локальной спиновой плотности (LSDA) является непосредственным обобщением приближения локальной плотности, учитывающим спин электрона:

Достаточно точное выражение для плотности обменно-корреляционной энергии   было получено с помощью квантового метода Монте-Карло при расчётах газа свободных электронов.

Метод обобщённого градиентного приближения (GGA) также является локальным, но, в отличие от метода локальной плотности, учитывает градиент плотности в точке рассмотрения:

Использование этого приближения дает хорошие результаты при расчете геометрии и энергии основного состояния молекул.

Существуют и более точные приближения, которые в значительной степени позволяют решить проблему вычисления функционала обменно-корреляционной энергии.

Обобщение на случай магнитного поля[править | править вики-текст]

Формализм метода теории функционала плотности нарушается в условиях наличия векторного потенциала, в частности, в присутствии магнитного поля. В этом случае не существует взаимно однозначного соответствия между электронной плотностью и внешним потенциалом (атомных ядер). Попытки обобщения формализма для учёта эффектов, связанных с магнитным полем, вылились в две разных теории: в теорию функционала плотности с учётом вектора плотности тока, и в теорию функционала плотности с учётом магнитного поля. В обоих случаях функционал обменно-корреляционной энергии обобщается и становится зависящим не только от электронной плотности. В первом подходе, развитом Vignale и Rasolt, помимо электронной плотности, аргументом является ещё и плотность тока. Во втором подходе (Salsbury, Grayce, Harris) дополнительным аргументом функционала служит магнитное поле, и вид функционала зависит от вида магнитного поля. Для обоих методов вычисление обменно-корреляционной энергии за рамками приближения локальной плотности (вернее, его обобщения на случай магнитного поля) оказалось весьма сложным.

Применения[править | править вики-текст]

На практике, метод Кона — Шэма может быть применён несколькими различными способами, в зависимости от цели исследования. В расчётах для физики твёрдого тела до сих пор широко используется приближение локальной плотности, вкупе с базисом плоских волн. Для расчётов электронной структуры молекул требуются более сложные выражения для функционалов. Так, большое число приближенных функционалов для расчёта обменно-корреляционного взаимодействия было развито для задач химии. Некоторые из них противоречат приближению пространственно однородного электронного газа, но тем не менее, в пределе при переходе к электронному газу должны сводиться к приближению локальной плотности.

Для расчётов физических задач наиболее часто применяется, по-видимому, уточнённая обменная модель Perdew — Burke — Ernzerhof, однако известно, что она приводит к ошибкам в калориметрических параметрах, будучи приложенной к расчётам молекул в газовой фазе.

В расчётах квантовой химии одним из распространённых является вид обменного функционала, называемый BLYP (Becke, Lee, Yang, Parr). Еще более широко распространено приближение B3LYP^[4][5][6], которое основано на гибридном функционале, в котором обменная энергия рассчитывается с привлечением точного результата, полученного методом Хартри — Фока.

В целом, текущее состояние метода теории функционала плотности таково, что невозможно оценить погрешность расчёта, не сравнивая его результаты с другими подходами или с результатами экспериментов.

Азобензол C6H5N=NC6H5 — простейшее ароматическое азосоединение.

Свойства

Оранжево-красные кристаллы. Устойчив транс-изомер, температура плавления 68 °C, нерастворим в воде, растворяется в эфире, ледяной уксусной и концентрированной серной кислотах. Азобензол не удерживается волокнами и сам по себе не является текстильным красителем. Он проявляет свойства жирорастворимого красителя и может быть использован для окраски технических жидкостей. Если в молекулу азобензола ввести амино- или оксигруппы, то цвет таких азокрасителей изменится с оранжево-красного до красного, при введении гидроксигрупп, до красного. Азобензол восстанавливается до анилина через гидразобензол, как установлено Н.Н. Зининым в 1845. Замещенные азобензолы обычно получают реакцией азосочетания диазсоединений, полученных диазотированием ароматических аминов и фенолов или ароматических аминов.

Оптические свойства[править вики-текст]

Переход азобензола из одной формы в другую при облучении видимым и УФ излучением

Азобензол имеет два изомера: цис- и транс-форму. Поскольку в цис-изомере два атома водорода из разных фенильных колец оказываются в одном и том же месте, их отталкивание приводит к скручиванию молекулы и разрушению единой системы обобществлённых π-орбиталей. В транс-изомере такого конфликта не происходит, и образуется единая система из семи сопряжённых π-связей. В результате цис-изомер вещества бесцветен и менее устойчив, а транс-изомер окрашен (имеет полосу поглощения в синей части спектра).

Облучение ультрафиолетом приводит к образованию цис-изомера и обесцвечиванию вещества; облучение синим светом или нагревание приводят к получению транс-изомера и появлению окраски.

Получение[править вики-текст]

Азобензол получают восстановлением нитробензола в щелочном растворе цинковой пылью или электрохимическим методом. Кроме того, его можно получать восстановлением нитробензола амальгамой натрия или алюмогидридом ли, окислением гидразобензола гипобромитом натрия или конденсацией нитрозобензола с анилином в уксусной кислоте (применяется для синтеза асимметричных азобензолов).

Қорытынды

Химиялық құбылыстар мен үрдістерді атомдық-молекулалық деңгейде зерттеу кезінде квантты-химиялық заңдар қолданылады. Кванттық механика химиялық қосылыстардың көптеген қасиеттерін, сонымен қатар классикалық теориямен анықталмайтын қасиеттерін түсіндіру мен алдын-ала болжауға мүмкіндік береді.

Қазіргі кезде көптеген ғылыми зерттеу қоғамдары сұйық кристалдардың жаңа түрлерін ашып, зерттеуге және олардың іс жүзінде қажетті қасиеттерін тауып, пайдалануға қызығушылық танытуда. Сұйық кристалдар — қайсыбір температурада молекулалары белгілі бір тәртіппен орналасуы нәтижесінде қатты кристалдарға тән кейбір физикалық қасиеттердің анизатропиясы болатын сұйықтар. Тәртіптеу типіне қарай сұйық кристалдар нематикалық, смектикалық және холестерикалық болып бөлінеді. Нематикалық сұйық кристалдар сыртқы әсер жоқ кезде тек бағытталған тәртіптілікпен және барлық көлем бойынша молекулалардың бірқалыпты ориентациясымен сипатталады. Смектикалық сұйық кристалдар бағытталған тәртіптілікпен қатар белгілі трансляциялық тәртіптілік түрімен сипатталады. Холестерикалық сұйық кристалдар да басты ориентация бағыты молекулалық өзара әрекет салдарынан спираль секілді оралған. Сыртқы электр өрісіндегі жұқа қабаты сұйық кристалдар қайта бағыт-бағдарлануынан оптикалық қасиеттерінің өзгеруін, яғни электроптикалық құбылысты, электроникада бейнелену және ақпаратты оптикалық түрде өңдеу құрылғыларында жиі пайдаланады. Осы мақсатта сұйық кристалдардың жаңа перспективті түрлерін алу үшін зерттеу жұмыстары жүргізілуде. Дегенмен, қажетті ақпаратты тәжірибелік жолмен алу үшін көптеген реакцияларды әр түрлі деңгейде жүретін үрдістерде өткізу қажет болады. Ал бұл өз кезегінде ұзақ уақытты, материалдық шығынды қажет етеді. Мұндай тиімсіз әрекеттерге жол бермес үшін математикалық модельдеу кезінде алғашқы сатылардың бірі болып квантты-химиялық есептеулер табылады.

Квантты химияның есептеу әдістері мен тез әрекет ететін ЭЕМ (электронды есептеуіш машиналары) дамуы органикалық қосылыстардың әр түрлі сипаттамаларын, сонымен қатар тұрақты емес ауыспалы жағдайларын анықтауға мүмкіндік береді. Бұл есептеулердің нақтылығы термохимиялық тұрақтылармен сәйкес келеді. Сол себепті квантты-химиялық есептеулер қазір күрделі органикалық реакциялардың механизмін анықтап есептеуде кеңінен қолданылады және маңызы зор.

Соңғы жылдары бұл салада өте үлкен даму болды. Квантты химияның өте жоғары деңгейде дамуының арқасында молекулалық орбитальдер әдістерінің жартылай эмпирикалық және эмпирикалық емес түрлері дамытылған. Олар тек қана органикалық химияда емес, биохимияда да маңызы зор. Осы әдістер көмегімен реакция өнімдерінің шығымына қандай факторлар әсер ететінін, сонымен бірге тәжірибе үшін қол жетімсіз геометриясы мен электрондық құрылымы туралы ақпарат алуға болады.

Кез-келген заттың молекуласын қарастырған кезде біз оған жанындағы басқа молекулалардың әсерін қарастыра қоймаймыз. Шынайы заттар жалғыз молекуладан тұрмайтын болғандықтан, ол заттың барлық қасиетін аша алмайтыны түсінікті. Себебі жанындағы өзге молекуланың әсерінен бастапқы молекула да, жанындағы молекула да құрылысын, жалпы заттың физика-химиялық қасиеттерін өзгертеді. Және де ол молекулалар қатып қалған күйінде емес, әрдайым қозғалыста болатыны белгілі.

Біз зерттеуге алған пара-орынбасылған фенилпропаргилоксибензол молекулаларының және осылардан құралған димер молекулаларының есептеулерін GAUSSIAN 03 эмпирикалық емес жуықтауында есептедік. Есептеуге жіберер алдында димердегі молекулалардың өзара орналасуын СhemBio3D Ultra 11.0 бағдарламасы арқылы орындадық (қосымшаларда көрсетілген).

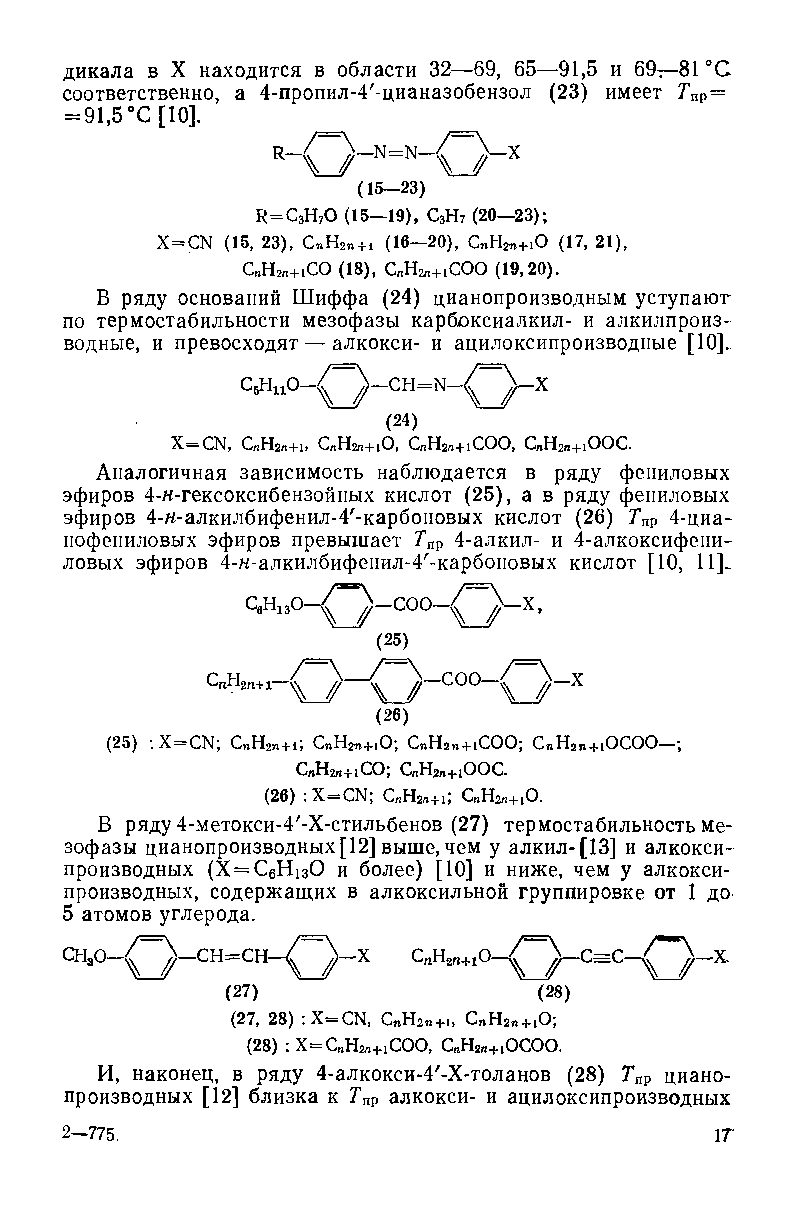
Пара- (мұндағы Х CN және NO₂ топтары), яғни электронакцепторлы топтармен пара-орынбасылған фенилпропаргилоксибензол молекулаларынан құралған димерлерге жүргізілген квантты-химиялық есептеулер көмегімен алынған нәтижелер келесідей:

1. CN және NO₂ электронакцепторлы топтарымен пара-орынбасылған фенилпропаргилоксибензолдардың параллель жағдайда орналасқан димерлері тәжірибелік тұрғыда әлі зерттелмеген. Олардың физикалық қасиеттері молекулалардың өзара орналасуына тікелей байланысты. Х осінде молекулалар өзара «басы-соңына» орналастырылып салынған димерлердің екеуі де оны құрайтын молекулалардың конформациясының сақталуымен түзілді және бұл димер молекулалары қалған басқаларымен салыстырғанда ең тұрақты болып саналды.

2. Х осінде молекулалар өзара «соңы-соңына» орналастырылып салынған димерлердің арақашықтығы өте үлкен, яғни молекулалардағы аттас зарядтар тебілген. CN орынбасылған ФПОБ димерінде 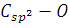байланысы төңірегінде айналу байқалды және басқа Х осімен параллель орналастырылған қалған екі өзі аттас димерден түзілу энергиясы көбірек, яғни тұрақтылығы салыстырмалы түрде аз. Ал, нитротобы бар димер бұл орналастыруда өз конформациясын сақтаған.

3. Х осі бойымен «басы-басына» орналастырылған димердің жекелеген молекулаларының да арақашықтығы аттас зарядтардың әсерінен өте үлкен. Аталып отырған екі түрлі димерлердің жекелеген молекулаларының конформациялары сақталған.

4. Ү осі бойымен оттек атомдары қарама-қарсы екі жақта орналасқан молекулалардан құрастырылған CN-орынбасылған ФПОБ димерінің геометриялық конфигурациясы оттек атомдары жақындатылып орналасқанына қарағанда көбірек өзгеріп, сызықтық конформациясын сақтамаған. Осыған сәйкесінше біріншісінің түзілу энергиясы екіншісімен салыстырғанда көбірек, яғни тұрақсыз.

5. Ал NO₂ орынбасылған ФПОБ молекулаларын бір-біріне антипараллель (біріншісінде - оттек атомдарын қарама-қарсы екі жақта, екіншісінде - бір-біріне жақындатып) орналастырып димер құрастырғанда, бірінші димерді құрайтын екі молекуланың геометриялық конфигурациясы өзгеше болды: екі молекула да сызықтылығын сақтаған, тек біреуі байланысы төңірегінде айналу бұрышын өзгерткен. Ал, екінші димер молекулалары бастапқы пішінін өзгертпеген десек те болады. Бірінші димердің түзілуіне азырақ энергия қажет болған.

6. Z осі бойымен антипараллель орналастырылған CN және NO₂ электронакцепторлы топтарымен пара-орынбасылған фенилпропаргилоксибензол димер молекулаларының сызықты конформациясы бұзылған, екінші димерде бұл өзгеріс анық байқалады. Себебі, бастапқы NO₂ орынбасылған ФПОБ молекуласы жазық конформациялы болатын, екі жазық молекуланы антипараллель беттестіріп орналастырғанда зарядтардың өзара әсерлесуі күшті болады.

Әрбір CN және NO₂ электронакцепторлы топтарымен пара-орынбасылған фенилпропаргилоксибензол молекулаларын 6 түрде (3 рет қатарынан, 3 рет антипараллель) орналастырып димер молекуласын құрастырып көргенде, өзара «басы-соңына» орналасқан димер энергиялық жағынан да тиімді екеніне, бастапқы геометриялық конфигурациясын сақтайтынына да көз жеткіздік.

Фенилпропаргилоксибензол молекулалары үшін сызықты конформациясын сақтауы ( байланысы төңірегінде айналу мұндай пішінге әсер етпейді) өте маңызды. Себебі, нематик молекулалар үшін сызықты пішіннің жойылуы оның мезогендік қасиеттеріне кері әсер етеді, байланысы бойымен айналу осыған алып келеді. Келесі димерлер молекулаларында сызықтылық сақталмаған: пара-CN-орынбасылған ФПОБ димері үшін Ү осі бойымен (екі молекуланың оттек атомдары қарама-қарсы) антипараллель орналасқаны және Z осі бойымен антипараллель орналасқаны, ал пара- NO₂ -орынбасылған ФПОБ димері үшін тек Z осі бойымен антипараллель орналасқаны.

Теориялық квантты-химиялық әдістерді сұйық кристалды қосылыстардың димерлерінің геометриялық конфигурациялары мен қасиеттерін зерттеуде қолдану электрондық деңгейде есептеу жүргізіп физикалық қасиеттерін ұғынуға және оларға қатысты маңызды мәліметтер алуға мүмкіндік берді.