14.Методи, що використовуються для розв’язування задач
багатокритеріального програмування.
Для розв’язування задач лінійного програмування з декількома цільовими функціями найчастіше використовують такі методи:
- метод вагових коефіцієнтів;
- метод пріоритетів;
- метод мінімізації загальної поступки.
Ці методи є різними і в загальному випадку дають розв’язки, що не співпадають між собою. Не можна вважати, що один з методів є кращим за інші; по суті наведені методи призначені для розв’язування задач з різними перевагами в процесі прийняття рішень.
15.Характеристика методу вагових коефіцієнтів.
В методі вагових коефіцієнтів єдина цільова функція формується як зважена сума вихідних цільових функцій. Припустимо, що в моделі є n цільових функцій Fi, з яких k потрібно максимізувати, а інші – мінімізувати. Нехай – wi додатній ваговий коефіцієнт, який відображає важливість кожної цільової функції, причому Σ wi=1
Узагальнена цільова функція записується так:
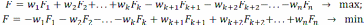
16.Характеристика методу пріоритетів.
В методі пріоритетів цільовим функціям Fi вихідної задачі присвоюється ранг, який вказує на важливість цільової функції. В методі пріоритетів почергово розв’язуються задачі з однією цільовою функцією, починаючи з функції з найбільшим пріоритетом, і завершуючи функцією, пріоритет якої найнижчий. В процесі розв’язування послідовних задач розв’язок задачі, що має нижчий пріоритет, може погіршити отримане раніше значення задач з цільовою функцією з вищим пріоритетом лише на заздалегідь встановлену величину δ. Тобто, на будь-якому етапі при розв’язку задачі лінійного програмування з’являється (i-1) додаткових обмежень.
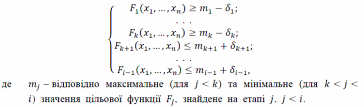
17.Характеристика методу мінімізації загальної поступки.
В методі мінімізації загальної поступки розв’язуються n задач лінійного програмування з кожною цільовою функцією та визначаються оптимальні значення кожної цільової функції. Потім вводиться загальна відносна поступка z, задаються коефіцієнти цільових функцій gi та формулюється задача мінімізації поступки за z обмежень:
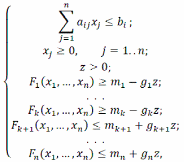
В наведеній моделі замість параметрів gi можна використовувати знайдені оптимальні значення mi