Рівень 1 (2 бали, 3 питання).
1. Фігура, що складається з вершин та ребер називається: а) графом;
2. Якщо існують шляхи, що з’єднують будь-які дві вершини графа,
то граф називається: б) зв’язаним;
3. Якщо ребра графа асоціюються з певними числами, то граф
називається: в) мережею.
4. Кістякове дерево – це:
а) зв’язаний граф, що містить підмножину вершин початкового
графа і не містить циклів;
5. Для розв’язування задач пошуку найкоротшого шляху
використовують:
в) обидві відповіді вірні. (алгоритм Флойда+ алгоритм Дійкстри)
6. У мережевих задачах обмеження для вузлів виражає:
в) баланс потоку, що проходить через вузол.
7. В орієнтованих дугах невід’ємний потік можливий:
в) лише в одному напрямку.
8. В задачі про максимальний потік максимізується:
а) потік від початкової вершини до кінцевої;
9. Для розв’язування задачі про максимальний потік
використовується:
а) алгоритм Форда і Фалкерсона;
10. У мережевих задачах обмеження для дуг задає, що:
в) обидві відповіді вірні. (потік по дузі не перевищує верхньої межі пропускної здатності+ потік по дузі є не меншим нижньої межі пропускної
здатності)
11. Задача, розв’язок якої повинен задовольнити декілька цільових
функцій, називається:
б) задачею багатокритеріального програмування;
12. Розв’язок задачі багатокритеріального програмування називається:
в) ефективним.
13. Для розв’язування задачі багатокритеріального програмування
використовують:
а) метод пріоритетів;
14. Для розв’язування задачі багатокритеріального програмування
використовують:
в) обидві відповіді вірні ( метод пріоритетів +метод вагових коефіцієнтів)
15. Розв’язки, отримані різними методами розв’язування задач
багатокритеріального програмування:
б) як правило, не співпадають між собою;
16. При використанні методу вагових коефіцієнтів єдина цільова
функція формується як:
б) зважена сума вихідних цільових функцій;
17. Сума вагових коефіцієнтів, що показують важливість кожної
цільової функції, дорівнює:
б) одиниці;
18. У методі пріоритетів спочатку розв’язуються задача з цільовою
функцією, пріоритет якої:
а) найбільший;
19. У методі пріоритетів розв’язок задачі з цільовою функцією, що
має нижчий пріоритет:
а) може погіршити отримане раніше значення;
20. У методі мінімізації загальної поступки вводиться:
б) загальна відносна поступка;
Рівень 2 (4 бали, 3 питання).
1. Дати означення поняттям «граф», «шлях», «дерево».
Граф – фігура, яка складається з точок (вершин) сполучених лініями (ребрами)
Шляхом, що з’єднує вершини A і B, називається сукупність ребер, початком першого з яких є вершина A, а кінцем останнього – вершина B
Деревом називається зв’язаний граф, що містить підмножину вершин вихідного графа і не містить циклів
2. Приклади задач, які можна подати у вигляді мережевих моделей.
Прикладом задач, які можна подати у вигляді мережевих моделей є: - проектування найкоротшого газопроводу, що з’єднує морські бурові свердловини з приймальною станцією на березі; - пошук найкоротшого маршруту між двома пунктами по існуючій мережі; - визначення максимальної пропускної здатності вулично-дорожньої мережі, що з’єднує райони міста; - визначення схеми транспортування нафти від свердловин до нафтопереробних заводів з мінімальною вартістю транспортування; - складання часового графіка виконання робіт (визначення дат початку і закінчення окремих етапів робіт).
3. Побудувати мінімальне кістякове дерево для графа, наведеного на
рисунку (3 ітерації).
4. Побудувати мінімальне кістякове дерево для графа, наведеного на
рисунку (3 ітерації).
5. Формалізація задачі пошуку найкоротшого шляху як задачі
лінійного програмування.
Нехай мережа складається з n вузлів і потрібно знайти найкоротший шлях між двома вузлами s і t цієї мережі.
Припустимо, що у вузол s входить одиниця зовнішнього потоку, і цей потік виходить через вузол .t Позначимо
Xij– величина потоку, що проходить по дузі (i, j);
Cij – довжина дуги (i, j);
Оскільки лише одна одиниця потоку може пройти через будь-яку дугу в кожен момент часу, то змінні Xij можуть приймати значення 0 або 1. При цих позначеннях цільову функцію, яку потрібно мінімізувати:
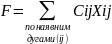
Для кожного вузла визначається лише одне обмеження, що задає баланс потоку, який проходить через даний вузол:
загальний вхідний потік = загальний вихідний потік.
Варто відзначити, що одне обмеження завжди є зайвим, тобто будь-яке обмеження можна отримати з інших n-1 обмежень.
6. Використання задачі пошуку найкоротшого шляху для
розв’язування задачі про заміну обладнання.
7. Розв’язування задачі про найбільш надійний маршрут (ваги дуг –
імовірність беззупинкового проїзду).
На рис. 9.2 наведено схему мережі вулиць, якими пан Петренко щоденно їздить автомобілем з дому на роботу. Дана ділянка вулично- дорожньої мережі посилено контролюється нарядами ДАІ, і автомобіль Петренка часто зупиняють за перевищення швидкості. Тому пан Петренко планує розробити маршрут, на якому він би мав найбільшу ймовірність не бути зупиненим інспекторами ДАІ. Імовірність проїзду без зупинки для кожної вулиці наведено на схемі (рис. 9.2).
Імовірність не бути зупиненим на маршруті 1 — 2—…— m дорівнює добутку ймовірностей не бути зупиненим на кожній ділянці мережі, тобто
p1,m= p12 * p2j * …* pjm
Цю задачу можна звести до задачі пошуку найкоротшого шляху, якщо замість ймовірностей використовувати їх логарифм, тоді добуток ймовірностей перетвориться в суму логарифмів ймовірностей
lnp1m= lnp12 * lnp2j * …*lnpjm
Задача ймовірності p1,m еквівалентна формулі максимізації задачі величини lnp1m оскільки p1,m ≤1 відповідно lnp1m ≤ 0
Таким чином задача максимізації логарифму lnp1m еквівалентна задачі мінімізації величини (- lnp1m). Замінивши імовірності pij на величини (- lnpij) отримаємо мережу до якої можна застосувати алгоритм пошуку найкоротшого шляху.
Для цієї нової мережі найкоротшим шляхом є шлях 1→3→5→7 з довжиною - lnp1,7 =1,1707 Тоді максимальна ймовірність не бути зупиненим становить p1,7 =0,0675.