
Vorob'evaEA.Vorob'evaEV_Lineinaya__algebra,Vectornaya_algebra,Analit_geometriya
.pdf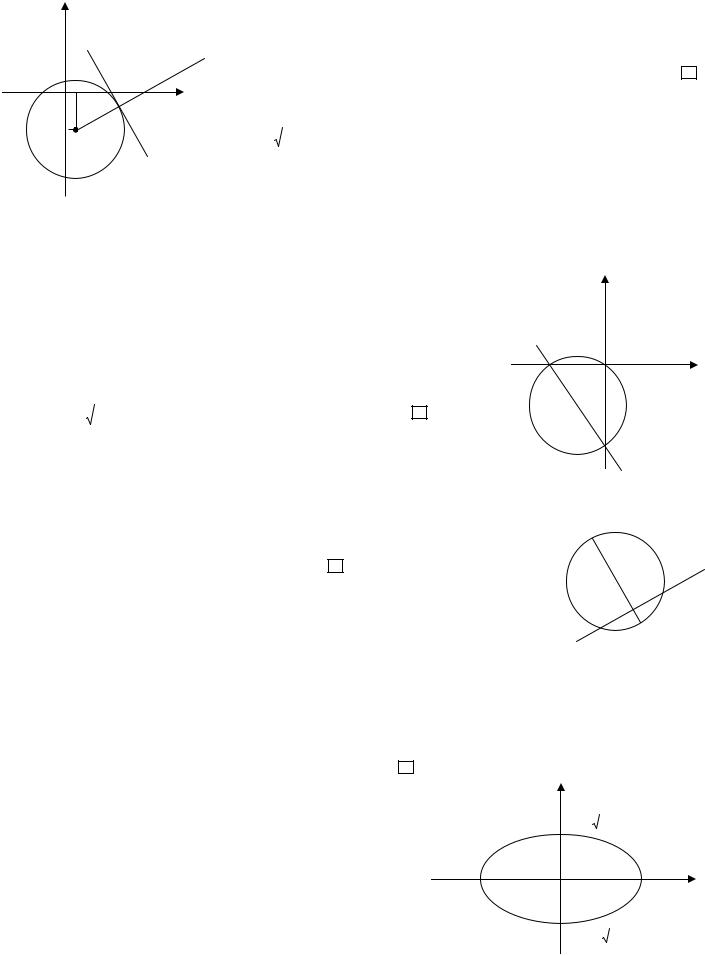
y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. BM – кратчайшее расстояние от точки |
B до окружности. |
Очевидно, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BM = BC − CM . |
|
C (a, b) |
– |
центр окружности, |
|
|
CM - |
ее |
|
|
радиус. |
Приведем |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(7,6) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение окружности к каноническому виду (x2 - 2x +1)+ (y 2 + 4 y + 4)= 25 |
2 или |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x -1)2 + (y + 2)2 = 52 |
C (1, - 2), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
R = 5 . |
Вычислим |
|
|
|
|
длину |
отрезка |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC = |
|
|
|
|
|
|
|
= 10 . BM = BC − CM = 10 − 5 = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1- 7)2 + (- 2 - 6)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C (1,−2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: BM = 5 . |
||||||||
|
|
|
|
|
|
Задача 5. |
|
|
Составить уравнение окружности, диаметром которой является отрезок |
|
прямой 12x + 5 y + 60 = 0 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
заключенный между осями координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Решение. Преобразуем уравнение |
прямой 12x + 5 y + 60 = 0 к |
|
виду «уравнение |
прямой |
в |
|
отрезках |
на |
осях»: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
y |
|
|
|
|
= 1 , откуда видно, что A(- 5, 0) - |
B(0, -12) и точки пересечения прямой с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
- 5 |
|
-12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
осями координат, AB - диаметр окружности по условию задачи. |
Следовательно, центр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
окружности - точка C – |
середина AB , т.е. координаты центра окружности |
|
C(- 2,5; - 6) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ведь xC |
|
= |
|
xA + xB |
, |
yC = |
y A + yB |
, а радиус окружности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
×13 = 6,5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
R = |
|
AB |
|
|
= |
|
(- 5)2 + (-12)2 |
|
Уравнение окружности по 2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(x + 2,5)2 + (y + 6)2 = 6,52 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (x + 2,5)2 + (y + 6)2 = 6,52 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
Задача 6. |
|
|
|
|
|
Окружность |
|
задана уравнением |
|
x2 + y 2 - 6x +14 y - 6 = 0 . |
Составить |
|
уравнение |
ее |
диаметра, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
перпендикулярного хорде x − 2 y − 2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Решение. Диаметр AB проходит через центр окружности C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
|
- 6x + 9)+ |
(y |
|
-14 y + 49)= 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Приведем уравнение окружности к каноническому виду 2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
или (x - 3)2 + (y + 7)2 = 82 , откуда C (3, 7). По условию задачи диаметр AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
перпендикулярен данной прямой x − 2 y − 2 = 0 , значит, по условию перпендикулярности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
двух прямых |
k1 × k2 |
= -1 , получим k AB = -2 , т.к. угловой коэффициент данной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
прямой k2 = |
1 |
. Итак, прямая AB : y - y0 = k AB (x - x0 ), или (y + 7) = -2(x - 3) , или 2x + y + 1 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
2x + y + 1 = 0 . |
|||||||||||||||
|
|
|
|
|
|
Задача 7. Написать каноническое уравнение эллипса, у которого расстояние от одного из фокусов до концов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
большой оси равно 5 и 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
Решение. |
Общий вид канонического уравнения эллипса |
3 : |
|
|
|
x2 |
|
+ |
y 2 |
= 1 , |
где a = 0 A1 = 0 A2 – большая полуось |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
эллипса, а b = 0B1 = |
0B2 - малая полуось эллипса. Найдем их. По |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
условию задачи A1 F1 = 1, A2 F1 = 5 , следовательно, A1 A2 = 6 или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 (0, |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
2a = 6 , |
a = 3 , |
F1F2 |
= 2c = 5 -1 = 4 – |
фокусное расстояние эллипса, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
откуда c = 2 – |
полуфокусное расстояние. Зависимость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
между параметрами |
|
|
a , |
b , c у эллипса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 (− 2, 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 (2, 0) |
|
|
x |
||||||||||||||||||
a 2 = b2 + c2 b2 = a 2 - c2 = 9 - 4 = 5 . Таким образом, каноническое |
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
F2 (1, 0) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
F1 (− 1, 0) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
уравнение эллипса: |
|
|
x2 |
+ |
y 2 |
|
= 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 (0, − |
3 ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
x2 |
|
+ |
y 2 |
= 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 8. Найти полуоси, координаты вершин, фокусов, эксцентриситет эллипса 3x2 + 4 y 2 -12 = 0 . Построить его.
21
|
Решение. |
|
|
|
|
|
|
|
|
x2 |
+ |
y 2 |
= 1 или |
x2 |
|
+ |
y 2 |
= 1 , откуда a = 2 ; b = |
|
|
|
|
||||||
|
Приведем уравнение эллипса к каноническому виду |
|
3 , |
|||||||||||||||||||||||||
|
a 2 |
b2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a2 = b2 + c2 , то c = |
|
|
= |
|
|
|
= 1 . Таким образом: |
A (− 2, 0); |
A (2, 0) ; |
B (0, |
|
); B |
|
(0, − |
|
); |
||||||||||
|
|
a2 − b2 |
|
|||||||||||||||||||||||||
т.к. |
для эллипса |
|
4 − 3 |
3 |
2 |
3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
|
|
|
|
|
|
|
||
F (−1, 0) ; F (1, 0) . Эксцентриситет эллипса ε = |
c |
|
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
2 |
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 9. |
Привести уравнение кривой к каноническому виду: 8x2 + 3 y 2 −16x |
||||
найти ее эксцентриситет. |
|
|
|
||
Решение. |
Выделим в уравнении кривой полные квадраты по |
||||
x и y : 8(x2 − 2x +1)+ 3(y 2 + 4 y + 4)= 8 + 12 + 4 или |
(x −1)2 |
+ |
(y + 2)2 |
= 1 . Из уравнения |
|
|
|
||||
|
3 |
8 |
|
||
x видно, что центр симметрии эллипса (данной кривой) находится в точке C (1, − 2) ;
a = |
|
- малая и b = |
|
– большая полуоси эллипса, c = |
|
= |
|
; ε = |
c |
= |
|
5 |
|
. |
|
|
|
b2 − a 2 |
|||||||||||||
3 |
8 |
5 |
|||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
b |
8 |
|
|
|||
Ответ: ε = 1 . 2
+12 y − 4 = 0 . Построить эту кривую,
y
|
|
B1 |
|
|
F1 |
|
x |
|
|
0 |
|
A |
C( 2 , −2 ) A |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
|
Ответ: ε = |
|
|
5 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
|||
|
|
|
|
|
|
|
|
|
8 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 10. Дана гипербола |
x2 |
− |
y 2 |
= 1 . Найти координаты ее вершин, |
фокусов, |
эксцентриситет и уравнения |
||||||||||
|
|
|||||||||||||||
9 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
асимптот этой гиперболы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Каноническое уравнение гиперболы |
x2 |
− |
y 2 |
= 1 4 |
, следовательно, для данной гиперболы a = 3 , b = 1 . |
|||||||||||
a 2 |
b2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Зависимость между параметрами гиперболы: c2 = a 2 + b2 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||
c = 
 a 2 + b2 , c =
a 2 + b2 , c = 
 9 +1 =
9 +1 = 
 10 . Значит, A1 (− 3, 0) ; A2 (3, 0);
10 . Значит, A1 (− 3, 0) ; A2 (3, 0);
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 (0,1) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B (0, 1); B |
|
(0, −1); |
F (− 10, 0); |
F ( 10, 0); ε = |
c |
|
= |
|
|
10 |
; асимптоты: |
A (− 3, 0) |
|
A (3, 0) |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
a |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ± |
b |
x или y = ± |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 (− 10 , 0) |
|
0 |
|
|
F2 ( 10 , 0) |
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x . (Ответ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 (0, − 1) |
|
|
|
|
|
|
|||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Задача 11. Привести уравнение кривой к каноническому виду и построить ее: |
x2 − 2 y 2 + 2x + 12 y − 33 = 0 . |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
Решение. |
|
Приведем |
уравнение к |
|
каноническому виду, |
выделив |
полные |
квадраты |
по |
|
x и |
y : |
|||||||||||||||||||||||||||||||
(x2 + 2x + 1)− 2(y 2 − 6 y + 9)= 33 + 1−18 или |
(x + 1)2 |
|
− |
(y − 3)2 |
|
4 , из уравнения |
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
следует, что центр симметрии кривой C(−1, 3), a = 4 |
|
- действительная, |
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b = |
8 - мнимая полуоси гиперболы; |
c = a 2 + b2 |
= |
16 + 8 = 2 6 - |
|
|
|
B |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
F |
|
|
F2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
C2 |
|
|
|
|
|
|
|||
полуфокусное расстояние гиперболы |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
0 |
|
|
|
|
||||
Задача 12. Привести уравнение кривой y = 3x2 −12x + 9 к каноническому виду, построить кривую |
. |
|
y |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. Преобразуем данное уравнение. Выделив по x полный квадрат: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
y = 3(x2 − 4x + 4)−12 + 9 или (x − 2)2 = |
1 |
(y + 3) - это каноническое уравнение параболы |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(x − a)2 = 2 p(y − b) |
5 . Из этого уравнения видно, что вершина параболы - |
C(2, − 3), ось |
|
|
|
0 |
C (2, |
− 3 ) |
x |
||||||||||||||||||||||||||||||||||||
симметрии параллельна оси 0 y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
22

Задача 13. Камень, брошенный под острым углом к горизонту, описал дугу параболы и упал на расстоянии 16 м от начального положения. Определить параметр параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12 м. y
Решение. Выберем систему таким образом, чтобы можно было задать параболу
каноническим |
5 |
|
уравнением вида x2 = -2 py . Из условий задачи видно, что в этой |
|
|
|
|||
системе координат координаты точек A(- 8, -12) , B(8, -12) , т.к. AB = 16 , OK = 12 . |
|
0 |
|
||||||
Подставим координаты одной из них в уравнение параболы: (- 8)2 = -2 p(-12) , |
|
|
|
||||||
отсюда p = |
64 |
= |
8 |
= 2 |
2 |
. |
A |
K |
B |
|
|
|
|||||||
24 |
3 |
3 |
|
|
|
|
|||
Ответ:
Задача 14. Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которого равен
x
p = 2 2 . 3
p = 0,1 .
Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 м от места выхода.
Решение. Решая эту задачу, можно воспользоваться рисунком предыдущей задачи и уравнением параболы x2 = -2 py . По условию задачи известно, что p = 0,1 м, AB = 2 , следовательно, A(-1, y), B(1, y),. Подставим в уравнение параболы данный параметр и координаты точки, через которую проходит парабола, например A(-1, y): (-1)2 = -2 × 0,1× y ,
откуда y = −5 . Это ордината точек A и B , а также и высота параболы h , следовательно, h = OK = 5 .
Ответ: h = 5
3.3 Кривые в полярной системе координат
Полярная система координат задается на плоскости точкой O – полюсом и лучом Oρ – полярной осью.
|
M (ρ , ϕ ) |
|
Положение точки |
M относительно полярной системы координат определяют ее |
|||||||||||||
|
|
|
|||||||||||||||
|
|
полярные координаты: |
ρ |
- полярный радиус, равный расстоянию точки M от полюса O , |
|||||||||||||
ρ |
|
т.е. ρ = OM , и ϕ - полярный |
угол, |
который образует |
полярный радиус с полярной осью. |
||||||||||||
ϕ |
|
Пишут: M (ρ, ϕ ) , где −∞ < ρ < ∞ , 0 ≤ ϕ < 2π . |
|
|
|
||||||||||||
0 |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связь между декартовыми и полярными координатами точки M . Если |
полюс полярной системы координат |
||||||||||||||||
совместить с началом координат декартовой системы, |
а полярную ось направить по оси 0x , то между декартовыми и |
||||||||||||||||
полярными координатами одной и той же точки M (x, |
y) M (ρ, ϕ ) |
|
легко обнаружить следующую зависимость, которую |
||||||||||||||
иллюстрирует рисунок: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
M |
|
x = |
ρ cosϕ |
|
|
ρ |
2 |
= x |
2 |
+ y |
2 |
|
|
|
||
|
|
|
Û |
|
|
|
|
|
|
|
|||||||
ρ |
|
|
|
ρ sin ϕ |
ϕ = arctg |
y |
|
|
|
||||||||
|
y |
|
y = |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ |
|
x, ρ |
Замечание: Чтобы правильно выбрать угол, имеющий тангенс, равный |
y |
, следует |
||||||||||||
|
|
||||||||||||||||
0 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
иметь в виду положение точки относительно декартовой системы координат. |
||||||||||||||||
|
|
|
|||||||||||||||
Приведем примеры некоторых кривых на плоскости, заданных в полярной системе координат.
y |
|
1. Окружность |
y |
y |
|
|
|
2R |
|
|
|
|
|
M (ρ , ϕ ) |
|
|
M (ρ , ϕ ) |
|
||||
|
|
M (ρ , ϕ ) |
|
|
|
R |
M (ρ , ϕ ) |
|
|||||
|
|
|
|
ρ |
|
|
|
ρ |
|
||||
|
ϕ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
ϕ |
|
|
|
|
|
||||
|
x, ρ |
|
|
|
x, ρ |
|
|
ϕ |
x, ρ |
||||
0 |
0 |
0 |
0 |
|
|
|
|
0 |
0 |
|
|||
|
|
|
|
||||||||||
|
R |
|
2R |
|
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 + y 2 = R 2 |
|
(x - R)2 + y 2 = R 2 |
|
|
x2 + (y - R)2 = R 2 |
|
|||||||
|
|
|
|
||||||||||
или ρ = R . |
|
или ρ = 2R cos ϕ . |
|
|
или ρ = 2R sin ϕ . |
|
|||||||
23

2. Спираль Архимеда ρ = aϕ .
0 |
2πa |
ρ |
|
|
2a |
0 |
ρ |
|
а) ρ = a(1− cosϕ ) ;
ρ
0
в) ρ = a(1 − sin ϕ ) ;
0 |
a |
ρ ρ = a cos 3ϕ |
 a
a
ρ ρ = a sin 3ϕ
0
трехлепестковые
3. Лемниската Бернулли ρ 2 = a2 cos 2ϕ .
|
|
π |
|
|
4 |
0 |
|
ρ |
|
|
π |
4. Кардиоида |
|
− |
|
4 |
|
0 |
2a |
ρ |
|
б) ρ = a(1+ cosϕ );
2a
0 |
ρ |
|
г) ρ = a(1 + sin ϕ ) .
5. Розы
ρ ρ = a cos 2ϕ
a
a
ρ ρ = a sin 2ϕ
четырехлепестковые
3.4 Параметрический способ задания кривых на плоскости
Некоторые кривые на плоскости удобно задавать уравнениями вида |
x = x(t ) |
, |
где зависимость между функцией y |
||
|
|||||
|
|
|
y = y(t ) |
|
|
и аргументом x устанавливается через посредство параметра (промежуточной переменной) t , причем − ∞ < t < ∞ . |
|||||
1. Параметрические уравнения прямой l: |
|
|
|
||
x = x0 |
+ mt |
R |
|
t |
- параметр. |
|
, где M 0 (x0 , y0 ) l ; s = {m; n} - направляющий вектор прямой l , |
||||
y = y0 |
+ nt |
|
|
|
|
2. Окружность: x = R cos t ; y = R sin t . |
|
|
|
||
3. Эллипс: x = a cos x ; |
y = b sin t . |
|
|
|
|
3. Циклоида: - это линия, которую описывает неподвижная точка на окружности, в то время, как окружность без
скольжения катится по оси 0x . y
|
C |
2a |
M |
t a |
|
|
2πa |
|
0 |
|
x = a(t − sin t )= ( − )y a 1 cos t
x
24
4. Астроида:
y
x = a cos3 ty = a sin 3 t
0 |
x |
3.5 Плоскость в пространстве
1 F (x, y, z) = 0 -поверхность.
2 |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|||
|
|
(α ) |
: |
Ax + By + Cz + D = 0 |
- плоскость, где |
N = {A, B, C} (α ) |
- нормаль |
R(α ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(α ) |
|
|
|
|
|
|
|
|
|
|
R |
{0, B, C} |
|
|
||
|
: |
Ax + By + Cz + D = 0 |
|
|
|||||||||||||
|
|
|
|
|
|
N |
|
|
|||||||||
|
D = 0 (0, 0, 0) (α ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(α ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Плоскость |
проходит |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Через начало координат |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
||||||||
|
|
0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x
7 |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|||||
(α ) |
By + Cz + D = 0 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
N {0, B, C} |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
A = 0 N = (0, B,C ) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(α ) |
|| |
|
OX |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плоскость |
(α ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
параллельна |
|
|
|
|
0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
оси |
OX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
By + Cz + D = 0 |
|||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Ax + By = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
C |
= D = 0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
R |
{A, B,O} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
N = |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(0,0,0) (α ) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
N {A, B, 0} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
(α ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
OZ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Плоскость проходит |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ax |
+ By = 0 |
|
|
|
|||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
через ось |
OZ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
Уравнение |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
C 1 {0 , 0 , c} |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
плоскости в отрезках |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
на осях: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N {A, B , C} |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||||||
x |
+ |
|
|
y |
+ |
z |
= 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 {0, b , 0 |
} |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||||||||||
a |
|
|
|
b |
|
|
c |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 {a , 0, 0} |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
Уравнение плоскости, проходящей |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
через точку |
M (x0 , |
y0 , z0 ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
перпендикулярно данному вектору |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
{A, B,C}: |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N = |
|
|
|
||||||||||||||||||||||||||
A(x − x0 )+ B(y − y0 )+ C(z − z0 ) = 0 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координатные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
y = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
z = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
Расстояние от точки |
|
M (x |
0 |
, |
|
y |
0 |
, z |
0 |
) |
|
|
|
|||||||||||||||||||
|
до плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(α ) |
|
|||||||||||||||||||||||||||||||||
|
|
Ax + By + Cz + D = 0 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d = |
|
Ax0 + By0 + Cz0 + D |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A2 + B 2 + C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
10 |
|
|
Уравнение |
плоскости, |
|
|
|
|
проходящей |
||||||||||||||||||||||||||
|
|
|
три данные |
|
точки: |
|
M1 (x1 , y1 , z1 ); |
||||||||||||||||||||||||||||
через |
|
|
|
||||||||||||||||||||||||||||||||
M 2 (x2 , y2 , z2 ) и M 3 (x3 , y3 , z3 ):
|
x − x1 |
y − y1 |
z − z1 |
|
|
|
|
|
|
||||
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|
|
. |
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
(α )1 |
|
A1 x + B1 y + C1 z + D1 = 0 |
(α )2 |
A2 x + B2 y + C2 z + D2 = 0 |
. |
||||||||||||||||||||||||||||
|
|
|
|
Угол между двумя плоскостями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
A A + B B + C C |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
R R |
|
|
|
|
|
N N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
cosϕ = cos(α1 α 2 )= cos(N1 N |
2 )= |
|
1 |
2 |
|
|
|
= |
|
|
|
|
1 |
2 |
1 |
2 |
1 2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
N 2 |
|
|
|
|
A 2 |
+ B 2 |
+ C |
2 |
|
A |
2 + B |
2 |
+ C |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
2 |
|
2 |
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
|
|
|
+ C1C2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(α1 ) (α 2 ) N1 |
N 2 A1 A2 + B1 B2 |
-условие перпендикулярности двух плоскостей, |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
R |
|
|
|
R |
|
|
B1 |
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(α1 ) |
|| |
(α |
2 ) |
N1 |
|| |
|
N2 |
A1 |
|
+ |
+ |
|
- условие параллельности двух плоскостей. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25

Задачи по теме «Плоскость в пространстве»
Задача1. Составить уравнение плоскости (α ) , параллельной плоскости XOZ и проходящей через точку M (2, - 5, 3).
Решение. |
Искомая плоскость |
(α ) |
параллельна координатной плоскости XOZ , значит, |
параллельна осям OX и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
OZ . Следовательно, в общем уравнении (α ) A = 0 , C = 0 |
7 , т.е. оно имеет вид By + D = 0 , где B ¹ 0 , |
D ¹ 0 . Найдем B и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D . Так как точка M Î (α ), то ее координаты должны удовлетворять уравнение (α ) : B(- 5)+ D = 0 D = 5B , подставив D в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнение (α ) |
и сократив на B , получим By + 5B = 0 или y + 5 = 0 (α ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (α ) |
y + 5 = 0 . |
||||||
Задача 2. Составить уравнение плоскости (α ) , проходящей через ось OZ и через точку M (- 3, 1, - 2). |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
Плоскость (α ) , проходящая через ось OZ , проходит через начало координат параллельно оси OZ , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
значит, в общем уравнении (α ) D = 0 , |
|
C = 0 , т.е. оно имеет вид |
Ax + By = 0 , |
где A ¹ 0 , B ¹ 0 |
|
3 и |
7 . Так как точка |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
M Î (α ), то ее координаты должны удовлетворять уравнение (α ) : |
A(- 3)+ B ×1 = 0 B = 3A . Подставим B в уравнение (α ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и сократим на A : Ax + 3Ay = 0 , получим x + 3y = 0 - уравнение (α ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (α ) x + 3y = 0 . |
|||||||||
Задача 3. Найти объем пирамиды, отсекаемой плоскостью 2x - 3y + z -12 = 0 от координатного угла. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
Приведем уравнение данной плоскости к виду «уравнение в отрезках |
|
|
|
|
|
|
|
z |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
на осях» 5 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C (0, 0,12) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
z |
= 1 . Откуда a = 6 , b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
+ |
|
|
|
+ |
|
= 1 2x - 3y + z -12 = |
0 или |
|
+ |
|
|
+ |
|
|
= -4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
- 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
a |
|
|
|
b |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
c = 12 – отрезки, отсекаемые плоскостью от осей координат, совпадающие с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
ребрами пирамиды OABC . Так как они взаимно перпендикулярны, то |
B(0, − 4,0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
1 |
|
a ×b × c |
|
= |
1 |
6 × 4 ×12 = 48 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(6, 0,0) |
|
|
|
|
0 |
|
|
|
|
y |
|||||||||||||||
Vпир |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
Ответ: Vпир = 48 куб.ед. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Задача 4. |
Составить уравнение плоскости |
|
|
(α ), проходящей через точку |
M (- 2, 7,3) |
параллельно плоскости |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
x − 4 y + 5z −1 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если две плоскости параллельны, |
то их нормали тоже параллельны 11 , N |
1 |
|| N |
2 |
. Поэтому в качестве |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
{1, - 4, 5}. Уравнение плоскости, проходящей |
|||||||||||||||||||
нормали к искомой плоскости можно взять нормаль к данной плоскости |
N1 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
через данную точку M (x0 , y0 , z0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= {A, B,C}: |
A(x - x0 )+ B(y - y0 )+ C(z - z0 ) = 0 6 , |
||||||||||||||||||||||||||||||||||||
перпендикулярно данному вектору |
N1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
следовательно, искомая плоскость: 1(x + 2)- 4(y - 7)+ 5(z - 3) = 0 или x − 4 y + 5z + 15 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (α ) |
x − 4 y + 5z + 15 = 0 . |
|||||||||||||
Задача 5. |
Даны две точки: |
P(1, 3, - 2) и |
Q(7, - 4, 4) . Через точку |
Q провести плоскость, |
перпендикулярную |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
отрезку PQ . Найти направляющие косинусы нормали к плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решение. |
Воспользуемся |
уравнением |
плоскости, проходящей |
через |
данную точку перпендикулярно |
данному |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
вектору A(x - x0 )+ B(y - y0 )+ C(z - z0 ) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
{A, B,C}: вектор PQ = {6, - 7, 6}. Тогда уравнение |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
6 . Примем за нормаль N1 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плоскости: |
|
|
6(x - 7)- 7(y + 4)+ 6(z - 4) = 0 |
|
|
или |
|
6x − 7 y + 6z − 94 = 0 . |
Чтобы |
найти |
направляющие |
косинусы |
вектора |
|||||||||||||||||||||||||||||||||||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
62 + (- 7)2 + 62 = 11 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
N = {6, - 7, 6}, найдем его орт: N 0 |
= |
|
; |
|
N |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
7 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||||||
Следовательно: N 0 = |
6 |
, - |
, |
|
|
= {cosα , cos β , cosγ } или cosα = |
; cos β = - |
; cosγ = |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
11 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
|
|
|
11 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
6x − 7 y + 6z − 94 = 0 ; cosα = |
6 |
; cos β = - |
7 |
; cosγ = |
6 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
11 |
11 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Задача 6. |
Найти объем куба, если |
грани |
его лежат на |
плоскостях |
(α1 ) |
11x − 2 y −10z +15 = 0 |
и (α 2 ) |
11x − 2 y −10z − 45 = 0 . |
|
|
|
|
|
|
|
Решение. |
Объем куба V = a3 , где a – |
длина |
ребер куба. |
Ребро куба |
равно |
расстоянию между |
данными |
плоскостями, т. к. эти плоскости параллельны (коэффициенты при переменных пропорциональны), значит, на этих плоскостях лежат противоположные грани куба. Чтобы найти расстояние между двумя плоскостями, воспользуемся
формулой |
|
d = |
|
|
Ax0 + By0 + Cz0 + D |
|
|
9 . Для этого на одной из плоскостей выберем произвольную точку, например |
|||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
A2 + B2 + C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
- 45 |
|
|
|
60 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
11× 0 - 2 × 0 -10 × |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Îα1 , и найдем расстояние от нее до второй плоскостиα |
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
M |
0, 0, |
|
|
|
2 : d = |
|
|
|
|
|
|
|
|
= |
|
= 4 . |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
112 + (- 2)2 + (-10)2 |
|
|
|
|
15 |
|
||||
|
Итак, a = d = 4 Vкуб |
= a3 |
|
= 43 = 64 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Vкуб |
= 64 . |
|
|
Задача |
7. |
|
|
Найти |
точку пересечения |
данных плоскостей: |
|
5x + 8y − z − 7 = 0 |
|
(α1 ), |
|
x + 2 y + 3z −1 = 0 |
(α 2 ), |
||||||||||||||||||||||||||||||||||||||||||
2x − 3y + 2z − 9 = 0 (α 3 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение. |
Чтобы найти точку пересечения трех плоскостей, т. е. общую точку этих трех плоскостей, достаточно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 y + 3z = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
решить систему их уравнений: |
|
|
|
|
|
|
= 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5x + 8y - z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3y + 2z = 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Используем метод Гаусса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
-5 |
1 2 |
|
3 |
|
1 |
|
1 |
2 |
|
3 |
|
1 |
|
1 2 |
3 |
|
|
|
1 |
|
|
1 |
2 |
3 |
|
1 |
|
x + 2 y + 3z = 1 x = 1 - 2 y - 3z = 3 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
-1 |
|
|
|
|
- 2 -16 |
|
|
|
|
|
-1 |
- 8 |
|
|
|
|
|
-7 |
|
-1 - 8 |
|
|
|
|
|
|
|
|
- y - 8z = 1 y = -1 |
|
|||||||||||||||||||||||
-2 5 8 |
|
7 ~ |
0 |
|
2 ~ 0 |
|
|
1 |
|
|
~ 0 |
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
- 3 |
|
2 |
|
9 |
|
|
- 7 - 4 |
|
|
|
|
|
- 7 |
- 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52z = 0 z = 0. |
|
|
|||||||||||||||
|
2 |
|
|
|
0 |
|
7 |
|
0 |
|
|
7 |
|
|
0 |
0 52 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: M (3, -1, 0) . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Задача 8. |
Найти угол между плоскостью x - y + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
z - 5 = 0 и плоскостью YOZ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
||
|
Решение. |
|
Угол между двумя плоскостями можно найти по формуле |
cosϕ = |
|
N1 N |
2 |
|
|
9 |
; нормаль к первой |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
R |
× |
|
R |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
N |
2 |
|
|
|
|
|
|
|||||
|
|
R |
{1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= {1, 0, 0}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
плоскости |
N1 = |
-1, |
|
2}; уравнение второй плоскости YOZ x = 0 N 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A1 A2 + B1B2 + C1C2 |
|
|
|
|
|
|
|
|
|
|
1×1+ (-1)×0 + |
|
×0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
||||||||||||||||
|
Вычислим cosϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
1 |
, т. е. ϕ = |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
3 . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 + (-1)2 + ( |
|
)2 |
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||
|
|
A1 |
2 + B1 |
2 + C1 |
2 × |
|
A2 |
2 + B2 |
2 + C2 |
2 |
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
12 + 02 + 02 × |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: ϕ = π . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
Задача 9. |
|
|
Найти длину высоты пирамиды |
SABC , |
опущенной из вершины S |
на грань |
|
ABC , если |
S(1, 4, - 2) , |
||||||||||||||||||||||||||||||||||||||||||||||
A(0, -1, 1), B(3, 5, 1) , C(1, - 3, -1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Решение. |
Длина высоты |
SO – это длина перпендикуляра, опущенного из вершины |
S |
пирамиды на плоскость ее |
|||||||||||||||||||||||||||||||||||||||||||||||||||
основания, с помощью которого измеряется расстояние от точки |
S до плоскости основания |
ABC . |
Составим уравнение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
плоскости ABC , проходящей через три данные точки A , |
B и C , для этого воспользуемся уравнением 10 : |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
x - x1 x2 - x1 x3 - x1
y - y1 y2 - y1 y3 - y1
z - z1 |
|
|
|
x - 0 y +1 z -1 |
|
|
|
x y +1 z -1 |
|
= 0 ; |
||
|
|
|
|
|
||||||||
z2 - z1 |
|
= 0 ; |
|
3 - 0 5 +1 1-1 |
|
= 0 ; |
|
3 |
6 |
0 |
|
|
z3 - z1 |
|
|
|
1- 0 - 3 +1 -1-1 |
|
|
|
1 |
- 2 - 2 |
|
|
|
-12x + 6(y +1)-12(z -1) = 0 12x − 6 y + 12z −18 = 0 или 2x − y + 2z − 3 = 0 -
уравнение плоскости основания пирамиды. |
Расстояние d |
(высота SO ) можно |
найти по |
||||||||||||||||
формуле расстояния от точки до плоскости |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SO = d = |
|
|
Ax0 + By0 + Cz0 + D |
|
|
= |
|
|
2 ×1 |
-1× 4 + 2 ×(- 2)- 3 |
|
|
= |
9 |
= 3 . |
||||
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A2 + B2 + C 2 |
22 + (-1)2 + 22 |
|
|
|
|
3 |
|
||||||||
Ответ: SO = 3 .
27
|
Задача 10. |
Найти уравнение плоскости |
(α ) , |
проходящей |
через точку |
M 0 (2, − 3, 1) |
параллельно |
векторам |
||||||||
R |
= {− 3, 2, −1} и b = {1, 2, 3}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. |
Уравнение плоскости, |
проходящей |
через |
|
данную |
точку |
перпендикулярно |
данному |
вектору |
||||||
A(x − x0 )+ B(y − y0 )+ C(z − z0 ) = 0 : 11 , |
точка |
M 0 (x0 , y0 , z0 ) задана в |
условии задачи; в качестве |
нормального |
вектора |
|||||||||||
N1 = {A, B,C}можно |
взять векторное |
произведение |
векторов |
R |
и |
b , |
которые |
параллельны |
плоскости |
(α ) , т. к. |
||||||
a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× b |
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
N = a |
|
|
||
c |
= a × b будет перпендикулярен искомой плоскости (α ) . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
R |
R |
R |
|
|
|
|
R |
|
|
R |
|
i |
j |
k |
R |
R |
R |
= {8, 8, − 8} 9 |
R |
R |
= |
− 3 |
2 |
−1 |
||||||
N = c |
= a |
× b |
= 8i |
+ 8 j |
− 8k |
||||||
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (α ): 8(x − 2)+ 8(y + 3)− 8(z −1) = 0 , сократив на 8, получим
(x − 2)+ (y + 3)− (z −1) .
Ответ: x + y − z + 2 = 0 .
|
R |
|
b |
R |
|
a |
|
M 0 (2, − 3,1) |
α |
|
3.6 Прямая в пространстве
|
|
|
|
|
|
|
1 |
|
|
F (x, y, z) = 0 − поверхность |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
F1 (x, y, z) = 0 − поверхность |
|
- линия пересечения |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 x + B1 y + C1 z |
+ D1 |
= 0 − плоскость |
|
|
|
|
|
|
|
|
R |
|
||||||||||
|
|
|
|
|
l |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
- прямая |
|
R |
|
|
S |
|
||||||||
|
|
|
|
|
A2 x + B2 y + C2 z |
+ D2 |
|
= 0 − плоскость |
|
|
|
|
|
N |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Это общие уравнения прямой |
l |
; |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
R |
= (A1 , B1 , C1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
- нормаль к пл. α1 , |
|
|
|
|
|
|||||||||||||||||
|
N1 |
α |
|
R |
||||||||||||||||||||
2. |
|
R |
= (A2 , B2 ,C2 ) |
- нормаль к пл. α 2 , |
1 |
|
N2 |
|||||||||||||||||
|
N1 |
|
|
|
|
|
||||||||||||||||||
|
A1 |
x + B1 y + C1 z + z1 |
+ λ(A2 x + B2 y + C2 z + D2 ) = 0 |
- |
|
|
|
α2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|||||
|
уравнение пучка плоскостей, проходящих через прямую |
. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
Каноническое уравнение прямой l : |
|
|
: |
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
|
, где |
|
|
|
|
, |
|
||||
l |
M |
0 (x0 , y0 , z0 ) l |
|
||||||||||||||||
|
m |
|
n |
p |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
R |
|
|
|
|
|
|
|
|
|
R |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= {m, n, p} |
- направляющий вектор прямой |
l |
|| l . |
||||||||||||||||
s |
: s |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
l |
S
M (x, y, z )
M 0 (x0 , y0 , z0 )
4 Уравнение прямой l , проходящей через
две данные точки M1 (x1 , y1 , z1 ) и M 2 (x2 , y2 , z2 ) . Направляющий вектор прямой
R |
= M1M 2 |
= {x2 − x1 , y2 − y1 , z2 − z1}= {m, n, p}. |
S |
Через любую из данных точек проводим прямую:
x − x1 = y − y1 = z − z1 x2 − x1 y2 − y1 z2 − z1
l
M 2 (x2 , y2 , z2 )
R
S
M 1 (x1 , y1 , z1 )
5 |
Общие уравнения прямой |
|
|
|
: |
(α1 ) |
A1 x + B1 y + C1 z + D1 = 0 |
привести к каноническому виду: |
||||||||||||||||||||||
|
l |
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(α |
2 |
) A x + B y + C |
2 |
z + D = 0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x − x0 |
= |
y − y0 |
= |
z − z0 |
|
|
выберем любую точку |
|
|
, подобрав x0 , |
|
|||||||||||||||||||
|
. На прямой |
l |
|
|
M 0 (x0 , y0 , z0 ) |
y0 , z0 , |
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
m |
n |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
R |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
удовлетворяющие систему |
уравнений |
|
l |
Направляющим вектором S может |
служить |
|||||||||||||||||||||||||
|
|
R |
R |
R |
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вектор S |
= N1 × N 2 , т.к. |
N 2 и |
N1 |
перпендикулярны прямой |
l |
2 . |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|||

6Иногда удобно пользоваться параметрическими уравнениями прямой:
x= x0 + mt
|
|
|
|
|
x - x0 |
|
= |
|
y - y0 |
= |
|
|
z - z0 |
|
= t |
|
или |
|
y = y0 + nt ; где t |
- параметр, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = z0 + pt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
Угол между двумя прямыми |
|
|
|
|
и |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
l1 |
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
: |
|
x - x1 |
= |
y - y1 |
= |
z - z1 |
|
; |
|
|
|
|
|
|
|
|
|
x - x2 |
|
|
|
|
= |
|
y - y2 |
|
= |
z - z2 |
|
|
|
|
- это угол между их направляющими |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
l1 |
|
l2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= {m2 |
, n2 , p2 } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
векторами |
|
s1 = {m1 , n1 , p1} |
и |
|
s2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
× |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
m1m2 + n1n2 + p1 p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
|
|
S1 |
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
cosϕ = cos(l1 l2 )= cos(S1 S2 )= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
S2 |
|
|
|
|
|
|
|
|
m12 + n12 + p12 |
|
|
|
m2 2 + n2 2 + p2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
|
m1 |
|
n1 |
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Условие параллельности двух прямых: |
l1 || l2 |
S1 || S2 |
|
|
|
= |
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Условие перпендикулярности двух прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 ^ l2 S1 |
^ S 2 |
|
|
S1 × S 2 = 0 m1m 2 +n1n 2 + p1 p 2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
Дано : |
(α ) |
: |
Ax + By + Cz + D = 0 |
- плоскость, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x - x0 |
|
|
|
|
|
y - y0 |
|
|
|
|
|
z - z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|||||||||||||||||||
|
l |
: |
|
|
|
|
m |
|
= |
|
|
n |
= |
|
p |
|
|
|
- прямая. Угол между прямой |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
−ϕ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ϕ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и плоскостью |
(α ) |
|
- это угол |
|
|
|
|
между прямой |
l |
и |
|
l′ |
ее проекцией |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
l′ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= {A, B, C} |
|
|
|
|
= {m, n, p} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
на плоскость. Векторы |
N |
|
и |
S |
образуют угол |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Am + Bn + Cp |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
N × S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
-ϕ |
, |
значит, |
sin ϕ = cos |
|
|
-ϕ |
|
= cos(N |
S )= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
R |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
S |
|
|
|
|
A2 + B 2 + C 2 |
|
m 2 + n 2 + p 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
Условие параллельности прямой и плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 // α N ^ S N × S = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Am + Bn + Cp = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
Условие перпендикулярности прямой и плоскости: |
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 ^ α N || S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
A = B = C . m n p
α
l
Задачи по теме «Прямая и плоскость в пространстве»
|
|
|
|
Задача 1. Составить уравнение прямой l , проходящей через точку |
|
|
|
|
||||||||||
|
|
|
|
M 0 (1, - 2, 2) параллельно оси 0 y . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Решение. В канонических уравнениях |
прямой |
|
x - x0 |
= |
y - y0 |
= |
z - z0 |
3 точка M 0 (x0 , |
y0 , z0 )Îl , а вектор |
|||||
|
|
|
|
|
|
p |
||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
n |
|
|
|
||||
|
R |
= {m, n, p}– |
направляющий вектор прямой. |
|
|
|
|
|
|
|
|
|
|
0 y , следовательно, |
||||
|
S |
По условию задачи |
прямая |
параллельна оси |
||||||||||||||
направляющим вектором прямой может служить орт оси |
0 y вектор |
R |
= {0,1,0}. Итак, канонические уравнения прямой l |
|||||||||||||||
j |
||||||||||||||||||
|
x -1 |
= |
y + 2 |
= |
z - 2 |
. Приравнивая попарно отношения, получим общие уравнения ее (l ) x = 1 . |
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
z = 2 |
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 2 |
|||||
|
|
Задача |
2. |
|
|
Даны |
координаты вершин треугольника |
A(2, 3, -1) ; |
B(1, - 2, 0) ; |
|
C(- 3, 2, 2) . |
Составить уравнения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
медианы AM и найти ее длину. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
а) Найдем координаты точки M – |
середины отрезка BC по формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
xM = |
xB + xC |
= |
|
1- 3 |
|
= -1 ; yM = |
yB + yC |
= |
- 2 + 2 |
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
zM = |
zB + zC |
= |
2 + 0 |
= 1 , т.е. M (-1, 0, 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Через точки A и M проведем прямую AM , используя уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x - x1 |
= |
|
|
y - y1 |
= |
z - z1 |
|
или |
|
x - 2 |
= |
y - 3 |
= |
z +1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
x2 - x1 |
|
|
y2 - y1 |
z2 - z1 |
|
- 3 |
|
|
|
|
- 3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
б) Длину медианы AM можно найти по формуле расстояния между двумя точками: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
(x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 |
(2 +1)2 + (3 - 0)2 + (-1 -1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
AM = |
= |
|
= |
22 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 1) AM : |
|
x - 2 |
= |
|
y - 3 |
= |
|
z +1 |
: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 3 |
|
- 3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) AM = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Задача 3. Через точку M 0 (1, - 3, 5) провести прямую l , параллельную прямой l1 |
|
3x - y + 2z - 7 = 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
: |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 3y - 2z + 3 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллельны, то за направляющий вектор искомой прямой |
R |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Так как прямые l |
и |
l1 |
|
|
S можно принять |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющий вектор данной прямой |
|
S1 , |
который можно найти как векторное произведение нормалей к плоскостям, при |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
{3, -1, 2} |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
пересечении которых образуется данная прямая l : |
N1 |
= |
|
и N2 = {1, 3, - 2}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
R |
|
R |
i |
j |
|
|
|
k |
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Итак, S |
= S1 |
|
= N1 ´ N2 = |
3 |
-1 |
|
|
2 |
|
|
= -4i + 8 j |
+ |
10k 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Канонические уравнения прямой l : |
|
x -1 |
= |
|
y + 3 |
= |
z - 5 |
или |
x -1 |
= |
y + 3 |
= |
z - 5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
- 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
10 |
|
- 2 |
|
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: l : |
x -1 |
= |
y + 3 |
= |
z - 5 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y -1 |
|
|
z |
|
|
|
|
3x + y - 5z +1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Задача 4. Доказать, что прямыеl1 |
: |
|
|
= |
= |
|
|
и l2 : |
|
|
|
|
|
|
|
|
: перпендикулярны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- 2 |
|
|
|
3 |
|
|
|
|
2x + 3y - 8z + 3 = |
0 |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
Решение. Если прямые перпендикулярны, |
то перпендикулярны их направляющие векторы S1 и S2 7 |
. Из условий |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
задачи ясно, что |
S1 = {1, - 2, 3}, а направляющий вектор второй прямой |
S2 |
|
можно найти как векторное произведение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
R |
- 8}. Таким образом, |
||||||||||||||||||
нормалей плоскостей, заданных в общих уравнениях прямой |
l2 , т. е. N1 = {3, 1, - 5} |
|
и N2 = {2, 3, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R |
R |
|
R |
|
i |
|
|
|
j |
|
|
k |
= {7, 14, 7} 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
S2 |
= N1 |
´ N 2 = |
3 |
|
|
|
1 |
- 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
3 |
- 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
R |
R |
|
Скалярное |
|
|
|
|
|
|
произведение |
|
|
|
|
|
|
|
|
взаимно |
|
|
|
перпендикулярных |
|
векторов |
|
|
|
равно |
|
|
|
|
нулю: |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ z1 z2 = 1×7 + (- 2)×14 + 3×7 = 0 . Что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
S1 |
× S2 = x1 x2 + y1 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Задача |
5. |
Найти |
|
|
угол |
между |
|
прямой, |
|
проходящей |
через точки |
|
A(2, 3, -1) и B(1, - 2, 0) |
и плоскостью |
α : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x − 3y + z + 5 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Решение. Угол между прямой и плоскостью можно найти по формуле |
|
sin ϕ = |
|
|
Am + Bn + Cp |
|
|
8 |
|
|
, где |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 + B 2 + C 2 |
|
m2 + n2 + p 2 |
|
|
|
||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= {m, n, p}– направляющий вектор прямой AB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
N |
= {A, B, C} – нормаль к плоскости, а S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
30
