Лабораторна робота №1
Знайомство з середовищем MatLab.
Дії з матрицями в середовищі MatLab
Практичне заняття проводиться після вивчення теми «Мета та задачі дисципліни».
Мета заняття:
Вироблення у студентів навичок роботи в середовищі MatLab;
Вивчення основних операцій та функцій, за допомогою яких проводяться обчислення в середовищі MatLab, з метою їх подальшого використання при розв’язанні математичних завдань за темами.
1.1. Робоче середовище MatLab
Запуск MatLab приводить до відкриття робочого середовища, зображеного на рис. 1.1.
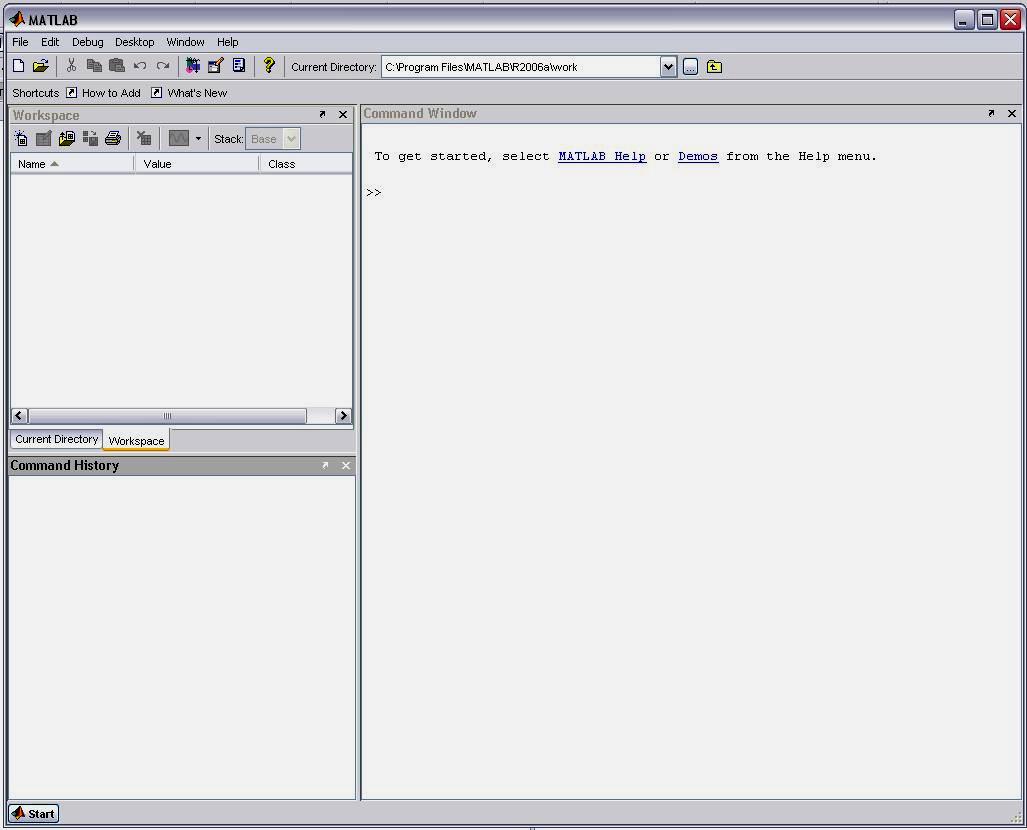
Рис.1.1. Вікно робочого середовища MatLab
Р
меню;
панель інструментів з кнопками й списками, що розкриваються;
вікно з вкладками Launch Pad (засіб для отримання швидкого доступу до різних модулів пакетів розширення (Toolboxes) MatLab), Command Window (усі розрахунки виконуються у ньому), Current Directory (використовується для встанови поточної директорії), Workspace (зберігаються змінні, що були отримані під час розрахунків), Command History (використовується для розгляду та повторного виклику раніш введених команд);
рядок стану
За бажанням користувача вид середовища може бути змінений за допомогою пункту меню Вид (View). Усі команди слід набирати в командному вікні, яке містить командний рядок. Командний рядок починається з символу «>>», що позначає запрошення до вводу команди.
При роботі з MatLab у командному режимі діє простий редактор. Його команди надані в таблиці 1.1.
Таблиця 1.1
Команди редактора MatLab
Комбінація клавіш |
«Гарячі» клавіші |
Призначення |
1 |
2 |
3 |
|
Ctrl+b |
Переміщення курсору праворуч на один символ |
|
Ctrl+f |
Переміщення курсору ліворуч на один символ |
Ctrl+ |
Ctrl+r |
Переміщення курсору праворуч на одне слово |
Ctrl+ |
Ctrl+l |
Переміщення курсору ліворуч на одне слово |
Home |
Ctrl+a |
Переміщення курсору на початок рядка |
End |
Ctrl+e |
Переміщення курсору в кінець рядка |
і |
Ctrl+p і Ctrl+n |
Перегортання попередніх команд вверх чи вниз для підстановки у рядок введення. |
Del |
Ctrl+d |
Стирання символу праворуч від курсору |
Backspace |
Ctrl+h |
Стирання символу ліворуч від курсору |
Ctrl+k |
Ctrl+k |
Стирання до кінця рядка |
Ecs |
|
Очищення рядка введення |
Ins |
|
Включення/виключення режиму вставки |
PageUp |
|
Перегортання сторінок вверх |
PageDown |
|
Перегортання сторінок вниз |
1.2. Розрахунки в MatLab
Обчислення математичних виразів у системі MatLab проводяться за допомогою арифметичних та матричних операцій (табл. 1.2), а також елементарних функцій (табл. 1.3).
Таблиця 1.2
Арифметичні та матричні операції в MatLab
Операція |
Призначення |
1 |
2 |
+, - |
Додавання та віднімання для чисел та матриць (матриці повинні мати однаковий розмір). Також один із доданків може бути числом, а другий матрицею (в цьому разі отримаємо матрицю того ж розміру, що й матриця-доданок, кожний елемент якої – це сума кожного елемента матриці-доданка і числа доданка) |
* |
Добуток чисел та матриць (матриці повинні мати розміри, що дозволяють їх перемножити). Також один із множників може бути числом, а другий матрицею (в цьому разі отримаємо матрицю того ж розміру, що й матриця-множник, кожний елемент якої – це добуток кожного елемента матриці-множника і числа-множника) |
/ |
Ділення
чисел, якщо обидва операнди – матриці,
то
|
^ |
Возведення в степінь для чисел і квадратних (!) матриць |
\ |
Ліве
матричне ділення. Якщо A
– це квадратна матриця, то
|
.* |
Поелементний
добуток матриць однакового розміру.
Якщо
|
./ |
Поелементне
ділення матриць однакового розміру.
Якщо
|
.\ |
Поелементне
ліве ділення матриць однакового
розміру. Якщо
|
.^ |
Поелементне
приведення матриці до степенів, що
являються елементами другої матриці.
Якщо
|
' |
Знаходження
спряженої матриці. Якщо
|
.' |
Транспонування.
Якщо
,
то
|
.
Якщо
– це квадратна матриця розміру
,
– вектор із
елементів,
то
– це розв’язок системи
за
методом Гауса. Якщо ж
– це прямокутна матриця розміру
,
– вектор із
елементів,
то
– це розв’язок системи
за
методом найменших квадратів.
,
то
,
то
,
то
,
то
,
то
.
Якщо елементами матриці є дійсні
числа, операції .'
і '
мають однаковий результат.
Таблиця 1.3