Дополнение 1. Корреляционное отношение и его свойства

Если линии регрессии не являются прямыми, то коэффициент корреляции лишь с некоторым приближением может рассматриваться как показатель связи между случайными величинами X и Y. В случае нелинейной связи представляют интерес показатели, характеризующие концентрацию распределения (и, следовательно, тесноту связи) около линий регрессии. Таким показателем является корреляционное отношение, введенное К. Пирсоном.

Разброс значений случайной величины Y около математического ожидания m_y=M[Y] измеряется дисперсией

.

Этот разброс может быть вызван двумя факторами: 1) влиянием корреляционной зависимости Y от X; 2) влиянием прочих (остаточных) факторов, не влияющих на X.

Влияние первого фактора измеряется величиной

, (4.37)

т.е. дисперсией линии регрессии относительно математического ожидания m_y.

Влияние второго фактора измеряется величиной

, (4.38)

т.е. дисперсией Y относительно линии регрессии.

В соответствие со свойствами дисперсии можно записать, что

. (4.39)

Корреляционным отношением Y на X называется отношение

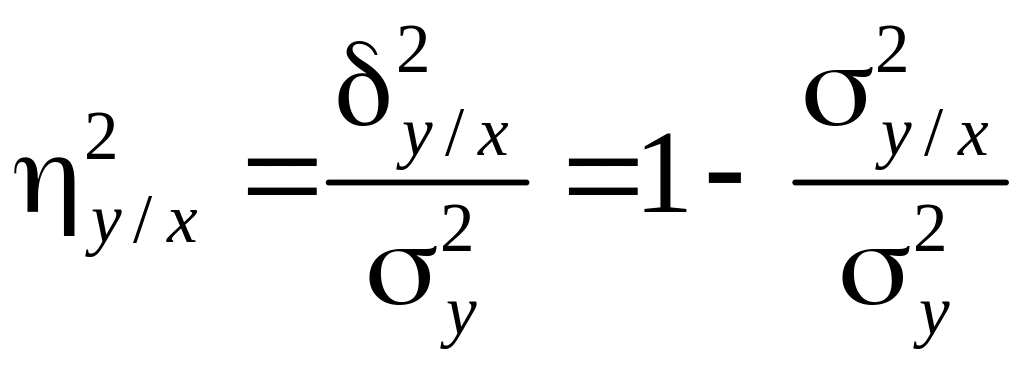. (4.40)

Аналогично определяется корреляционное отношение X на Y

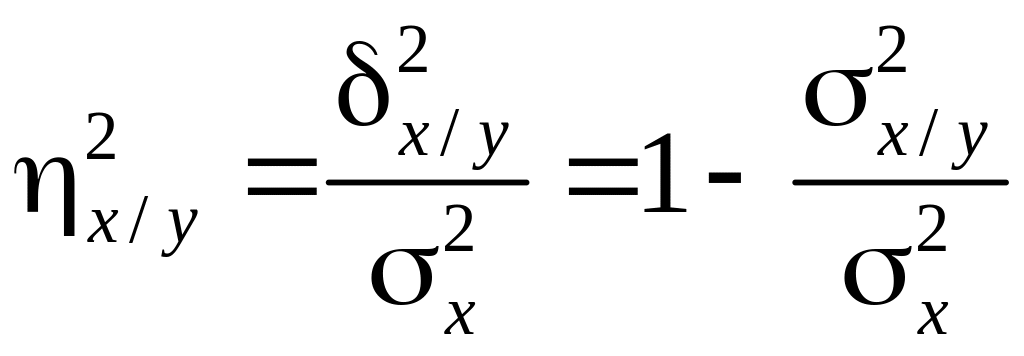. (4.41)

Рассмотрим теперь свойства корреляционного отношения.

1⁰. Корреляционное отношение всегда заключено между 0 и 1, т.е.

.

2⁰. Корреляционное отношение равно 0, тогда и только тогда, когда отсутствует корреляционная зависимость.

Действительно, пусть . Тогда Отсюда следует, что M[Y|x]=const, т.е. условное математическое ожидание "не реагирует" на изменения значений величины X (линия регрессии параллельна оси Oy). Это и означает, что корреляционная зависимость Y от X отсутствует. Справедливо и обратное утверждение, поскольку при отсутствии корреляционной зависимости M[Y|x]=const, поэтому D[M(Y|x)]=0 и _y/x=0.

3⁰. Корреляционное отношение равно 1, тогда и только тогда, когда существует функциональная зависимость (y=f(x) и x=g(y)).

Действительно, пусть . Тогда Но так как дисперсия неотрицательна, то D[Y|x]=0 при любом значении x, а 'это означает, что величина Y принимает единственное значение при котором x, т.е. зависимость Y от X функциональная. Справедливо и обратное утверждение. Из данного свойства следует, что чем ближе корреляционное отношение к единице, тем «концентрация» значений Y к линии регрессии.

4⁰. Коэффициент корреляции не превосходит по абсолютной величине корреляционное отношение:

|r|  

Отметим, что между _y/x и _x/y нет какой-либо простой зависимости. Например, Y может быть не коррелированно с X и _x/y=0, тогда как другой показатель может быть равен 1, т.е. _y/x=1.

Таким образом, поскольку коэффициент корреляции можно рассматривать как меру линейности регрессии, то величину

² – r²

можно рассматривать как меру нелинейности регрессии, т.е. отклонения линии регрессии от прямой.

5⁰. Выполнение равенства _y/x=|r_xy| является необходимым и достаточным условием того, чтобы регрессия Y на X была точно линейной. Аналогично и для _x/y.

Для того чтобы оценить корреляционное отношение исходные нужно сгруппировать в виде корреляционной таблицы. В каждой клетке этой таблицы приводятся численности n_ij тех пар (x,y), компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой из переменных) равными между собой, выбирают центры x_i (соответственно y_i) этих интервалов и числа n_ij в качестве основы для расчетов. Точечной оценкой корреляционных отношений являются выражения:

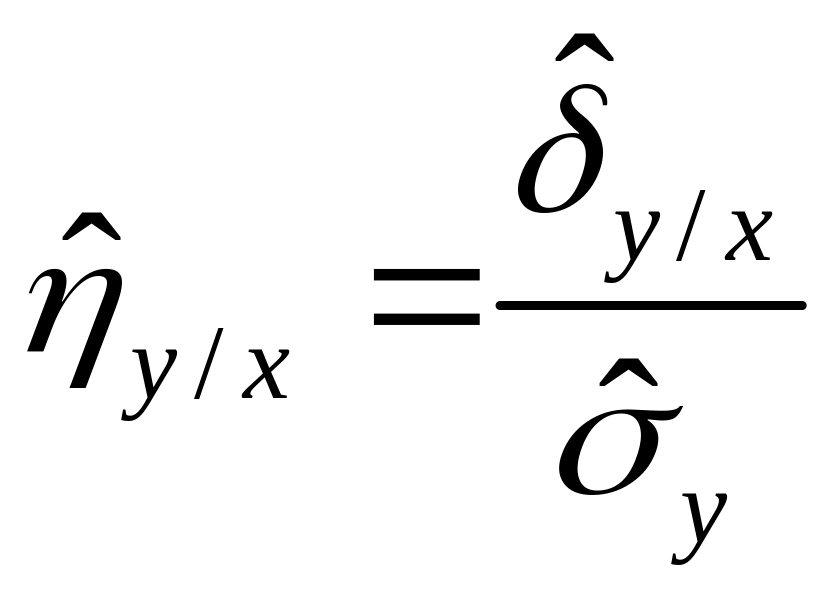и 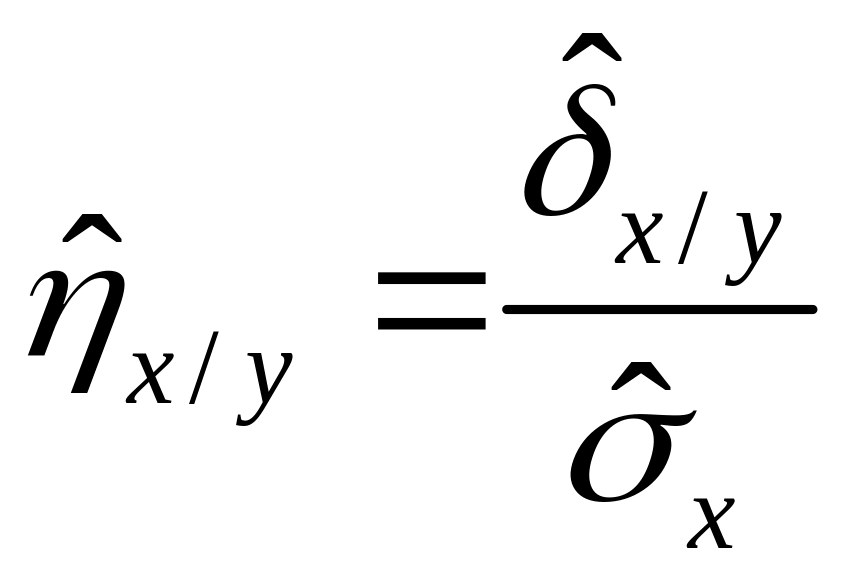(4.42)

где и – средние квадратичные отклонения условных средних от общей средней:

, . (4.43)

Отметим, что корреляционное отношение не меняется при переходе к новым переменным (4.26), т.е.

и .

Выше мы уже отмечали, что величину ² – r² можно рассматривать как меру нелинейности регрессии, т.е. отклонения линии регрессии от прямой. Поэтому величины

и (4.44)

можно рассматривать как меру нелинейности корреляционной зависимости. Если величины (4.44) значимо отличаются от нуля, то имеется нелинейная корреляционная зависимость, если не значимо, то имеющиеся данные не противоречат гипотезе о наличии линейной корреляционной зависимости.